HDU 5963(游戏 博弈+规律)

题意是：

一群男生和一群女生玩游戏：给出一棵 n 个节点的树，这棵树的每条边有一个权值 0 或 1。 在一局游戏开始时，确定一个节点作为根。从女生开始，双方轮流进行操作。

当一方操作时，要先选择一个不为根且到其父亲的边权为 1 的点，然后找出这个点到根节点的简单路径，将路径上所有边的权值翻转（即 0 变成 1，1 变成 0 )。

当一方无法操作时（即所有边的边权均为 0），另一方就获得了胜利。双方均采用最优策略，若女生获胜，则输出 “Girls win!”，否则输出“Boys win!”。

每局之间可能会有修改边权的操作，且每局游戏指定的根节点也可能是不同的。

开始时以为会很麻烦，借鉴了别人的博客，才想到修改边权只能每次修改一条边的，有了一些思路：

首先要明确结果只有两种，当操作数为奇数时女生获胜，当操作数为偶数时男生获胜。

一、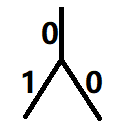 这种情况下需要经过两次操作才能将所有权值置 0 ；二、 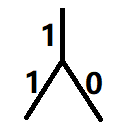这种情况下需要经过一次或三次操作才能将所有权值置 0 ；

三、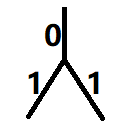这种情况下需要经过两次或四次操作才能将所有权值置 0 ；四、 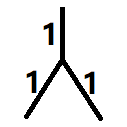这种情况下需要经过三次或五次操作才能将所有权值置 0。

上述四种情况的结论是只要进行操作就一定会出现的，不一定要特别采用最优策略，也就是说情况出现后先手与后手的输赢已经确定，双方只要按规则操作即使想可以改变结果也

无法做到，其实应该还有第五种情况，就是都为 0 的情况，这种情况下需要零次操作才能将所有权值置 0。

发现，当与根结点相连的边权和为偶数时需要且一定经过偶数次操作才能将所有权值置 0，当与根结点相连的边权和为奇数时需要且一定经过奇数次操作才能将所有权值置 0。

开始时打算用 40000*40000 的 bool 数组去存，但还是超内存了……

错误代码：

 #include <bits/stdc++.h>
 using namespace std;
 bool p[][];
 int main()
 {
     int t,n,m,x,y,z;
     scanf("%d",&t);
     while(t--)
     {
         scanf("%d%d",&n,&m);
         memset(p,,sizeof(p));
         for(int i = ; i < n; ++i)
         {
             scanf("%d%d%d",&x,&y,&z);
             p[x][y] = z;
             p[y][x] = z;
         }
         for(int i = ; i < m; ++i)
         {
             scanf("%d",&z);
             if(z)
             {
                 scanf("%d%d%d",&x,&y,&z);
                 p[x][y] = z;
                 p[y][x] = z;
             }
             else
             {
                 scanf("%d",&z);
                 x = ;
                 for(int i = ; i < ; ++i)
                     if(p[z][i]) ++x;
                 if(x&) puts("Girls win!");
                 else puts("Boys win!");
             }
         }
     }
     return ;
 }

改成 vector 数组才过了

代码如下：

 #include <bits/stdc++.h>
 using namespace std;
 vector<int> p[];
 int num[];
 int main()
 {
     int t,x,y,z,n,m;
     scanf("%d",&t);
     while(t--)
     {
         scanf("%d%d",&n,&m);
         memset(num,,sizeof(num));
         memset(p,,sizeof(p));
         for(int i = ; i < n; ++i)
         {
             scanf("%d%d%d",&x,&y,&z);
             if(z)
             {
                 ++num[x];
                 ++num[y];
                 p[x].push_back(y);
                 p[y].push_back(x);
             }
         }
         for(int i = ; i < m; ++i)
         {
             scanf("%d",&z);
             if(z)
             {
                 scanf("%d%d%d",&x,&y,&z);
                 vector<int>::iterator it1 = find(p[x].begin(),p[x].end(),y);
                 vector<int>::iterator it2 = find(p[y].begin(),p[y].end(),x);
                 if(it1!=p[x].end() && z==)
                 {
                     --num[x];
                     --num[y];
                     p[x].erase(it1);
                     p[y].erase(it2);
                 }
                 if(it1==p[x].end() && z==)
                 {
                     ++num[x];
                     ++num[y];
                     p[x].push_back(y);
                     p[y].push_back(x);
                 }
             }
             else
             {
                 scanf("%d",&z);
                 if(num[z]&) puts("Girls win!");
                 else puts("Boys win!");
             }
         }
     }
     return ;
 }

感谢这篇博客的作者：

https://blog.csdn.net/song_4/article/details/53063309