经典算法 KMP算法详解

内容：

1、问题引入

2、暴力求解方法

3、优化方法

4、KMP算法

1、问题引入

原始问题：

对于一个字符串 str （长度为N）和另一个字符串 match （长度为M），如果 match 是 str 的子串，

请返回其在 str 第一次出现时的首字母下标，若 match 不是 str 的子串则返回 -1

注：子序列和子串的区别：子序列可以不连续，子串必须连续

2、暴力求解方法

暴力求解方法：将 str 从头开始遍历并与 match 逐次比较，若碰到了不匹配字母则终止此次遍历转而从 str 的 第二个字符开始遍历

并与 match 逐次比较，直到某一次的遍历每个字符都与 match 匹配否则返回 -1 。易知此种 做法的时间复杂度为 O(N*M)

注：KMP算法则给出求解该问题时间复杂度控制在 O(N) 的解法

3、优化方法

优化方法：借助next数组进行优化

在一个字符串中，每个字符之前的最长前缀和最长后缀的最大匹配长度就是next数组中的值，next数组在KMP算法中的目的就是决定下次匹配对象

注：前缀不能包含最后一个字符，后缀也不能包含第一个字符(前缀和后缀不能是字符串整体!)

next数组示例：

• 字符串为abcabcd，此时d位置上的next数组值就是3
• 字符串为aaaaab，此时b位置上的next数组值就是4
• 字符串为ababac，此时next数组值依次是-1、0、0、1、2、3

如何求next数组：

当串 match 长度 mlen=1 时，规定 next[0]=-1 。当 mlen=2 时，去掉 match[1] 之后只剩下 match[0] ，

大匹配子串长度为0（因为前缀子串不能包含串尾字符，后缀子串不能包含串首字符），即 next[1]=0

而当 mlen>2 时， next[n] （n>=2）都可以推算出来：

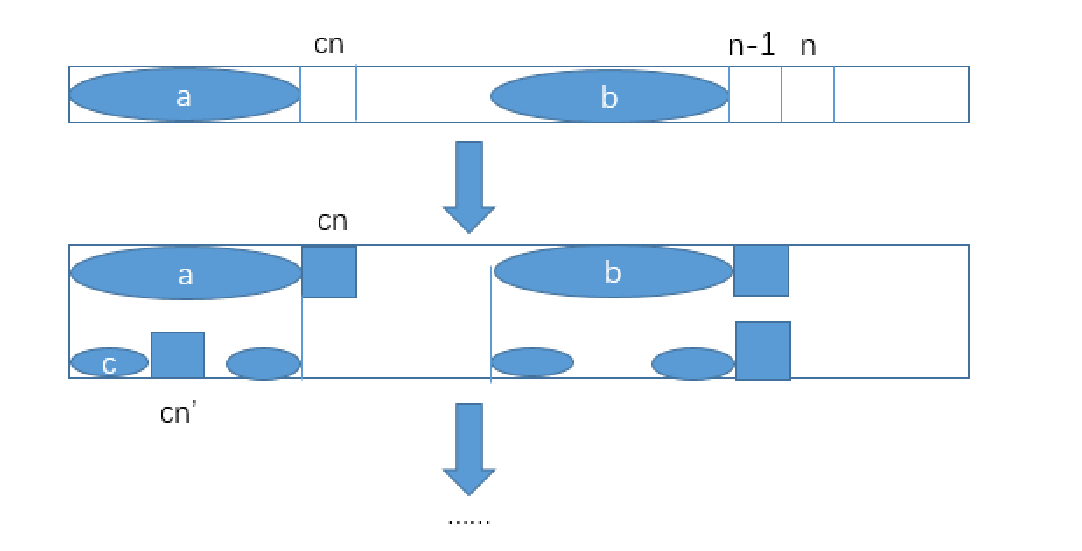
如上图所示，如果我们知道了next[n-1] ，那么 next[n] 的求解有两种情况：如果 match[cn]=match[n-1] ，

那么由a区域与b区域（a、b为最大匹配前缀子串和后缀字串）相同可知 next[n]=next[n1]+1 ；

如果 match[cn]!=match[n-1] ，那么求a区域中下一个能和b区域后缀子串中匹配的较大的一个，

即a区域 的大匹配前缀字串 c区域 ，将 match[n-1] 和c区域的后一个位置（ cn' ）上的字符比较，

如果相等则 next[n] 等于c区域的长度+1，而c区域的长度就是 next[cn] （ next数组的定义如此）；

如果不等则将 cn 打 到 cn' 的位置继续和 match[n-1] 比较，直到 cn 被打到 0 为止（即next[cn]=-1 为止），那么此时next[n]=0

求next数组代码：

     public static int[] getNextArray(char[] str) {
         if (str.length == 1) {
             return new int[] { -1 };
         }
         int[] next = new int[str.length];
         next[0] = -1;
         next[1] = 0;
         int i = 2;
         int cn = 0;
         while (i < next.length) {
             if (str[i - 1] == str[cn]) {
                 next[i++] = ++cn;
             } else if (cn > 0) {
                 cn = next[cn];
             } else {
                 next[i++] = 0;
             }
         }
         return next;
     }

4、KMP算法

KMP算法的原理如下：

子串 match 的 next数组找到之后就可以进行 KMP 算法求解此问题了。 KMP 算法的逻辑是对于 str 的 i~(i+k) 部分 （ i 、 i+k 合法）

和 match 的 0~k 部分（ k合法），如果有 str[i]=match[0] 、 str[i+1]=match[1] …… str[i+k-1]=match[k-1] ，但 str[i+k]!=[k] ，

那么 str 的 下标不用从i+k 变为 i+1 重新比较，只需将子串 str[0]~str[i+k-1] 的大匹配前缀子串的后一个字符 cn 重新与 str[i+k] 向后依次比较，

后面如果又遇到了不匹配的字符重复此操作即可：

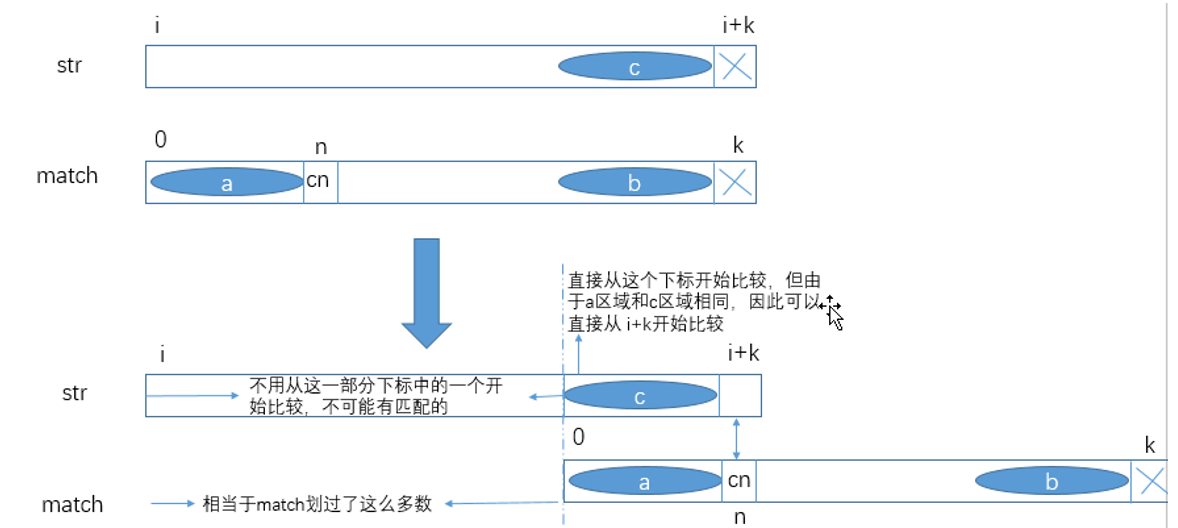
当遇到不匹配字符时，常规的做法是将 str 的遍历下标 sIndex 移到 i+1 的位置并将 match 的遍历下标 mIndex 移到 0 再依次比较，

这种做法并没有利用上一轮的比较信息（对下一轮的比较没有任何优化）；

而 KMP 算法则不是这样，当遇到不匹配的字符str[i+k] 和 match[k] 时， str 的遍历指针 sIndex=i+k 不用动，

将 match 右滑并将其遍历指针 mIndex 打到子串 match[0]~match[k-1]的最大匹配前缀子串的后一个下标 n 的位 置。

然后 sIndex 从 i+k 开始， mIndex 从 n 开始，依次向后比较，若再遇到不匹配的数则重复此过程

KMP算法核心代码：

     public static int getIndexOf(String s, String m) {
         if (s == null || m == null || m.length() < 1 || s.length() < m.length()) {
             return -1;
         }
         char[] str1 = s.toCharArray();
         char[] str2 = m.toCharArray();
         int i1 = 0;
         int i2 = 0;
         int[] next = getNextArray(str2);
         while (i1 < str1.length && i2 < str2.length) {
             if (str1[i1] == str2[i2]) {
                 i1++;
                 i2++;
             } else if (next[i2] == -1) {
                 i1++;
             } else {
                 i2 = next[i2];
             }
         }
         return i2 == str2.length ? i1 - i2 : -1;
     }

可以发现 KMP 算法中 str 的遍历指针并没有回溯这个动作（只向后移动），当完成匹配时 sIndex 的移动次数小 于 N ，

否则 sIndex 移动到串尾也会终止循环，所以 while 对应的匹配过程的时间复杂度为 O(N) ( if(next[j] != -1){ j = next[j] } 的

执行次数只会是常数次，因此可以忽略)

完整的KMP代码及测试样例如下：

 // KMP算法
 public class KMP {
     public static int getIndexOf(String s, String m) {
         if (s == null || m == null || m.length() < 1 || s.length() < m.length()) {
             return -1;
         }
         char[] str1 = s.toCharArray();
         char[] str2 = m.toCharArray();
         int i1 = 0;
         int i2 = 0;
         int[] next = getNextArray(str2);
         while (i1 < str1.length && i2 < str2.length) {
             if (str1[i1] == str2[i2]) {
                 i1++;
                 i2++;
             } else if (next[i2] == -1) {
                 i1++;
             } else {
                 i2 = next[i2];
             }
         }
         return i2 == str2.length ? i1 - i2 : -1;
     }

     public static int[] getNextArray(char[] str) {
         if (str.length == 1) {
             return new int[] { -1 };
         }
         int[] next = new int[str.length];
         next[0] = -1;
         next[1] = 0;
         int i = 2;
         int cn = 0;
         while (i < next.length) {
             if (str[i - 1] == str[cn]) {
                 next[i++] = ++cn;
             } else if (cn > 0) {
                 cn = next[cn];
             } else {
                 next[i++] = 0;
             }
         }
         return next;
     }

     public static void main(String[] args) {
         System.out.println(getIndexOf("abcabcababaccc", "ababa"));
         System.out.println(getIndexOf("just a test", "test"));
         System.out.println(getIndexOf("justatest", "test"));
         System.out.println(getIndexOf("asfawfasdf", "666"));
         System.out.println(getIndexOf("absafasdcc", "ababa"));
     }
 }