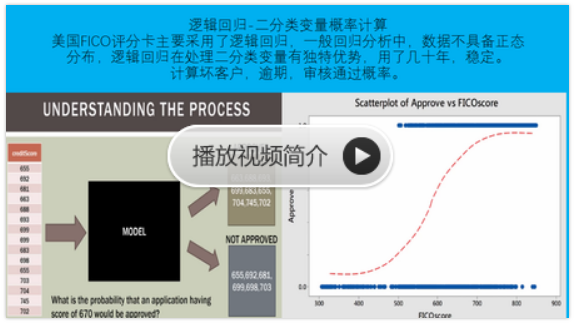
how to calculate the best fit to a plane in 3D, and how to find the corresponding statistical parameters

sklearn实战-乳腺癌细胞数据挖掘(博客主亲自录制视频教程)

https://study.163.com/course/introduction.htm?courseId=1005269003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share

 

 

# -*- coding: utf-8 -*-
'''
python入门/爬虫/人工智能/机器学习/自然语言/数据统计分析视频教程网址
https://pythoner.taobao.com/

https://github.com/thomas-haslwanter/statsintro_python/tree/master/ISP/Code_Quantlets/12_Multivariate/multipleRegression
Multiple Regression
- Shows how to calculate the best fit to a plane in 3D, and how to find the
  corresponding statistical parameters.
- Demonstrates how to make a 3d plot.
- Example of multiscatterplot, for visualizing correlations in three- to
  six-dimensional datasets.
'''
# Import standard packages
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns

# additional packages
import sys
import os
sys.path.append(os.path.join('..', '..', 'Utilities'))

try:
# Import formatting commands if directory "Utilities" is available
    from ISP_mystyle import showData 

except ImportError:
# Ensure correct performance otherwise
    def showData(*options):
        plt.show()
        return

# additional packages ...
# ... for the 3d plot ...
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm

# ... and for the statistic
from statsmodels.formula.api import ols

def generateData():
    ''' Generate and show the data: a plane in 3D '''
    #随机产生101个数据，取值范围从（-5到5）
    x = np.linspace(-5,5,101)
    (X,Y) = np.meshgrid(x,x)
    # To get reproducable values, I provide a seed value
    np.random.seed(987654321)
    #np.random.randn产生随机的正太分布数，np.shape(X)表示X的size（101,101）
    #np.random.randn(np.shape(X)[0], np.shape(X)[1])表示产生（101,101）个随机数
    Z = -5 + 3*X-0.5*Y+np.random.randn(np.shape(X)[0], np.shape(X)[1])

    # 绘图
    #Set the color
    myCmap = cm.GnBu_r
    # If you want a colormap from seaborn use:
    #from matplotlib.colors import ListedColormap
    #myCmap = ListedColormap(sns.color_palette("Blues", 20))

    # Plot the figure
    fig = plt.figure()
    ax = fig.gca(projection='3d')
    surf = ax.plot_surface(X,Y,Z, cmap=myCmap, rstride=2, cstride=2,
        linewidth=0, antialiased=False)
    ax.view_init(20,-120)
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    ax.set_zlabel('Z')
    fig.colorbar(surf, shrink=0.6)

    outFile = '3dSurface.png'
    showData(outFile)
    #X.flatten()把多维数据展开，弄成一维数据
    return (X.flatten(),Y.flatten(),Z.flatten())

def regressionModel(X,Y,Z):
    '''Multilinear regression model, calculating fit, P-values, confidence intervals etc.'''

    # Convert the data into a Pandas DataFrame
    df = pd.DataFrame({'x':X, 'y':Y, 'z':Z})

    # --- >>> START stats <<< ---
    # Fit the model
    model = ols("z ~ x + y", df).fit()
    # Print the summary
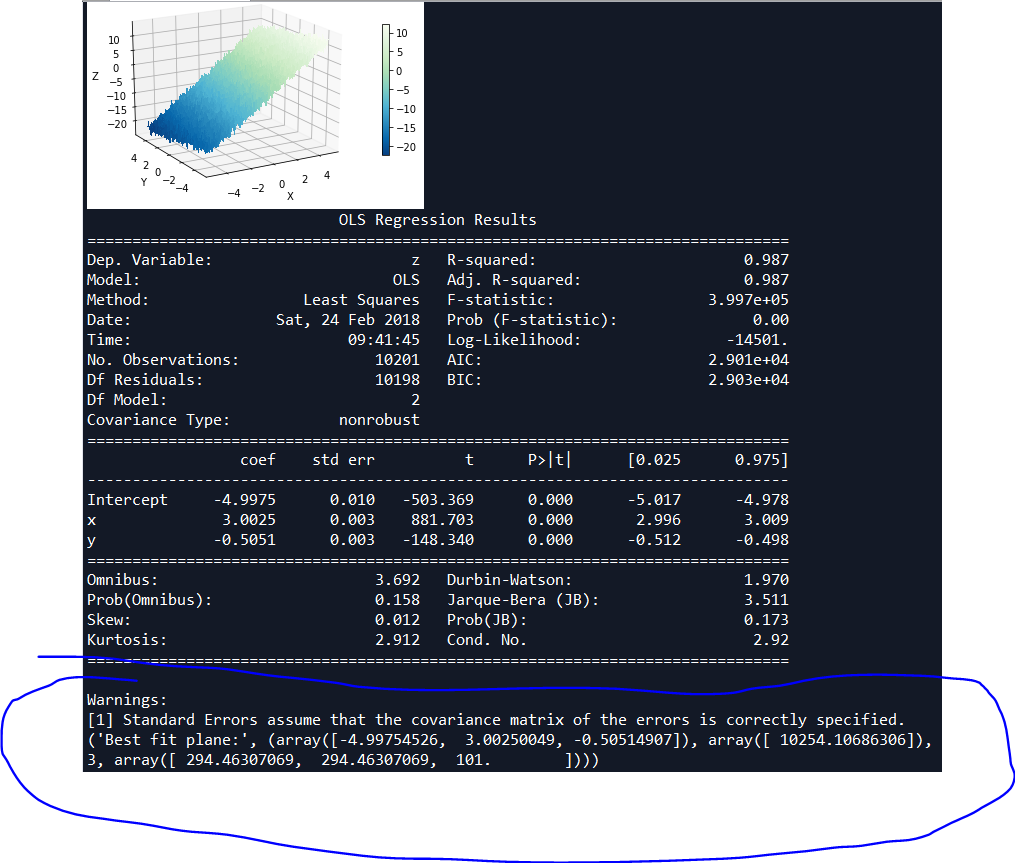
    print((model.summary()))
    # --- >>> STOP stats <<< ---
    return model._results.params  # should be array([-4.99754526,  3.00250049, -0.50514907])

#用numpy的线性回归模型，和上面regressionModel函数计算结果一致
def linearModel(X,Y,Z):
    '''Just fit the plane, using the tools from numpy'''

    # --- >>> START stats <<< ---
    M = np.vstack((np.ones(len(X)), X, Y)).T
    bestfit = np.linalg.lstsq(M,Z)
    # --- >>> STOP stats <<< ---
    print(('Best fit plane:', bestfit))
    return bestfit

if __name__ == '__main__':
    (X,Y,Z) = generateData()
    regressionModel(X,Y,Z)
    linearModel(X,Y,Z)

　　

 

 

python风控评分卡建模和风控常识(博客主亲自录制视频教程)

https://study.163.com/course/introduction.htm?courseId=1005214003&utm_campaign=commission&utm_source=cp-400000000398149&utm_medium=share