数据结构(六)查找---多路查找树(B树)
B 树
B树与B+树
一:定义
B树(B-树)是一种平衡的多路查找树。-3树和2--4树都是B树的特例。节点最大的孩子数组称为B树的阶(order),因此,-3树是3阶B树,--4树是4阶B树。
二:属性
一棵最小度为t的B树是满足如下四个条件的平衡多叉树:
1.每个节点最多包含2t−1个关键字;除根节点外的每个节点至少有t−1个关键字(t≤),根节点至少有一个关键字; 2.一个节点u中的关键字按非降序排列:u.key1≤u.key2≤…u.keynu.key1≤u.key2≤…u.keyn; 3.每个节点的关键字对其子树的范围分割。设节点uu有n+1个指针,指向其n+1棵子树,指针为u.p1,…u.pn,关键字ki为u.pi所指的子树中的关键字,有k1≤u.key1≤k2≤u.key2…k1≤u.key1≤k2≤u.key2…成立; 4.所有叶子节点处于同一层次。这表明B树是平衡的。平衡性其实正是B树名字的来源,B表示的正是单词Balanced;

比如说要查找7,首先从外存读取得到根节点3,,8三个元素,发现7不在,但是5、8之间,因此就通过A2再读取外存的6,7节点找到结束。 B树的插入和删除和2-3树、--4树类似。
三:用途
B树的数据结构为内外存的数据交互准备的
当要处理的数据很大时,无法一次全部装入内存。
这时对B树调整,使得B树的阶数与硬盘存储的页面大小相匹配。
比如说一棵B树的阶为1001(即1个节点包含1000个关键字),高度为2(从0开始),它可以存储超过10亿个关键字(1001x1001x1000+1001x1000+),
只要让根节点持久的保留在内存中,那么在这颗树上,寻找某一个关键字至多需要两次硬盘的读取即可。
四:性能
对于n个关键字的m阶B树,最坏情况查找次数计算
第一层至少1个节点,第二层至少2个节点,由于除根节点外每个分支节点至少有⌈m/⌉棵子树,则第三层至少有2x⌈m/⌉个节点...
这样第k+1层至少有2x(⌈m/⌉)^(k-),实际上,k+1层的节点就是叶子节点。
若m阶B树有n个关键字,那么当你找到叶子节点,其实也就等于查找不成功的节点为n+,
因此n+>=2x(⌈m/⌉)^(k-),即
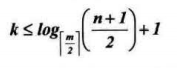
在含有n个关键字的B树上查找时,从根节点到关键字节点的路径上涉及的节点数不超多
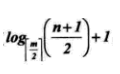
数据结构(六)查找---多路查找树(B树)的更多相关文章
- 数据结构(六)查找---多路查找树(B+树)
前提 下图B树,我们要遍历它,假设每个节点都属于硬盘的不同页面,我们为了中序遍历所有的元素,页面2-页面1-页面3-页面1-页面4-页面1-页面5.而且我们每经过节点遍历时,都会对节点中的元素进行一次 ...
- 数据结构(四十一)多路查找树(B树)
一.多路查找树的背景 前面所讨论的查找算法都是在内存中进行的,它们适用于较小的文件,而对于较大的.存放在外存储器上的文件就不合适了,对于此类大规模的文件,即使是采用了平衡二叉树,在查找效率上仍然较低. ...
- 多路查找树之2-3-4树和B树 - 数据结构和算法82
多路查找树之2-3-4树和B树 让编程改变世界 Change the world by program 由2-3树到2-3-4树 ...... 省略,具体请看视频讲解 ...... B树 一个m阶的B ...
- Java数据结构(十五)—— 多路查找树
多路查找树 二叉树和B树 二叉树的问题分析 二叉树操作效率高 二叉树需要加载到内存,若二叉树的节点多存在如下问题: 问题1:构建二叉树时,需多次进行I/O操作,对与速度有影响 问题2:节点海量造成二叉 ...
- 数据结构和算法学习笔记十五:多路查找树(B树)
一.概念 1.多路查找树(multi-way search tree):所谓多路,即是指每个节点中存储的数据可以是多个,每个节点的子节点数也可以多于两个.使用多路查找树的意义在于有效降低树的深度,从而 ...
- 【查找结构5】多路查找树/B~树/B+树
在前面专题中讲的BST.AVL.RBT都是典型的二叉查找树结构,其查找的时间复杂度与树高相关.那么降低树高自然对查找效率是有所帮助的.另外还有一个比较实际的问题:就是大量数据存储中,实现查询这样一个实 ...
- HTTP协议漫谈 C#实现图(Graph) C#实现二叉查找树 浅谈进程同步和互斥的概念 C#实现平衡多路查找树(B树)
HTTP协议漫谈 简介 园子里已经有不少介绍HTTP的的好文章.对HTTP的一些细节介绍的比较好,所以本篇文章不会对HTTP的细节进行深究,而是从够高和更结构化的角度将HTTP协议的元素进行分类讲 ...
- 二叉查找树、平衡二叉树(AVLTree)、平衡多路查找树(B-Tree),B+树
B+树索引是B+树在数据库中的一种实现,是最常见也是数据库中使用最为频繁的一种索引. B+树中的B代表平衡(balance),而不是二叉(binary),因为B+树是从最早的平衡二叉树演化而来的. 在 ...
- 多路查找树(2-3 树、2-3-4 树、B 树、B+ 树)
本文参考自<大话数据结构> 计算机中数据的存储 一般而言,我们都是在内存中处理数据,但假如我们要操作的数据集非常大,内存无法处理了,在这种情况下对数据的处理需要不断地从硬盘等存储设备中调入 ...
随机推荐
- Android WebView 文明踩坑之路
情景一 webview 以头布局的形式添加到 RecyclerView 中,第一次进入页面,当页面中有 EditText 并且点击时,甚至是类似点赞更换图片.点击 WebView 任意区域,都会造成 ...
- Gradle vs Maven Comparison
https://gradle.org/maven-vs-gradle/ Maven需要搭建本地仓库:Gradle直接集成了仓库. ??? 从Maven转移到Gradle,对于如何使用类似于Maven的 ...
- [转帖]看完这篇文章你还敢说你懂JVM吗?
看完这篇文章你还敢说你懂JVM吗? 在一些物理内存为8g的服务器上,主要运行一个Java服务,系统内存分配如下:Java服务的JVM堆大小设置为6g,一个监控进程占用大约 600m,Linux自身使用 ...
- PSexec以及xcopy的简单使用
1. 远程执行命令. 有时候不想远程但是想执行一些命令, 比较简单的方法是: 下载systeminternals 然后解压缩后可以讲目录放到path环境变量中 然后打开命令行工具 输入 如下的命令 p ...
- const修饰符与函数
一.用const修饰函数的参数 函数参数类型前加const指明该参数为常量,在函数内部不可改变. void func(const int x) { //x不可以在内部进行赋值等操作. } 注:当参数为 ...
- 使用ssh tunnel 来做代理或跳板
接前文 http://www.cnblogs.com/piperck/p/6188984.html 使用ssh config配置文件来管理ssh连接 前文说了如何配置自己的ssh config 来方 ...
- LinkedList 实现 Queue
package cn.com.example; import java.util.LinkedList; /** * Created by Jack on 2017/3/8. */ public cl ...
- 使用nmon进行系统监控
一.下载并安装: 下载地址:http://nmon.sourceforge.net/pmwiki.php?n=Site.Download 下载版本:nmon16g_x86.tar.gz 不用的Li ...
- 封装caffe版的deeplab为库供第三方使用
1.解决deeplab编译问题 http://m.2cto.com/kf/201612/579545.html
- maven 父工程 消除重复 对子模块进行管理 主要继承依赖
子类继承父类的 可以不需要groupid与versionid
