点云NDT配准方法介绍

三维配准中经常被提及的配准算法是ICP迭代的方法，这种方法一般般需要提供一个较好的初值，也就是需要粗配准，同时由于算法本身缺陷，最终迭代结果可能会陷入局部最优，导致配准失败，往往达不到我们想要的效果。本文介绍的是另一种比较好的配准算法，NDT配准。所谓NDT就是正态分布变换，作用与ICP一样用来估计两个点云之间的刚体变换。用标准最优化技术来确定两个点云间的最优的匹配，因为其在配准过程中不利用对应点的特征计算和匹配，所以时间比其他方法快。这个配准算法耗时稳定，跟初值相关不大，初值误差大时，也能很好的纠正过来。

对比ICP配准方法需要提出不合适的点对，比如点对之间距离过大，包含了边界点对，每次迭代都要搜索最近点，计算代价较大。正态分布变换（NDT）算法是一种很有用途的点云配准方法，是一个一次性初始化工作，不需要消耗大量的代价计算最近邻搜索匹配点，并且概率密度函数在两幅图像采集之间的额时间可以离线计算出来，但仍在存在的问题很多，包括收敛域差、NDT代价函数的不连续性以及稀疏室外环境下不可靠的姿态估计等。

具体关于两种方法的对比可查看文献：http://www.diva-portal.org/smash/get/diva2:276162/FULLTEXT02.pdf

那么针对无损检测算法在二维和三维场景下的不足，也会有研究者们提出了相应的解决方法。为了改进二维扫描配准的无损检测收敛域，提出了一种多尺度K均值无损检测（MSKM-NDT）算法，利用K均值聚类对二维点云进行分割，并对多尺度聚类进行扫描配准优化。与标准无损检测算法相比，k-均值聚类方法生成的高斯分布更少，从而可以评估所有高斯聚类的成本函数，从而保证算法的收敛性。由于K均值聚类不能很好地扩展到三维，提出了分段贪婪聚类无损检测（SGC-NDT）方法，作为一种改进和保证三维点云收敛的替代方法，该点云包含与环境地面相对应的点。SGC-NDT算法使用高斯过程回归模型分割接地点，并使用贪婪方法对非接地点进行聚类。区域增长聚类算法提取环境中的自然特征，生成高斯聚类，在无损检测框架内用于扫描配准。涉及到的相关文献如下：

Das A, Waslander SL. Scan Registration using Segmented Region Growing NDT. International Journal of Robotics Research. 2014.

Das A, Servos J, Waslander SL. 3D Scan Registration Using the Normal Distributions Transform with Ground Segmentation and Point Cloud Clustering. In 2013 IEEE International Conference on Robotics and Automation. Karlsruhe, Germany; 2013.

Das A, Waslander SL.Scan Registration with Multi-Scale K-Means Normal Distributions Transform. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Villamoura, Portugal; 2012.

 

那么接下里就具体介绍一下NDT算法的步骤

（1）该算法的第一步是将扫描占用的空间细分为单元格网格（2D图像中的正方形或3D中的立方体），基于单元内的点分布计算每个单元的PDF。 每个单元格中的PDF可以解释为单元格内表面点x^的生成过程。将点云投票到各个格子中，计算每个格子的PDF，PDF可以当做表面的近似表达，协方差矩阵的特征向量和特征值可以表达表面信息（朝向、平整度） 格子内少于3个点，经常会协方差矩阵不存在逆矩阵，所以只计算点数大于5的cell，涉及到下采样方法。

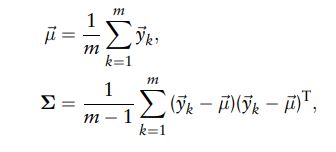
正态分布给出了点云的分段平滑表示，具有连续导数。 每个PDF都可以看作是局部表面的近似值，描述了表面的位置以及它的方向和平滑度。 2D激光扫描及其相应的正态分布如图6.1所示。 图6.2显示了矿井隧道扫描的3D正态分布。

由于目前的工作主要集中在正态分布上，让我们更仔细地研究单变量和多变量正态分布的特征。 在一维情况下，正态分布的随机变量x具有一定的期望值μ，并且关于该值的不确定性用方差σ表示。

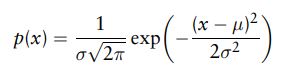
在多维的情况下，平均值和方差由平均向量 μ和协方差来描述矩阵Σ。 协方差矩阵的对角元素表示方差每个变量，非对角线元素表示的是协方差变量。 图6.3说明了一维，二维和三维的正态分布

（2）将第二幅扫描点云的每个点按转移矩阵T的变换。

(3)第二幅扫描点落于参考帧点云的哪个 格子，计算响应的概率分布函数

（4）当使用NDT进行扫描点配准时，目标是找到当前扫描点的位姿，以最大化当前扫描的点位于参考扫描表面上的可能性，该位姿是要优化的参数; 也就是说，当前扫描的点云估计的旋转和平移向量。求所有点的最优值，目标函数为

 

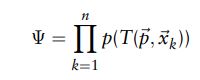
2D-NDT

对于2D配准，有三个要优化的转换参数。 让p = [tx，ty，φ]T，其中 tx 和 ty 是平移参数，φ是旋转角度。 使用逆时针旋转，2D变换功能是

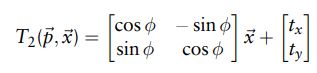
3D-NDT

NDT的2D和3D配准的主要区别在于空间变换函数T（ p， x）及其偏导数。3D NDT使用欧拉角，有六个转换要优化的参数：三个用于平移，三个用于旋转。

可以使用六维参数矢量对姿势进行编码 p6 = [tx，ty，tz，φx，φy，φz]T

使用欧拉序列z-y-x，3D变换函数是

更具体的解释可查看文献

在PCL中给出的NDT例子如下

http://pointclouds.org/documentation/tutorials/normal_distributions_transform.php#normal-distributions-transform