[蓝桥杯]ALGO-185.算法训练_Trash Removal

题目描述：

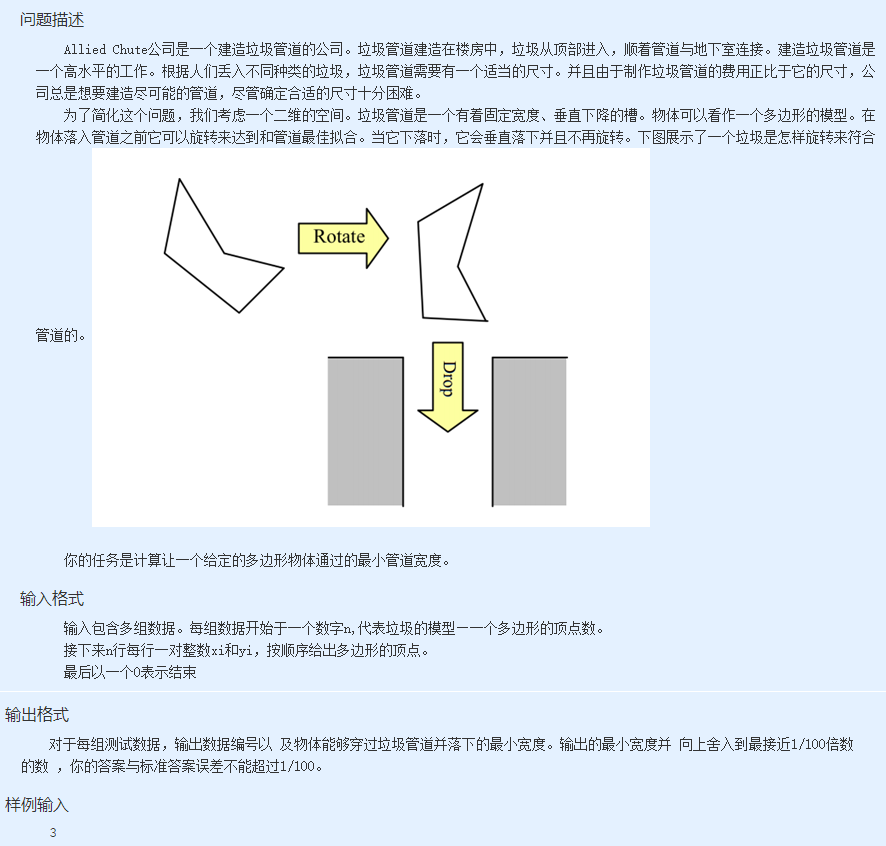
代码如下：

 #include <algorithm>
 #include <cstdio>
 #include <cstdlib>
 #include <cmath>
 #include <cstring>
 #include <iostream>
 #define INF 0x7fffffff
 using namespace std;

 typedef long long LL;
 const int N =  + ;
 const double PI = acos(-1.0);
 const double esp = 1e-;

 int dcmp(double x) {if(fabs(x) < esp) return ; else return x<?-:;}

 struct Point
 {
     double x,y;
     Point(double x=,double y=):x(x),y(y){ }
 };

 typedef Point Vector;

 Vector operator + (Vector A, Vector B) {return Vector(A.x+B.x, A.y+B.y);}
 Vector operator - (Vector A, Vector B) {return Vector(A.x-B.x, A.y-B.y);}
 Vector operator * (Vector A, double p) {return Vector(A.x*p, A.y*p);}
 Vector operator / (Vector A, double p) {return Vector(A.x/p, A.y/p);}
 bool operator < (const Point& a, const Point& b){ return a.x<b.x || (a.x==b.x && a.y<b.y);}
 bool operator == (const Point& a, const Point& b){return dcmp(a.x-b.x)== && dcmp(a.y-b.y)==;}

 double Dot(Vector A, Vector B){ return A.x*B.x+A.y*B.y; }
 double Length(Vector A){return sqrt(Dot(A, A));}            //计算向量的模
 double Angle(Vector A, Vector B) {return acos( Dot(A, B)/Length(A)/Length(B) );}//计算两向量的角度 

 double Cross(Vector A, Vector B) { return A.x*B.y - A.y*B.x ;}        //计算两向量的叉积
 double Area2(Point A, Point B, Point C){return Cross(B-A, C-A); }    //三点形成的两向量 

 double DistanceToLine(Point P, Point A, Point B)    //计算以AB为底边的高
 {
     Vector v1 = B-A, v2 = P-A;
     return fabs(Cross(v1, v2)) / Length(v1);
 }
 int ConvexHull(Point *p, int n, Point *ch)
 {
     sort(p,p+n);    //排序各顶点
     int m = ;
     for(int i=;i<n;i++)    //维护凸壳
     {
         while(m> && Cross(ch[m-]-ch[m-], p[i]-ch[m-]) <= ) m--;
         ch[m++] = p[i];        //记录凸壳的顶点
     }
     int k = m;    //记录凸壳顶点数
     for(int i = n- ;i>=;i--)    //除去底边的两个顶点
     {
         while(m>k && Cross(ch[m-]-ch[m-], p[i]-ch[m-]) <= ) m--;
         ch[m++] = p[i];
     }
     if(n > ) m--;
     return m;
 }

 int n;
 Point P[N],ch[N];

 int main()
 {
     int C=;
     while(scanf("%d",&n)!=EOF && n)    //输入多边形的边数
     {
         for(int i=;i<n;i++)
         {
             scanf("%lf%lf",&P[i].x,&P[i].y);//记录各点的坐标
         }
         int m=ConvexHull(P,n,ch);    //得到该多边形的凸壳顶点数
         double ans = 1e20;            //用于记录最小宽度
         for(int i=;i<=m;i++)        //枚举凸壳的顶点
         {
             double max_dis = ;        //用于记录各底边的高
             for(int j=;j<m;j++)    //确定底边后，查找其对应的高，并记录最大值
             {
                 max_dis = max(max_dis, DistanceToLine(ch[j],ch[i%m],ch[i-]));
             }
             ans = min(ans, max_dis);//最小宽度即为最大高度
         }
         ans = ceil(ans * ) / 100.0;

         printf("Case %d: %.2lf\n",C++, ans);
     }

     return ;
 }

C++解法

解题思路：

该题使用了几何计算中的凸边算法（什么是凸边：https://blog.csdn.net/HouszChina/article/details/79251474）

首先对输入多边形的点进行凸壳维护，得到凸壳的点集

然后枚举底边，计算对应的高，并保留最大的高度(即题目要求的最小宽度)