代码本色 用编程模拟自然系统 (Daniel Shiffman 著)
https://cdnjs.cloudflare.com/ajax/libs/p5.js/0.5.7/p5.js
http://github.com/shiffman/PBox2D
第0章 引言 (已看)
第1章 向量 (已看)
第2章 力 (已看)
第3章 震荡 (已看)
第4章 粒子系统 (已看)
第5章 物理函数库 (已看)
第6章 自治智能体 (已看)
第7章 细胞自动机 (已看)
第8章 分形 (已看)
第9章 代码的进化 (已看)
第10章 神经网络 (已看)
第0章 引言
0.1 随机游走
0.2 随机游走类

Walker w;
void setup() {
size(,);
w = new Walker();
background();
}
void draw() {
w.step();
w.display();
}
class Walker {
int x;
int y;
Walker() {
x = width / ;
y = height / ;
}
void display() {
stroke();
point(x,y);
}
void step() {
));
) {
x++;
} ) {
x--;
} ) {
y++;
} else {
y--;
}
}
}
0.3 概率和非均匀分布

int[] randomCounts;
void setup() {
size(,);
randomCounts = ];
}
void draw() {
background();
int index = int(random(randomCounts.length));
randomCounts[index]++;
stroke();
fill();
int w = width / randomCounts.length;
; x < randomCounts.length; x++) {
rect(x * w,height - randomCounts[x],w - ,randomCounts[x]);
}
}

Walker w;
void setup() {
size(,);
w = new Walker();
background();
}
void draw() {
w.step();
w.display();
}
class Walker {
int x;
int y;
Walker() {
x = width / ;
y = height / ;
}
void display() {
stroke();
point(x,y);
}
void step() {
);
if(r < 0.4) {
x++;
} else if(r < 0.6) {
x--;
} else if(r < 0.8) {
y++;
} else {
y--;
}
}
}
0.4 随机数的正态分布

import java.util.Random;
Random generator;
void setup() {
size(,);
generator = new Random();
}
void draw() {
float num = (float)generator.nextGaussian();
;
;
float x = sd * num + mean;
noStroke();
fill(,);
ellipse(x,,,);
}
0.5 自定义分布的随机数
0.6 Perlin噪声(一种更p平滑的算法)
0.6.1 映射噪声

;
void setup() {
size(,);
}
void draw() {
float n = noise(t);
,,,width);
ellipse(x,,,);
t += 0.01;
}
0.6.2 二维噪声

// Daniel Shiffman
// The Nature of Code
// http://www.shiffman.net/
float increment = 0.01;
// The noise function's 3rd argument, a global variable that increments once per cycle
float zoff = 0.0;
// We will increment zoff differently than xoff and yoff
float zincrement = 0.02;
void setup() {
size(,);
}
void draw() {
background();
// Optional: adjust noise detail here
// noiseDetail(8,0.65f);
loadPixels();
float xoff = 0.0; // Start xoff at 0
// For every x,y coordinate in a 2D space, calculate a noise value and produce a brightness value
; x < width; x++) {
xoff += increment; // Increment xoff
float yoff = 0.0; // For every xoff, start yoff at 0
; y < height; y++) {
yoff += increment; // Increment yoff
// Calculate noise and scale by 255
;
// Try using this line instead
//float bright = random(0,255);
// Set each pixel onscreen to a grayscale value
pixels[x+y*width] = color(bright,bright,bright);
}
}
updatePixels();
zoff += zincrement; // Increment zoff
}
0.7 前进
第1章 向量
1.1 向量
向量(Euclidean vector,以希腊数学家欧几里得的名字命名,也称作几何向量),它的定义是:一个既有大小又有方向的几何对象

;
;
;
float yspeed = 3.3;
void setup() {
size(,);
smooth();
background();
}
void draw() {
//background(255);
x = x + xspeed;
y = y + yspeed;
)) {
xspeed = xspeed * -;
}
)) {
yspeed = yspeed * -;
}
stroke();
fill();
ellipse(x,y,,);
}
1.2 Processing中的向量
对每一帧动画:新位置 = 当前位置在速度作用下的位置
如果速度是一个向量(两点之间的差异),那位置是否也是一个向量?从概念上来说,有人会争论说位置并不是向量,因为它没有描述从某个点到另一个点的移动,它只描述了空间中的一个点而已.
然而,对于位置这个概念,另一种描述是从原点到该位置的移动路径.因此位置也可以用一个向量表示,它代表原点与该位置的差异

1.3 向量的加法
PVector location;
PVector velocity;
void setup() {
size(,);
location = ,);
velocity = );
}
void draw() {
background();
location.add(velocity);
)) {
velocity.x = velocity.x * -;
}
)) {
velocity.y = velocity.y * -;
}
stroke();
fill();
ellipse(location.x,location.y,,);
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
}
1.4 更多的向量运算
1.4.1 向量的减法
PVector location;
PVector velocity;
void setup() {
size(,);
}
void draw() {
background();
PVector mouse = new PVector(mouseX,mouseY);
PVector center = ,height / );
mouse.sub(center);
translate(width / ,height / );
line(,,mouse.x,mouse.y);
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
}
1.4.2 向量加减法的运算律
1.4.3 向量的乘法
1.4.4 更多的向量运算符
1.5 向量的长度
1.6 单位化向量

PVector location;
PVector velocity;
void setup() {
size(,);
}
void draw() {
//background(255);
PVector mouse = new PVector(mouseX,mouseY);
PVector center = ,height / );
mouse.sub(center);
mouse.normalize();
mouse.mult();
translate(width / ,height / );
line(,,mouse.x,mouse.y);
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
}
1.7 向量的运动:速度
Mover mover;
void setup() {
size(,);
mover = new Mover();
}
void draw() {
background();
mover.update();
mover.checkEdges();
mover.display();
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
}
class Mover {
PVector location;
PVector velocity;
Mover() {
location = new PVector(random(width),random(height));
velocity = ,),random(-,));
}
void update() {
location.add(velocity);
}
void display() {
stroke();
fill();
ellipse(location.x,location.y,,);
}
void checkEdges() {
if(location.x > width ) {
location.x = ;
} ) {
location.x = width;
}
if(location.y > height) {
location.y = ;
} ) {
location.y = height;
}
}
}
1.8 向量的运动:加速度
Mover mover;
void setup() {
size(,);
mover = new Mover();
}
void draw() {
background();
mover.update();
mover.checkEdges();
mover.display();
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
}
class Mover {
PVector location;
PVector velocity;
PVector acceleration;
float topspeed;
Mover() {
location = new PVector(random(width),random(height));
velocity = ,);
acceleration = new PVector(-0.001,0.01);
topspeed = ;
}
void update() {
velocity.add(acceleration);
velocity.limit(topspeed);
location.add(velocity);
println(velocity.mag());
}
void display() {
stroke();
fill();
ellipse(location.x,location.y,,);
}
void checkEdges() {
if(location.x > width ) {
location.x = ;
} ) {
location.x = width;
}
if(location.y > height) {
location.y = ;
} ) {
location.y = height;
}
}
}
1.9 静态函数和非静态函数
1.10 加速度的交互
Mover[] movers = ];
void setup() {
size(,);
background();
; i < movers.length; i++) {
movers[i] = new Mover();
}
}
void draw() {
background();
; i < movers.length; i++) {
movers[i].update();
movers[i].checkEdges();
movers[i].display();
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
println(mag());
}
}
}
class Mover {
PVector location;
PVector velocity;
PVector acceleration;
float topspeed;
Mover() {
location = new PVector(random(width),random(height));
velocity = ,);
topspeed = ;
}
void update() {
PVector mouse = new PVector(mouseX,mouseY);
mouse.sub(location);
PVector dir = mouse;
dir.normalize();
dir.mult(0.5);
acceleration = dir;
velocity.add(acceleration);
velocity.limit(topspeed);
location.add(velocity);
}
void display() {
stroke();
fill();
ellipse(location.x,location.y,,);
}
void checkEdges() {
if(location.x > width ) {
location.x = ;
} ) {
location.x = width;
}
if(location.y > height) {
location.y = ;
} ) {
location.y = height;
}
}
}
第2章 力
2.1 力和牛顿运动定律
力是一个向量,它使有质量的物体产生加速
2.1.1 牛顿第一运动定律
牛顿第一运动定律简述为:物体有保持禁止或运动的趋势
加上外力的作用,牛顿第一运动定律可以扩展为:除非有不均衡外力的作用,否则物体始终保持静止或匀速直线运动状态.
在Processing中,我们可以这样表述牛顿第一运动定律:在平衡状态下,对象的速度向量(PVector对象)始终都是常量
2.1.2 牛顿第三运动定律
牛顿第三运动定律通常表述为:每个作用力都有一个大小相等,方向相反的反作用力
牛顿第三运动定律的更好表述是:力总是成对出现,且这两个力大小相等,方向相反
这个表述仍然会引起误解,因为它看起来像是说:成对出现的力总是会相互取消,事实并不是这样,成对出现的力并不是作用在同一个物体上.这两个力的大小相等,但并不意味着它们产生的运动效果也一样(或者物体会停止运动).
2.1.3 牛顿第三运动定律(从Processing的角度表述)
如果我们要计算一个由A施加在B上的作用力f(PVector对象),必须额外施加一个由B作用在A上的反作用力(对象PVector.mult(f,-1));
但是在用Processing编程模拟时,我们不一定要遵循上面的说法.举个例子,在模拟物体之间的引力时,我们确实需要同时计算作用力与反作用力.但在另一些场景中,比如模拟风力的效果时,我们就不需要计算物体作用在空气上的反作用力,因为我们根本不会去模拟空气.
记住,我们只是想从自然的物理学中吸取一点编程灵感,并不是完美精确地模拟一切事物
2.2 力和Processing的结合:将牛顿第二运动定律作为一个函数
牛顿的第二运动定律被表述为:力等于质量乘以加速度.用公式表示为:F = M * A; 另外一种写法: A = F / M;加速度和力成正比,和质量成反比
重量和质量
质量是物质量的度量(以千克为单位)
重量,通常被误认为质量,实际上指的是物体所受重力的大小.根据牛顿第二运动定律,重量等于质量乘以重力加速度(w = m * g).重量以"牛顿"为单位.
密度等于质量除以物体的体积(例如以"克/立方厘米"为单位)
假设所有对象的质量为1.根据A / 1 = F,我们有A = F;
物体的加速度等于力.这是一个好消息,因为我们在第1章看到加速度是控制物体运动的关键因素:位置由速度控制,而速度由加速度控制.加速度是一切运动的起因.根据上面的公式,现在力变成了运动的起因
// 同时拥有位置(location),速度(velocity)和加速度(acceleration)的Moverl
class Mover {
PVector location;
Pvector velocity;
Pvecotr acceleration;
// 牛顿第二定律最简单的实现方式
// 但是这是错的实现方式,后面的力会覆盖前面的力
void applyForce(PVector force) [
acceleration = force;
}
}
mover.applyForce(wind);
mover.applyForce(gravity);
2.3 力的累加
更准确的牛顿第二运动定律:合力等于质量乘以加速度,或者可以说成:加速度等于所有力的和除以质量.
我们不需要在程序中记录加速度,因为它是根据当时的外力计算出来的.在这一点上,加速度和位置截然不同,为了能在下一帧移动到正确的位置,我们必须记录物体上一帧的位置
mover.applyForce(wind);
mover.applyForce(gravity);
mover.update();
mover.display();
void applyForce(PVector force) {
// 将新的力添加而不是赋值到加速度上
acceleration.add(force);
}
if(mousePressed) {
PVector wind = );
mover.applyForce(wind);
}
void update() {
velocity.add(acceleration);
location.add(velocity);
acceleration.mult();
}
2.4 处理质量
度量单位
本书中,常用的度量单位是:像素("这两个圆相距100个像素")和动画帧数("这个圆的移动速率是每帧两个像素").
对于质量,程序世界里并没有合适的单位,只要你愿意,完全可以用任意单位表示.为了易于演示,将质量和像素结合在一起(比如质量为10的物体,绘制半径是10个像素).这么做能让我们对物体的质量有直观的认识.
class Mover {
PVector location;
PVector velocity;
PVector acceleration;
float mass;
Mover() {
location = new PVector(random(width),random(height));
velocity = ,);
acceleration = ,);
mass = 10.0;
}
// 错误
void applyForce(PVector force) {
force.div(mass);
acceleration.add(force);
}
// 正确
void applyForce(PVector force) {
PVector f = force.get();
f.div(mass);
acceleration.add(f);
}
}
2.5 制造外力

Mover m;
void setup() {
size(,);
m = new Mover();
}
void draw() {
//background(255);
PVector wind = );
PVector gravity = ,0.1);
m.applyForce(wind);
m.applyForce(gravity);
m.update();
m.display();
m.checkEdges();
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
println(mag());
}
}
}
class Mover {
PVector location;
PVector velocity;
PVector acceleration;
float mass;
Mover() {
location = ,);
velocity = ,);
acceleration = ,);
mass = ;
}
void applyForce(PVector force) {
PVector newVector = force.get();
newVector.div(mass);
acceleration.add(newVector);
}
void update() {
velocity.add(acceleration);
location.add(velocity);
acceleration.mult();
}
void display() {
stroke();
strokeWeight();
fill();
ellipse(location.x,location.y,,);
}
void checkEdges() {
if(location.x > width) {
location.x = width;
velocity.x *= -;
} ) {
velocity.x *= -;
location.x = ;
}
if(location.y > height) {
velocity.y *= -;
location.y = height;
}
}
}

Mover[] movers = ];
void setup() {
size(,);
; i < movers.length;i++) {
movers[i] = ),,);
}
}
void draw() {
//background(255);
; i < movers.length;i++) {
PVector wind = );
PVector gravity = ,0.1);
movers[i].applyForce(wind);
movers[i].applyForce(gravity);
movers[i].update();
movers[i].display();
movers[i].checkEdges();
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
println(mag());
}
}
}
class Mover {
PVector location;
PVector velocity;
PVector acceleration;
float mass;
color c;
Mover(float m,float x,float y) {
location = new PVector(x,y);
velocity = ,);
acceleration = ,);
mass = m;
c = color(random(),random(),random());
}
void applyForce(PVector force) {
PVector newVector = force.get();
newVector.div(mass);
acceleration.add(newVector);
}
void update() {
velocity.add(acceleration);
location.add(velocity);
acceleration.mult();
}
void display() {
stroke();
strokeWeight();
fill(c);
//fill(random(255),random(255),random(255));
ellipse(location.x,location.y,mass * ,mass * );
}
void checkEdges() {
if(location.x > width) {
location.x = width;
velocity.x *= -;
} ) {
velocity.x *= -;
location.x = ;
}
if(location.y > height) {
velocity.y *= -;
location.y = height;
}
}
}
2.6 地球引力和力的建模

Mover[] movers = ];
void setup() {
size(,);
; i < movers.length;i++) {
movers[i] = ),,);
}
}
void draw() {
//background(255);
; i < movers.length;i++) {
PVector wind = );
float m = movers[i].mass;
PVector gravity = ,0.1 * m);
movers[i].applyForce(wind);
movers[i].applyForce(gravity);
movers[i].update();
movers[i].display();
movers[i].checkEdges();
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
println(mag());
}
}
}
class Mover {
PVector location;
PVector velocity;
PVector acceleration;
float mass;
color c;
Mover(float m,float x,float y) {
location = new PVector(x,y);
velocity = ,);
acceleration = ,);
mass = m;
c = color(random(),random(),random());
}
void applyForce(PVector force) {
PVector newVector = force.get();
newVector.div(mass);
acceleration.add(newVector);
}
void update() {
velocity.add(acceleration);
location.add(velocity);
acceleration.mult();
}
void display() {
stroke();
strokeWeight();
fill(c);
//fill(random(255),random(255),random(255));
ellipse(location.x,location.y,mass * ,mass * );
}
void checkEdges() {
if(location.x > width) {
location.x = width;
velocity.x *= -;
} ) {
velocity.x *= -;
location.x = ;
}
if(location.y > height) {
velocity.y *= -;
location.y = height;
}
}
}
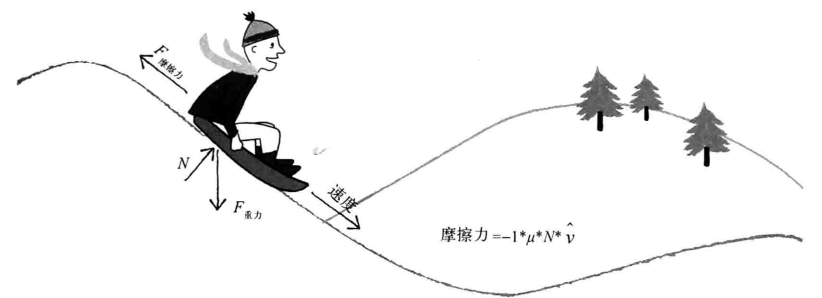
2.7 摩檫力
摩檫力是一种耗散力.耗散力的定义是:在运动中使系统总能量减少的力.比如说,开车时,脚踩刹车板会让车通过摩檫力使轮胎减速,在这个过程中,动能被转化为热能.只要两个物体的表面相互接触,它们之间就有摩檫力.摩檫力可分为静摩檫力(物体相对表面静止不动)和动摩檫力(物体在表面上运动)

Mover[] movers = ];
void setup() {
size(,);
randomSeed();
; i < movers.length;i++) {
movers[i] = ,),,);
}
}
void draw() {
background();
; i < movers.length;i++) {
PVector wind = );
PVector gravity = ,0.1 * movers[i].mass);
// 摩擦戏数
float c = 0.05;
// 正向力
;
PVector friction = movers[i].velocity.get();
friction.mult(-); // 乘以 -1
friction.normalize(); // 归一化
friction.mult(c); // 乘以摩擦戏数
friction.mult(normal); // 乘以正向力
) {
movers[i].applyForce(friction);
}
movers[i].applyForce(wind);
movers[i].applyForce(gravity);
movers[i].update();
movers[i].display();
movers[i].checkEdges();
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
println(mag());
}
}
}
class Mover {
PVector location;
PVector velocity;
PVector acceleration;
float mass;
color c;
Mover(float m,float x,float y) {
location = new PVector(x,y);
velocity = ,);
acceleration = ,);
mass = m;
c = color(random(),random(),random());
}
void applyForce(PVector force) {
PVector newVector = force.get();
newVector.div(mass);
acceleration.add(newVector);
}
void update() {
velocity.add(acceleration);
location.add(velocity);
acceleration.mult();
}
void display() {
stroke();
strokeWeight();
fill(c);
//fill(random(255),random(255),random(255));
ellipse(location.x,location.y,mass * ,mass * );
}
void checkEdges() {
if(location.x > width) {
location.x = width;
velocity.x *= -;
} ) {
velocity.x *= -;
location.x = ;
}
if(location.y > height) {
velocity.y *= -;
location.y = height;
}
}
}
2.8 空气和流体阻力
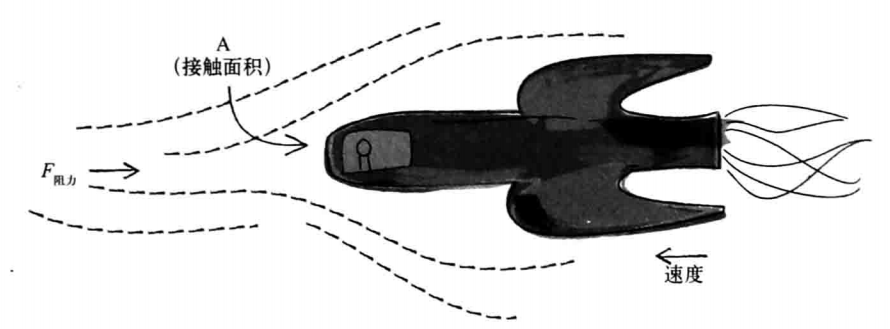
[阻力公式]

Fd代表阻力,我们的最终目的就是计算这个阻力向量,将它传入applyForce()函数
-1/2是一个常量:-0.5.对我们来说,这个数值并没有多少意义,因为这只是一个随意编造的常量.但有一点很重要,该常量必须是一个负数,这代表阻力的方向和速度的方向相反(和摩擦力类似)
ρ是希腊字母rho,它代表流体的密度,在这里我们并不需要关心它.为了简化问题,我们假设流体的密度是1.
v代表物体的移动速率.前面我们已经接触过它了,速率等于速度向量的大小:velocity.magnitude(),v2指v的平方或者v*v
A代表物体前端推动流体(或气体)流动部分的面积.举个例子,根据空气动力学设计的兰博基尼跑车所受的空气阻力肯定比四四方方的沃尔沃汽车小.为了方便模拟,我们假定物体都是球形的,因此,这个变量也将被我们忽略
Cd是阻力系数,它和摩擦系数ρ类似,是一个常量.我们可以根据阻力的强弱确定它的大小
v看起来是否很熟悉?它代表速度的单位向量,也就是velocity.normalize().和摩擦力一样,阻力的方向也和物体的运动方向相反
[简化版的阻力公式]
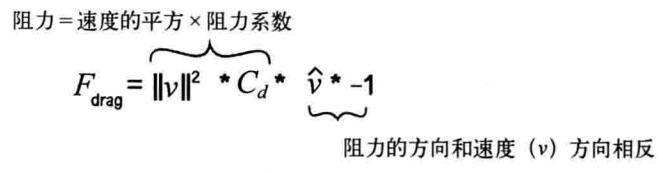
float c = 0.1; // 阻力系数 float speed = v.mag(); // 速度 float dragMagnitude = c * speed * speed; // 公式的第一部分(大小) PVector drag = velocity.get(); drag.mult(-); // 公式的第二部分(方向) drag.normalize(); drag.mult(dragMagnitude); // 合并大小和方向
// 流体阻力公式的实现
void drag(Liquid l) {
float speed = velocity.mag();
float dragMagnitude = l.c * speed * speed; // 力的大小
PVector drag = velocity.get();
drag.mult(-);
drag.normalize(); // 力的方向:与速度相反
drag.mult(dragMagnitude); // 最终确定力:大小和方向
applyForce(drag); // 应用力
}

Mover[] movers = ];
Liquid liquid;
void setup() {
size(,);
reset();
liquid = ,height / ,width, height / ,0.1);
}
void draw() {
background();
liquid.display();
; i < movers.length; i++) {
if(liquid.contains(movers[i])) {
PVector dragForce = liquid.drag(movers[i]);
movers[i].applyForce(dragForce);
}
PVector gravity = ,0.1 * movers[i].mass);
movers[i].applyForce(gravity);
movers[i].update();
movers[i].display();
movers[i].checkEdges();
}
fill();
text(,);
}
void mousePressed() {
reset();
}
void reset() {
; i < movers.length; i++) {
movers[i] = ), + i * ,);
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
println(mag());
}
}
}
class Mover {
PVector location;
PVector velocity;
PVector acceleration;
float mass;
color c;
Mover(float m,float x,float y) {
location = new PVector(x,y);
velocity = ,);
acceleration = ,);
mass = m;
c = color(random(),random(),random());
}
void applyForce(PVector force) {
PVector newVector = force.get();
newVector.div(mass);
acceleration.add(newVector);
}
void update() {
velocity.add(acceleration);
location.add(velocity);
acceleration.mult();
}
void display() {
stroke();
strokeWeight();
fill(c);
//fill(random(255),random(255),random(255));
ellipse(location.x,location.y,mass * ,mass * );
}
void checkEdges() {
if(location.y > height) {
velocity.y *= -0.9; // a little dampening when hitting the bottom
location.y = height;
}
}
}
class Liquid {
float x,y,w,h;
// 摩擦戏数
float c;
Liquid(float x_,float y_,float w_,float h_,float c_) {
x = x_;
y = y_;
w = w_;
h = h_;
c = c_;
}
// is the mover in the liquid?
boolean contains(Mover m) {
PVector l = m.location;
if(l.x > x && l.x < x + w && l.y > y && l.y < y + h) {
return true;
} else {
return false;
}
}
PVector drag(Mover m) {
float speed = m.velocity.mag();
float dragMagnitude = c * speed * speed;
PVector dragForce = m.velocity.get();
dragForce.mult(-);
dragForce.normalize();
dragForce.mult(dragMagnitude);
return dragForce;
}
void display() {
noStroke();
fill();
rect(x,y,w,h);
}
}
2.9 引力
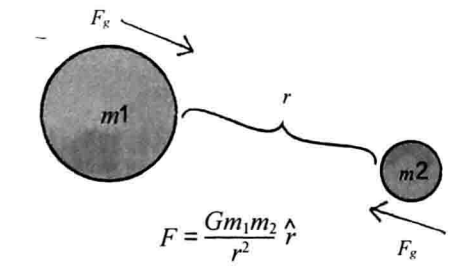
[引力公式]
F代表引力,我们最终的目的就是计算这个引力向量,将它传入applyForce()函数
G是万有引力常量,在地球上,它的值等于6.674 28 x 10-11N*m2/kg2.对物理学家来说,这个值非常重要,但在Processing编程中,它并不重要.对我们而言,它只是一个常量,用于控制引力的强弱.我们可以随意地将它假定为1,不用考虑这个值是否正确.
m1和m2代表两个物体的质量.在前面牛顿第二定律(F = M * A)的模拟中,我们忽略了质量,因为显示在屏幕上的圆并没有真正的质量.但我们也可以加入质量的作用,让质量更大的物体产生更大的引力,这样一来,整个模拟过程将变得更加有趣
r代表由物体1指向物体2的单位向量.为了得到整个方向向量,我们将两个物体的位置方向相减
r2表示物体距离的平方.公式的分子包含G,m1和m2,分子越大,分数值越大,因此G,m1和m2的值越大,引力也越大;分母越大,分数值越小,因此引力的强弱和距离的平方成反比.物体距离越远,引力越弱;物体距离越近,引力越强.
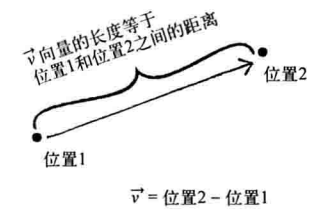
PVector force = PVector.sub(location1,location2); // 由一个对象指向另一个对象的向量,location2指向location1 float distance = force.magnitude(); // 向量的长度(大小)等于对象之间的距离 float m = (G * mass1 * mss2) / (distance * distance); // 用重力公式计算力的大小 force.normalize(); // 单位化力向量 force.mult(m); // 设置力的大小

Mover m;
Attractor a;
void setup() {
size(,);
m = new Mover();
a = new Attractor();
}
void draw() {
//background(255);
PVector force = a.attract(m);
m.applyForce(force);
m.update();
a.drag();
a.hover(mouseX,mouseY);
a.display();
m.display();
}
void mousePressed() {
a.clicked(mouseX,mouseY);
}
void mouseReleased() {
a.stopDragging();
}
class Attractor {
float mass;
float G;
PVector location;
boolean dragging = false;
boolean rollover = false;
PVector dragOffset;
Attractor() {
location = ,height / );
mass = ;
G = ;
dragOffset = new PVector(0.0,0.0);
}
PVector attract(Mover m) {
PVector force = location.get();
force.sub(m.location);
float distance = force.mag();
distance = constrain(distance,5.0,25.0);
force.normalize();
float strength = (G * mass * m.mass) / (distance * distance);
force.mult(strength);
return force;
}
void display() {
ellipseMode(CENTER);
stroke();
strokeWeight();
if(dragging) {
fill();
} else if(rollover) {
fill();
} else {
fill(,);
}
ellipse(location.x,location.y,mass * ,mass *);
}
void clicked(int mx,int my) {
float d = dist(mx,my,location.x,location.y);
if(d < mass) {
dragging = true;
dragOffset.x = location.x - mx;
dragOffset.y = location.y - my;
}
}
void hover(int mx,int my) {
float d = dist(mx,my,location.x,location.y);
if(d < mass) {
rollover = true;
} else {
rollover = false;
}
}
void stopDragging() {
dragging = false;
}
void drag() {
if(dragging) {
location.x = mouseX + dragOffset.x;
location.y = mouseY + dragOffset.y;
}
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
println(mag());
}
}
}
class Mover {
PVector location;
PVector velocity;
PVector acceleration;
float mass;
color c;
Mover() {
location = ,);
velocity = ,);
acceleration = ,);
mass = ;
c = color(random(),random(),random());
}
void applyForce(PVector force) {
PVector newVector = force.get();
newVector.div(mass);
acceleration.add(newVector);
}
void update() {
velocity.add(acceleration);
location.add(velocity);
acceleration.mult();
}
void display() {
stroke();
strokeWeight();
fill(c);
//fill(random(255),random(255),random(255));
ellipse(location.x,location.y,mass * ,mass * );
}
void checkEdges() {
if(location.x > width) {
location.x = ;
} ) {
location.x = width;
}
if(location.y > height) {
velocity.y *= -;
location.y = height;
}
}
}
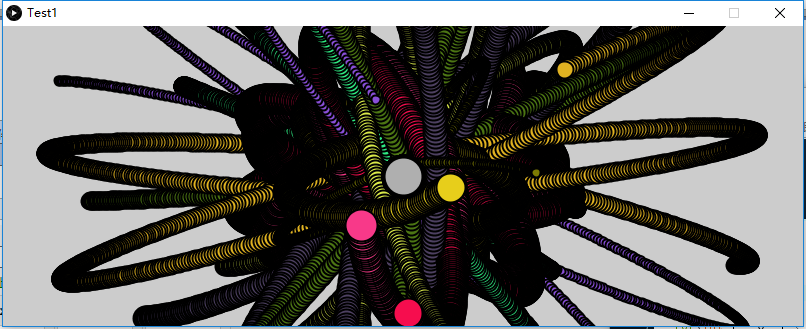
Mover[] movers = ];
Attractor a;
void setup() {
size(,);
; i < movers.length; i++) {
movers[i] = ),random(width),random(height));
}
a = new Attractor();
}
void draw() {
//background(255);
a.display();
a.drag();
a.hover(mouseX,mouseY);
; i < movers.length; i++) {
PVector force = a.attract(movers[i]);
movers[i].applyForce(force);
movers[i].update();
movers[i].display();
}
}
void mousePressed() {
a.clicked(mouseX,mouseY);
}
void mouseReleased() {
a.stopDragging();
}
class Attractor {
float mass;
float G;
PVector location;
boolean dragging = false;
boolean rollover = false;
PVector dragOffset;
Attractor() {
location = ,height / );
mass = ;
G = ;
dragOffset = new PVector(0.0,0.0);
}
PVector attract(Mover m) {
PVector force = location.get();
force.sub(m.location);
float distance = force.mag();
distance = constrain(distance,5.0,25.0);
force.normalize();
float strength = (G * mass * m.mass) / (distance * distance);
force.mult(strength);
return force;
}
void display() {
ellipseMode(CENTER);
stroke();
strokeWeight();
if(dragging) {
fill();
} else if(rollover) {
fill();
} else {
fill(,);
}
ellipse(location.x,location.y,mass * ,mass *);
}
void clicked(int mx,int my) {
float d = dist(mx,my,location.x,location.y);
if(d < mass) {
dragging = true;
dragOffset.x = location.x - mx;
dragOffset.y = location.y - my;
}
}
void hover(int mx,int my) {
float d = dist(mx,my,location.x,location.y);
if(d < mass) {
rollover = true;
} else {
rollover = false;
}
}
void stopDragging() {
dragging = false;
}
void drag() {
if(dragging) {
location.x = mouseX + dragOffset.x;
location.y = mouseY + dragOffset.y;
}
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
println(mag());
}
}
}
class Mover {
PVector location;
PVector velocity;
PVector acceleration;
float mass;
color c;
Mover(float m,float x,float y) {
mass = m;
location = new PVector(random(width),random(height));
velocity = ,);
acceleration = ,);
c = color(random(),random(),random());
}
void applyForce(PVector force) {
PVector newVector = force.get();
newVector.div(mass);
acceleration.add(newVector);
}
void update() {
velocity.add(acceleration);
location.add(velocity);
acceleration.mult();
}
void display() {
stroke();
strokeWeight();
fill(c);
//fill(random(255),random(255),random(255));
ellipse(location.x,location.y,mass * ,mass * );
}
void checkEdges() {
if(location.x > width) {
location.x = ;
} ) {
location.x = width;
}
if(location.y > height) {
velocity.y *= -;
location.y = height;
}
}
}
2.10 万有引(斥)力

Mover[] movers = ];
void setup() {
size(,);
; i < movers.length; i++) {
movers[i] = ),random(width),random(height));
}
}
void draw() {
background();
; i < movers.length; i++) {
; j < movers.length; j++) {
if(i != j) {
PVector force = movers[j].attract(movers[i]);
movers[i].applyForce(force);
}
}
movers[i].update();
movers[i].display();
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
println(mag());
}
}
}
class Mover {
PVector location;
PVector velocity;
PVector acceleration;
float mass;
float G;
color c;
Mover(float m,float x,float y) {
mass = m;
location = new PVector(random(width),random(height));
velocity = ,);
acceleration = ,);
G = ;
c = color(random(),random(),random());
}
void applyForce(PVector force) {
PVector newVector = force.get();
newVector.div(mass);
acceleration.add(newVector);
}
void update() {
velocity.add(acceleration);
location.add(velocity);
acceleration.mult();
}
void display() {
stroke();
strokeWeight();
fill(c);
//fill(random(255),random(255),random(255));
ellipse(location.x,location.y,mass * ,mass * );
}
PVector attract(Mover m) {
PVector force = location.get();
force.sub(m.location);
float distance = force.mag();
distance = constrain(distance,5.0,25.0);
force.normalize();
float strength = (G * mass * m.mass) / (distance * distance);
force.mult(strength);
return force;
}
}
第3章 震荡
3.1 角度
弧度也是角的度量单位,它是角所对的弧长除以半径后得到的值
3.2 角运动
位置 = 位置 + 速度 角度 = 角度 + 角速度
速度 = 速度 + 加速度 速度 = 速度 + 加速度

;
;
float aAcceleration = 0.001;
void setup() {
size(,);
}
void draw() {
background();
fill();
stroke();
rectMode(CENTER);
translate(width / ,height / );
rotate(angle);
line(-,,,);
ellipse(,,,);
ellipse(-,,,);
aVelocity += aAcceleration;
angle += aVelocity;
}
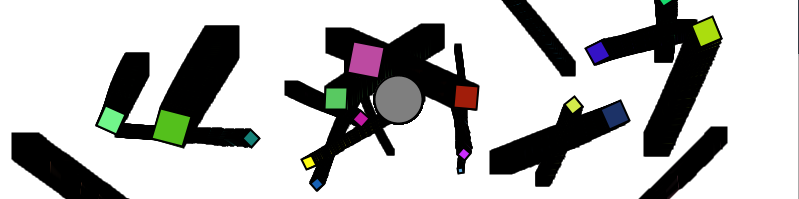
Mover[] movers = ];
Attractor a;
void setup() {
size(,);
background();
; i < movers.length; i++) {
movers[i] = ),random(width),random(height));
}
a = new Attractor();
}
void draw() {
//background(255);
a.display();
; i < movers.length; i++) {
PVector force = a.attract(movers[i]);
movers[i].applyForce(force);
movers[i].update();
movers[i].display();
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
println(mag());
}
}
}
class Attractor {
PVector location;
float mass;
float g;
Attractor() {
location = ,height / );
mass = ;
g = 0.4;
}
PVector attract(Mover m) {
PVector force = location.get();
force.sub(m.location);
float distance = force.mag();
distance = constrain(distance,5.0,25.0);
force.normalize();
float strength = (g * mass / mass) / (distance * distance);
force.mult(strength);
return force;
}
void display() {
stroke();
strokeWeight();
fill();
ellipse(location.x,location.y,,);
}
}
class Mover {
PVector location;
PVector velocity;
PVector acceleration;
float mass;
color c;
;
;
;
Mover(float m,float x,float y) {
mass = m;
location = new PVector(x,y);
velocity = ,),random(-,));
acceleration = ,);
c = color(random(),random(),random());
}
void applyForce(PVector force) {
PVector newVector = force.get();
newVector.div(mass);
acceleration.add(newVector);
}
void update() {
velocity.add(acceleration);
location.add(velocity);
aAcceleration = acceleration.x / 10.0;
aVelocity += aAcceleration;
aVelocity = constrain(aVelocity,-0.1,0.1);
angle += aVelocity;
acceleration.mult();
}
void display() {
stroke();
fill(c);
rectMode(CENTER);
pushMatrix();
translate(location.x,location.y);
rotate(angle);
rect(,,mass * ,mass * );
popMatrix();
}
}
3.3 三角函数
3.4 指向运动的方向
atan
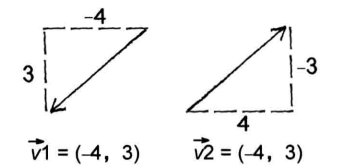
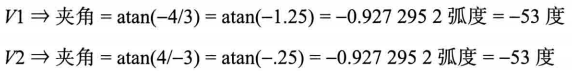
atan2 没有这个问题

Mover mover;
void setup() {
size(,);
mover = new Mover();
}
void draw() {
//background(255);
mover.update();
mover.checkEdges();
mover.display();
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
}
class Mover {
PVector location;
PVector velocity;
PVector acceleration;
float topspeed;
float xoff,yoff;
;
Mover() {
location = ,height / );
velocity = ,);
topspeed = ;
xoff = ;
yoff = ;
}
void update() {
PVector mouse = new PVector(mouseX,mouseY);
PVector dir = mouse.get();
dir.sub(location);
dir.normalize();
dir.mult(0.5);
acceleration = dir;
velocity.add(acceleration);
velocity.limit(topspeed);
location.add(velocity);
}
void display() {
float theta = velocity.heading2D();
stroke();
strokeWeight();
fill();
pushMatrix();
rectMode(CENTER);
translate(location.x,location.y);
rotate(theta);
rect(,,,);
popMatrix();
}
void checkEdges() {
if(location.x > width) {
location.x = ;
} ) {
location.x = width;
}
if(location.y > height) {
location.y = ;
} ) {
location.y = height;
}
}
}
3.5 极坐标系和笛卡儿坐标系

;
;
void setup() {
size(,);
background();
smooth();
}
void draw() {
float x = r * cos(theta);
float y = r * sin(theta);
noStroke();
fill();
ellipse(x + width / ,y + height / ,,);
r += 0.03;
theta += 0.01;
}
3.6 振荡振幅和和周期
简谐运动
物体按正弦(余弦)曲线周期性振荡.
简谐运动可以表示为位置和时间的函数,它有以下两个参数:
振幅 离开运动中心的最大就距离
周期 完成一次往复运动所花费的时间
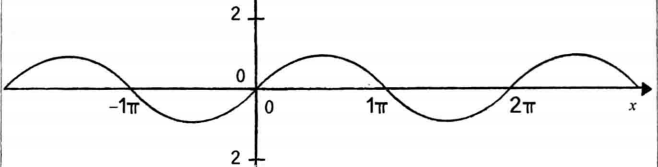
曲线的振幅是1,周期是2π.正弦函数的结果从来不会大于1,也不会小于-1.每隔2π弧度波形就会重复
本书中,Processing的时间单位是帧数
void setup() {
size(,);
}
void draw() {
// background(255);
; // 周期
; ..
float x = amplitude * cos(TWO_PI * frameCount / period);
stroke();
fill();
translate(width / ,height / );
line(,,x,);
ellipse(x,,,);
}
3.7 带有角速度的振荡
一个以弧度为单位的圆(一个圆周为2π,即:360度=2π),在单位时间内所走的弧度即为角速度.公式为:ω=Ч/t(Ч为所走过弧度,t为时间)ω的单位为:弧度每秒
;
float aVelocity = 0.05;;
void setup() {
size(,);
}
void draw() {
background();
;
float x = amplitude * cos(angle);
angle += aVelocity;
ellipseMode(CENTER);
stroke();
fill();
translate(width / ,height / );
line(,,x,);
ellipse(x,,,);
}

Oscillator[] oscillators = ];
void setup() {
size(,);
background();
; i < oscillators.length; i++) {
oscillators[i] = new Oscillator();
}
}
void draw() {
background();
; i < oscillators.length; i++) {
oscillators[i].oscillate();
oscillators[i].display();
}
}
class Oscillator {
PVector angle;
PVector velocity;
PVector amplitude;
color c;
Oscillator() {
angle = new PVector();
velocity = new PVector(random(-0.05,0.05),random(-0.05,0.05));
amplitude = ),random(height / ));
c = color(random(),random(),random());
}
void oscillate() {
angle.add(velocity);
}
void display() {
float x = sin(angle.x) * amplitude.x;
float y = sin(angle.y) * amplitude.y;
pushMatrix();
translate(width / ,height / );
stroke();
fill(c);
line(,,x,y);
ellipse(x,y,,);
popMatrix();
}
}
class PVector {
float x;
float y;
PVector() {
x = ;
y = ;
}
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
}
3.8 波
size(,);
;
float angleVel = 0.2;
;
; x <= width; x += ) {
float y = amplitude * sin(angle);
ellipse(x,y + height / ,,);
angle += angleVel;
}
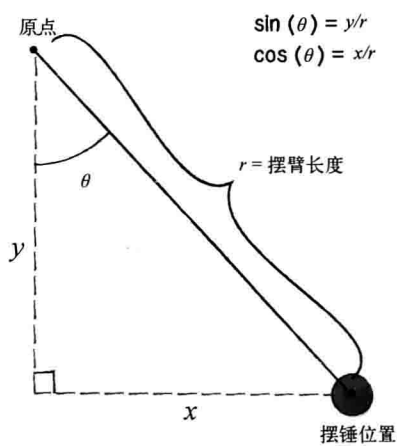
3.9 三角函数和力:钟摆

Pendulum p;
void setup() {
size(,);
p = ,),);
}
void draw() {
//background(255);
p.go();
}
class Pendulum {
PVector location; // 摆锤位置
PVector origin; // 枢轴点位置
float r; // 摆臂长度
float angle; // 摆臂角度
float aVelocity; // 角速度
float aAcceleration; // 角加速度
float damping; // 减震幅度
Pendulum(PVector origin_,float r_) {
origin = origin_.get();
location = new PVector();
r = r_;
angle = PI / ;
aVelocity = 0.0;
aAcceleration = 0.0;
damping = 0.995;
}
void go() {
update();
display();
}
void update() {
float gravity = 0.4;
aAcceleration = (- * gravity / r) * sin(angle); // 角加速度公式
aVelocity += aAcceleration; // 标准角运动算法
angle += aVelocity;
aVelocity *= damping;
}
void display() {
location = new PVector(r * sin(angle),r * cos(angle));
location.add(origin);
stroke();
line(origin.x,origin.y,location.x,location.y);
fill();
ellipse(location.x,location.y,,);
}
}
class PVector {
float x;
float y;
PVector() {
x = ;
y = ;
}
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
}
3.10 弹力
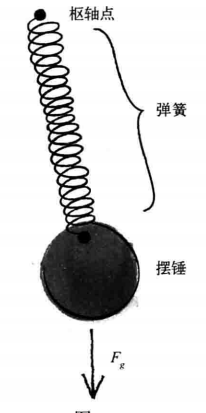
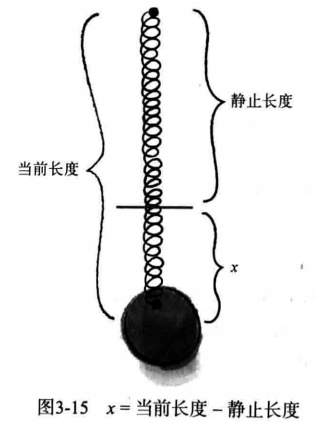


Fspring = -k * x
k是一个常量,它会影响弹力的大小.
x代表弹簧的形变,也就是当前长度和静止长度的差.静止长度被定义为弹簧在平衡状态下的长度

Bob bob;
Spring spring;
void setup() {
size(,);
spring = ,,);
bob = ,);
}
void draw() {
background();
PVector gravity = ,);
bob.applyForce(gravity);
spring.connect(bob);
spring.display();
spring.displayLine(bob);
bob.update();
bob.display();
}
class Spring {
PVector anchor;
float len;
float k = 0.1;
Spring(float x,float y,int l) {
anchor = new PVector(x,y);
len = l;
}
void connect(Bob b) {
PVector force = b.location.get();
force.sub(anchor);
float d = force.mag();
float stretch = d - len;
force.normalize();
force.mult(- * k * stretch);
b.applyForce(force);
}
void display() {
stroke();
fill();
strokeWeight();
rectMode(CENTER);
rect(anchor.x, anchor.y, , );
}
void displayLine(Bob b) {
strokeWeight();
stroke();
line(b.location.x, b.location.y, anchor.x, anchor.y);
}
}
class Bob {
PVector location;
PVector velocity;
PVector acceleration;
;
float damping = 0.98;
Bob(float x, float y) {
location = new PVector(x,y);
velocity = ,);
acceleration = ,);
}
void update() {
velocity.add(acceleration);
velocity.mult(damping);
location.add(velocity);
acceleration.mult();
}
void applyForce(PVector force) {
PVector f = force.get();
f.div(mass);
acceleration.add(f);
}
void display() {
stroke();
strokeWeight();
fill();
ellipse(location.x,location.y,mass * ,mass * );
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
}
第4章 粒子系统
1982年,卢卡斯影业的研究员William.T.Reeves正致力于电影<<星际迷航2:可汗之怒>>的制作.整部电影都围绕创始武器展开,它是一种鱼雷,能让荒芜死寂的星球发生物质重组,最后创造出适合人类居住的环境.电影中有这样一幕,某个星球在被"改造"的过程中,表面蔓延着一道火墙.粒子系统这个术语,就是在这个特效的制造过程中出现的,后来它成为计算机图形学中最常用的技术之一
"粒子系统是由许多粒子组成的用于代表模糊对象的集合.在一段特定时间内,粒子在系统中生成,移动,转化,最后消亡".
William Reeves,"Particle Systems -- A Technique for Modeling a Class of Fuzzy Objects",ACM Transactions on Graphics 2:2 (1983年4月),92
4.1 为什么需要粒子系统
4.2 单个粒子

Particle p;
void setup() {
size(,);
p = ,));
}
void draw() {
background();
p.run();
if(p.isDead()) {
println("Particle dead!");
}
}
class Particle {
PVector location;
PVector velocity;
PVector acceleration;
float lifespan;
Particle(PVector l) {
location = l.get();
acceleration = new PVector();
velocity = new PVector();
lifespan = ;
}
void run() {
update();
display();
}
void update() {
velocity.add(acceleration);
location.add(velocity);
lifespan -= 2.0;
}
void display() {
stroke(,lifespan);
fill(,lifespan);
ellipse(location.x,location.y,,);
}
boolean isDead() {
if(lifespan < 0.0) {
return true;
} else {
return false;
}
}
}
class PVector {
float x;
float y;
PVector() {
x = ;
y = ;
}
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
}
4.3 使用ArrayList
import java.util.Iterator;
ArrayList<Particle> particles;
void setup() {
size(,);
particles = new ArrayList<Particle>();
}
void draw() {
background();
particles.add(,)));
Iterator<Particle> it = particles.iterator();
while(it.hasNext()) {
Particle p = it.next();
p.run();
if(p.isDead()) {
it.remove();
}
}
}
class Particle {
PVector location;
PVector velocity;
PVector acceleration;
float lifespan;
Particle(PVector l) {
location = l.get();
acceleration = new PVector();
velocity = new PVector();
lifespan = ;
}
void run() {
update();
display();
}
void update() {
velocity.add(acceleration);
location.add(velocity);
lifespan -= 2.0;
}
void display() {
stroke(,lifespan);
fill(,lifespan);
ellipse(location.x,location.y,,);
}
boolean isDead() {
if(lifespan < 0.0) {
return true;
} else {
return false;
}
}
}
class PVector {
float x;
float y;
PVector() {
x = ;
y = ;
}
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
}
4.4 粒子系统
import java.util.Iterator;
ParticleSystem ps;
void setup() {
size(,);
ps = ,));
}
void draw() {
background();
ps.addParticle();
ps.run();
}
class ParticleSystem {
ArrayList<Particle> particles;
PVector origin;
ParticleSystem(PVector location) {
origin = location.get();
particles = new ArrayList<Particle>();
}
void addParticle() {
particles.add(new Particle(origin));
}
void run() {
Iterator<Particle> it = particles.iterator();
println(it.hasNext());
while(it.hasNext()) {
Particle p = it.next();
p.run();
if(p.isDead()) {
it.remove();
}
}
}
}
class Particle {
PVector location;
PVector velocity;
PVector acceleration;
float lifespan;
Particle(PVector l) {
location = l.get();
acceleration = new PVector();
velocity = new PVector();
lifespan = ;
}
void run() {
update();
display();
}
void update() {
velocity.add(acceleration);
location.add(velocity);
lifespan -= 2.0;
}
void display() {
stroke(,lifespan);
fill(,lifespan);
ellipse(location.x,location.y,,);
}
boolean isDead() {
if(lifespan < 0.0) {
return true;
} else {
return false;
}
}
}
class PVector {
float x;
float y;
PVector() {
x = ;
y = ;
}
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
}
4.5 由系统组成的系统
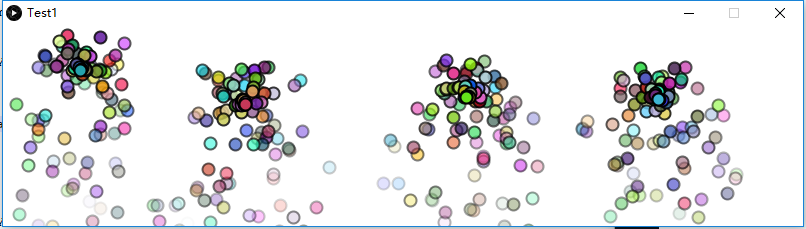
import java.util.Iterator;
ArrayList<ParticleSystem> systems;
void setup() {
size(,);
systems = new ArrayList<ParticleSystem>();
}
void draw() {
background();
for(ParticleSystem ps : systems) {
ps.run();
ps.addParticle();
}
}
void mousePressed() {
systems.add(,new PVector(mouseX,mouseY)));
}
class ParticleSystem {
ArrayList<Particle> particles;
PVector origin;
ParticleSystem(int num,PVector v) {
particles = new ArrayList<Particle>();
origin = v.get();
; i < num; i++) {
particles.add(new Particle(origin));
}
}
void addParticle() {
particles.add(new Particle(origin));
}
void addParticle(Particle p) {
particles.add(p);
}
void run() {
Iterator<Particle> it = particles.iterator();
while(it.hasNext()) {
Particle p = it.next();
p.run();
if(p.isDead()) {
it.remove();
}
}
}
boolean dead() {
if(particles.isEmpty()) {
return true;
} else {
return false;
}
}
}
class Particle {
PVector location;
PVector velocity;
PVector acceleration;
float lifespan;
color c;
Particle(PVector l) {
acceleration = ,0.05);
velocity = ,),random(-,));
location = l.get();
lifespan = ;
c = color(random(),random(),random());
}
void run() {
update();
display();
}
void update() {
velocity.add(acceleration);
location.add(velocity);
lifespan -= 2.0;
}
void display() {
stroke(,lifespan);
strokeWeight();
fill(c,lifespan);
ellipse(location.x,location.y,,);
}
boolean isDead() {
if(lifespan < 0.0) {
return true;
} else {
return false;
}
}
}
class PVector {
float x;
float y;
PVector() {
x = ;
y = ;
}
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
}
4.6 继承和多态的简介
4.7 继承基础
4.8 用继承实现粒子类
4.9 多态基础
4.10 用多态实现粒子系统
4.11 受力作用的粒子系统

import java.util.Iterator;
ParticleSystem ps;
void setup() {
size(,);
ps = ,));
}
void draw() {
background();
ps.addParticle();
ps.run();
}
class ParticleSystem {
ArrayList<Particle> particles;
PVector origin;
ParticleSystem(PVector location) {
origin = location.get();
particles = new ArrayList<Particle>();
}
void addParticle() {
);
if(r < 0.5) {
particles.add(new Particle(origin));
} else {
particles.add(new Confetti(origin));
}
}
void run() {
Iterator<Particle> it = particles.iterator();
while(it.hasNext()) {
Particle p = it.next();
p.run();
if(p.isDead()) {
it.remove();
}
}
}
}
class Particle {
PVector location;
PVector velocity;
PVector acceleration;
float lifespan;
Particle(PVector l) {
acceleration = ,0.05);
velocity = ,),random(-,));
location = l.get();
lifespan = 255.0;
}
void run() {
update();
display();
}
void update() {
velocity.add(acceleration);
location.add(velocity);
lifespan -= 2.0;
}
void display() {
stroke(,lifespan);
strokeWeight();
fill(,lifespan);
ellipse(location.x,location.y,,);
}
boolean isDead() {
if(lifespan < 0.0) {
return true;
} else {
return false;
}
}
}
class Confetti extends Particle {
Confetti(PVector l) {
super(l);
}
void display() {
rectMode(CENTER);
fill(,lifespan);
stroke(,lifespan);
strokeWeight();
pushMatrix();
translate(location.x,location.y);
,width,,TWO_PI * );
rotate(theta);
rect(,,,);
popMatrix();
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
}
4.12 带排斥对象的粒子系统

import java.util.Iterator;
ParticleSystem ps;
Repeller repeller;
void setup() {
size(,);
ps = ,));
repeller = - ,height / );
}
void draw() {
background();
ps.addParticle();
PVector gravity = ,0.1);
ps.applyForce(gravity);
ps.applyRepeller(repeller);
ps.run();
repeller.display();
}
class ParticleSystem {
ArrayList<Particle> particles;
PVector origin;
ParticleSystem(PVector location) {
origin = location.get();
particles = new ArrayList<Particle>();
}
void addParticle() {
particles.add(new Particle(origin));
}
void applyForce(PVector f) {
for(Particle p : particles) {
p.applyForce(f);
}
}
void applyRepeller(Repeller r) {
for(Particle p : particles) {
PVector force = r.repel(p);
p.applyForce(force);
}
}
void run() {
Iterator<Particle> it = particles.iterator();
while(it.hasNext()) {
Particle p = it.next();
p.run();
if(p.isDead()) {
it.remove();
}
}
}
}
class Particle {
PVector location;
PVector velocity;
PVector acceleration;
float lifespan;
;
Particle(PVector l) {
acceleration = ,0.05);
velocity = ,),random(-,));
location = l.get();
lifespan = 255.0;
}
void applyForce(PVector force) {
PVector newVector = force.get();
newVector.div(mass);
acceleration.add(newVector);
}
void run() {
update();
display();
}
void update() {
velocity.add(acceleration);
location.add(velocity);
acceleration.mult();
lifespan -= 2.0;
}
void display() {
stroke(,lifespan);
strokeWeight();
fill(,lifespan);
ellipse(location.x,location.y,,);
}
boolean isDead() {
if(lifespan < 0.0) {
return true;
} else {
return false;
}
}
}
class Repeller {
;
PVector location;
;
Repeller(float x,float y) {
location = new PVector(x,y);
}
void display() {
stroke();
fill();
ellipse(location.x,location.y,,);
}
PVector repel(Particle p) {
PVector dir = location.get();
dir.sub(p.location);
float d = dir.mag();
dir.normalize();
d = constrain(d,,);
* strength / (d * d);
dir.mult(force);
return dir;
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
}
4.13 图像纹理和加法混合
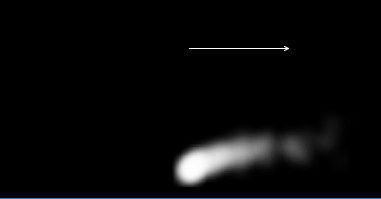
import java.util.Iterator;
import java.util.Random;
ParticleSystem ps;
Random generator;
void setup() {
size(,);
generator = new Random();
PImage img = loadImage("texture.png");
ps = ,,height-),img);
smooth();
}
void draw() {
background();
// Calculate a "wind" force based on mouse horizontal position
,width,-0.2,0.2);
PVector wind = );
ps.applyForce(wind);
ps.run();
; i < ; i++) {
ps.addParticle();
}
// Draw an arrow representing the wind force
drawVector(wind, ,),);
}
// Renders a vector object 'v' as an arrow and a location 'loc'
void drawVector(PVector v, PVector loc, float scayl) {
pushMatrix();
;
// Translate to location to render vector
translate(loc.x,loc.y);
stroke();
// Call vector heading function to get direction (note that pointing up is a heading of 0) and rotate
rotate(v.heading2D());
// Calculate length of vector & scale it to be bigger or smaller if necessary
float len = v.mag()*scayl;
// Draw three lines to make an arrow (draw pointing up since we've rotate to the proper direction)
line(,,len,);
line(len,,len-arrowsize,+arrowsize/);
line(len,,len-arrowsize,-arrowsize/);
popMatrix();
}
class ParticleSystem {
ArrayList<Particle> particles; // An arraylist for all the particles
PVector origin; // An origin point for where particles are birthed
PImage img;
ParticleSystem(int num, PVector v, PImage img_) {
particles = new ArrayList<Particle>(); // Initialize the arraylist
origin = v.get(); // Store the origin point
img = img_;
; i < num; i++) {
particles.add(new Particle(origin, img)); // Add "num" amount of particles to the arraylist
}
}
void run() {
Iterator<Particle> it = particles.iterator();
while (it.hasNext()) {
Particle p = it.next();
p.run();
if (p.dead()) {
it.remove();
}
}
}
// Method to add a force vector to all particles currently in the system
void applyForce(PVector dir) {
// Enhanced loop!!!
for (Particle p: particles) {
p.applyForce(dir);
}
}
void addParticle() {
particles.add(new Particle(origin,img));
}
void addParticle(Particle p) {
particles.add(p);
}
// A method to test if the particle system still has particles
boolean dead() {
if (particles.isEmpty()) {
return true;
} else {
return false;
}
}
}
class Particle {
PVector loc;
PVector vel;
PVector acc;
float lifespan;
PImage img;
Particle(PVector l,PImage img_) {
acc = ,);
float vx = (float) generator.nextGaussian()*0.3;
float vy = (float) generator.nextGaussian()*0.3 - 1.0;
vel = new PVector(vx,vy);
loc = l.get();
lifespan = 100.0;
img = img_;
}
void run() {
update();
render();
}
// Method to apply a force vector to the Particle object
// Note we are ignoring "mass" here
void applyForce(PVector f) {
acc.add(f);
}
// Method to update location
void update() {
vel.add(acc);
loc.add(vel);
lifespan -= 2.5;
acc.mult(); // clear Acceleration
}
// Method to display
void render() {
imageMode(CENTER);
tint(,lifespan);
image(img,loc.x,loc.y);
// Drawing a circle instead
// fill(255,lifespan);
// noStroke();
// ellipse(loc.x,loc.y,img.width,img.height);
}
// Is the particle still useful?
boolean dead() {
if (lifespan <= 0.0) {
return true;
} else {
return false;
}
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
}
第5章 物理函数库
5.1 Box2D及其适用性
5.2 获取Processing中的Box2D
5.3 Box2D基础
5.3.1 SETUP
5.3.2 DRAW
5.3.3 Box2D世界的核心元素
世界(world) 管理整个物理模拟过程,它知道坐标空间的所有信息,存放了世界中的所有物体
物体(body) Box2D世界的基础元素,有自己的位置和速度.是否感到似曾相似?在前面力和向量的模拟程序中,我们开发了很多类,Box2D的物体就等同于这些类
形状(shape) 记录所有与碰撞相关的几何信息
夹具(fixture) 将形状赋给物体,设置物体的一些属性,比如密度,摩擦系数,复原性
关节(joint) 充当两个物体之间的连接器(或者物体和世界之间的连接器)
Vec2 描述Box2D世界中的向量
http://code.google.com/p/jbox2d
5.4 生活在Box2D的世界

import shiffman.box2d.*;
import org.jbox2d.collision.shapes.*;
import org.jbox2d.common.*;
import org.jbox2d.dynamics.*;
Box2DProcessing box2d;
void setup() {
size(,);
box2d = new Box2DProcessing(this);
box2d.createWorld();
}
void draw() {
background();
Vec2 mouseWorld = box2d.coordPixelsToWorld(mouseX,mouseY);
Vec2 worldPos = ,);
Vec2 pixelPos = box2d.coordWorldToPixels(worldPos);
fill();
ellipse(pixelPos.x,pixelPos.y,,);
}
5.5 创建一个Box2D物体
5.5.1 第1步:定义一个物体
BodyDef bd = new BodyDef();
5.5.2 第2步:设置物体的定义
Vec2 center = box2d.coordPixelsToWorld(width / ,height / ); bd.postion.set(center);
物体类型:
动态(Dynamic) 大部分情况下我们会使用这个类型,一个"完全模拟"的物体.动态的物体能在Box2D的世界中运动,能和其他物体发生碰撞,并能感应环境中的力
静态(Static) 静态的物体不能发生移动(假设它的质量为无穷大).我们可以把某些固定的平台和边界当作静态物体
Kinematic 对此类物体,你可以通过设置它的速度向量来控制其移动.如果你的世界中有一个完全由用户控制的对象,你可以创建Kinematic类型的物体.注意,Kinematic的物体只会和动态的物体发生碰撞,不会和静态或者Kinematic的物体发生碰撞
bd.fixedRotation = true; // 永不旋转 bd.linearDamping = 0.8; // 线性阻尼 bd.angularDamping = 0.9; // 角速度阻尼 // 对于快速运动的物体,你必须把它的bullet属性设为true,这相当于告诉Box2D引擎:该物体的运动速度非常快,要更仔细地检查它的碰撞,防止它突然穿过其他物体 bd.bullet = true;
5.5.3 第3步:创建物体
Body body = box2d.createBody(bd);
5.5.4 第4步:为物体的初始状态设置其他属性
body.setLinearVelocity(,)); body.setAngularVelocity(1.2);
5.6 三要素:物体,形状和夹具
其实Box2D中的物体并不是直接存在于世界中,它就像脱离肉体的灵魂.对于一个有质量的物体,我们必须再定义一个形状,通过夹具将这个形状连接在物体上
Box2D中形状类的主要职责就是管理与碰撞相关的几何结构,除此之外,你还可以通过它设置一些与运动相关的属性,比如设置决定物体质量的密度属性.形状还有摩擦性和复原性("弹力").这两个属性可以通过夹具设置.
Box2D区分了物体和形状的概念,并将它们独立地放在两个对象中,这是一个很不错的设计,如此一来,用户就可以将多个形状连接到同一个物体上.
5.6.1 第1步:定义形状
PolygonShape ps = new PolygonShape(); // 将像素尺寸转换为Box2D尺寸 ); ); // 用setAsBox()函数将形状定义为矩形 ps.setAsBox(box2Dw,box2Dh);
5.6.2 第2步:创建夹具
形状和物体是两个独立的实体,为了把形状加在物体上,我们需要创建一个夹具对象
FixtureDef fd = new FixtureDef(); fd.shape = ps; fd.friction = 0.3; fd.restitution = 0.5; fd.density = 1.0;
5.6.3 第3步:用夹具将形状连接到物体上
body.createFixture(fd);
BodDef bd = new BodyDef(); 第1步:定义物体 bd.position.,height / )); Body body = box2d.createBody(bd); 第2步:创建物体 PolygonShape ps = new PolygonShape(); 第3步:定义形状 ); ); ps.setAsBox(w,h); Fixture fd = new FixtureDef(); 第4步:定义夹具 fd.shape = ps; fd.density = ; fd.friction = 0.3; fd.restitution = 0.5; body.createFixture(fd); 第5步:用夹具把形状连接到物体上
5.7 Box2D和Processing的结合
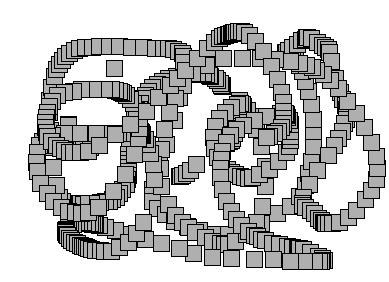
ArrayList<Box> boxes;
void setup() {
size(,);
boxes = new ArrayList<Box>();
}
void draw() {
background();
if(mousePressed) {
Box p = new Box(mouseX,mouseY);
boxes.add(p);
}
for(Box b: boxes) {
b.display();
}
}
class Box {
float x,y;
float w,h;
Box(float _x,float _y) {
x = _x;
y = _y;
w = ;
h = ;
}
void display() {
fill();
stroke();
rectMode(CENTER);
rect(x,y,w,h);
}
}
5.7.1 第1步:在主程序(即setup()和draw()函数)中添加Box2D
5.7.2 第2步:建立Processing盒子对象和Box2D物体对象之间的联系
请注意,Box2D坐标系统的转动方向和Processing坐标系统相反,因此我们需要将角度乘以-1.
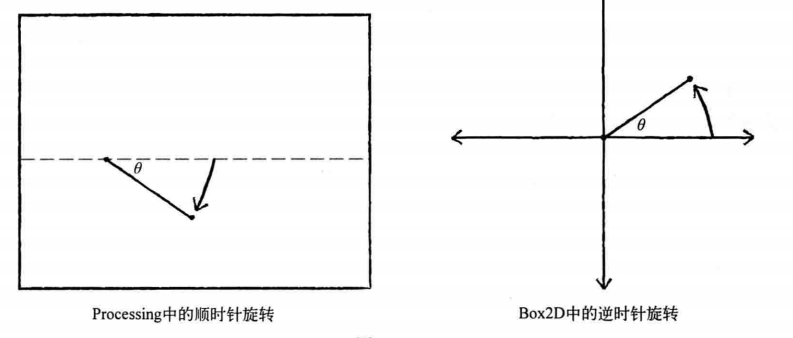

import shiffman.box2d.*;
import org.jbox2d.collision.shapes.*;
import org.jbox2d.common.*;
import org.jbox2d.dynamics.*;
ArrayList<Box> boxes;
Box2DProcessing box2d;
void setup() {
size(,);
box2d = new Box2DProcessing(this);
box2d.createWorld();
boxes = new ArrayList<Box>();
}
void draw() {
background();
box2d.step();
Box p = new Box(mouseX,mouseY);
boxes.add(p);
for(Box b: boxes) {
b.display();
}
}
class Box {
Body body;
// float x,y; 不需要(x,y)变量,因为现在物体能够管理自己的位置
// 从技术层面说,物体还可以记录自己的高度和宽度,但由于在盒子对象的生存期内,Box2D不会改变它的高度和宽度,因此我们可以继续在盒子对象中记录它们,以便于盒子的绘制
float w,h;
Box(float x,float y) {
w = ;
h = ;
BodyDef bd = new BodyDef();
bd.type = BodyType.DYNAMIC;
bd.position.set(box2d.coordPixelsToWorld(x,y));
body = box2d.createBody(bd);
PolygonShape ps = new PolygonShape();
);
);
ps.setAsBox(box2dW,box2dH);
FixtureDef fd = new FixtureDef();
fd.shape = ps;
fd.density = ;
fd.friction = 0.3;
fd.restitution = 0.5;
body.createFixture(fd);
}
void display() {
Vec2 pos = box2d.getBodyPixelCoord(body);
float a = body.getAngle();
pushMatrix();
translate(pos.x,pos.y);
rotate(-a);
fill();
stroke();
rectMode(CENTER);
rect(,,w,h);
popMatrix();
}
void killBody() {
box2d.destroyBody(body);
}
}
5.8 固定的Box2D对象

import shiffman.box2d.*;
import org.jbox2d.collision.shapes.*;
import org.jbox2d.common.*;
import org.jbox2d.dynamics.*;
Box2DProcessing box2d;
ArrayList<Box> boxes;
ArrayList<Boundary> boundaries;
void setup() {
size(,);
box2d = new Box2DProcessing(this);
box2d.createWorld();
box2d.setGravity(,-);
boxes = new ArrayList<Box>();
boundaries = new ArrayList<Boundary>();
boundaries.add(,height - ,width / - ,));
boundaries.add( * width / ,height - ,width / - ,));
}
void draw() {
background();
box2d.step();
Box p = new Box(mouseX,mouseY);
boxes.add(p);
for(Box b: boxes) {
b.display();
}
; i >= ; i--) {
Box b = boxes.get(i);
if(b.done()) {
boxes.remove(i);
}
}
}
class Boundary {
float x,y;
float w,h;
Body b;
Boundary(float x_,float y_,float w_,float h_) {
x = x_;
y = y_;
w = w_;
h = h_;
BodyDef bd = new BodyDef();
bd.position.set(box2d.coordPixelsToWorld(x,y));
bd.type = BodyType.STATIC;
b = box2d.createBody(bd);
PolygonShape ps = new PolygonShape();
);
);
ps.setAsBox(box2dW,box2dH);
b.createFixture(ps,);
}
void display() {
fill();
stroke();
rectMode(CENTER);
rect(x,y,w,h);
}
}
class Box {
Body body;
float w;
float h;
// Constructor
Box(float x, float y) {
w = random(, );
h = random(, );
// Add the box to the box2d world
makeBody(new Vec2(x, y), w, h);
}
// This function removes the particle from the box2d world
void killBody() {
box2d.destroyBody(body);
}
// Is the particle ready for deletion?
boolean done() {
// Let's find the screen position of the particle
Vec2 pos = box2d.getBodyPixelCoord(body);
// Is it off the bottom of the screen?
if (pos.y > height+w*h) {
killBody();
return true;
}
return false;
}
// Drawing the box
void display() {
// We look at each body and get its screen position
Vec2 pos = box2d.getBodyPixelCoord(body);
// Get its angle of rotation
float a = body.getAngle();
rectMode(CENTER);
pushMatrix();
translate(pos.x, pos.y);
rotate(-a);
fill();
stroke();
strokeWeight();
rect(, , w, h);
popMatrix();
}
// This function adds the rectangle to the box2d world
void makeBody(Vec2 center, float w_, float h_) {
// Define a polygon (this is what we use for a rectangle)
PolygonShape sd = new PolygonShape();
);
);
sd.setAsBox(box2dW, box2dH);
// Define a fixture
FixtureDef fd = new FixtureDef();
fd.shape = sd;
// Parameters that affect physics
fd.density = ;
fd.friction = 0.3;
fd.restitution = 0.5;
// Define the body and make it from the shape
BodyDef bd = new BodyDef();
bd.type = BodyType.DYNAMIC;
bd.position.set(box2d.coordPixelsToWorld(center));
body = box2d.createBody(bd);
body.createFixture(fd);
// Give it some initial random velocity
body.setLinearVelocity(, ), random(, )));
body.setAngularVelocity(random(-, ));
}
}
5.9 弯曲的边界
5.9.1 第1步:定义一个物体
5.9.2 第2步:定义形状
5.9.3 第3步:配置形状
5.9.4 第4步:使用夹具将形状连接到物体上
import shiffman.box2d.*;
import org.jbox2d.collision.shapes.*;
import org.jbox2d.common.*;
import org.jbox2d.dynamics.*;
import org.jbox2d.dynamics.*;
Box2DProcessing box2d;
ArrayList<Particle> particles;
Surface surface;
void setup() {
size(,);
smooth();
box2d = new Box2DProcessing(this);
box2d.createWorld();
box2d.setGravity(, -);
particles = new ArrayList<Particle>();
surface = new Surface();
}
void draw() {
) < 0.5) {
,);
particles.add(,,sz));
}
box2d.step();
background();
surface.display();
for (Particle p: particles) {
p.display();
}
; i >= ; i--) {
Particle p = particles.get(i);
if (p.done()) {
particles.remove(i);
}
}
}
class Particle {
Body body;
float r;
Particle(float x, float y, float r_) {
r = r_;
makeBody(x,y,r);
}
void killBody() {
box2d.destroyBody(body);
}
boolean done() {
Vec2 pos = box2d.getBodyPixelCoord(body);
) {
killBody();
return true;
}
return false;
}
void display() {
Vec2 pos = box2d.getBodyPixelCoord(body);
float a = body.getAngle();
pushMatrix();
translate(pos.x,pos.y);
rotate(-a);
fill();
stroke();
strokeWeight();
ellipse(,,r*,r*);
line(,,r,);
popMatrix();
}
void makeBody(float x, float y, float r) {
BodyDef bd = new BodyDef();
bd.position = box2d.coordPixelsToWorld(x,y);
bd.type = BodyType.DYNAMIC;
body = box2d.world.createBody(bd);
CircleShape cs = new CircleShape();
cs.m_radius = box2d.scalarPixelsToWorld(r);
FixtureDef fd = new FixtureDef();
fd.shape = cs;
fd.density = ;
fd.friction = 0.01;
fd.restitution = 0.3;
body.createFixture(fd);
body.setLinearVelocity(new Vec2(random(-10f,10f),random(5f,10f)));
body.setAngularVelocity(random(-,));
}
}
class Surface {
ArrayList<Vec2> surface;
Surface() {
surface = new ArrayList<Vec2>();
ChainShape chain = new ChainShape();
;
; x > -; x -= ) {
,,,height-);
theta += 0.15;
surface.add(new Vec2(x,y));
}
Vec2[] vertices = new Vec2[surface.size()];
; i < vertices.length; i++) {
Vec2 edge = box2d.coordPixelsToWorld(surface.get(i));
vertices[i] = edge;
}
chain.createChain(vertices,vertices.length);
BodyDef bd = new BodyDef();
bd.position.set(0.0f,0.0f);
Body body = box2d.createBody(bd);
body.createFixture(chain,);
}
void display() {
strokeWeight();
stroke();
noFill();
beginShape();
for (Vec2 v: surface) {
vertex(v.x,v.y);
}
endShape();
}
}
5.10 复杂的形状

import shiffman.box2d.*;
import org.jbox2d.collision.shapes.*;
import org.jbox2d.common.*;
import org.jbox2d.dynamics.*;
Box2DProcessing box2d;
ArrayList<Boundary> boundaries;
ArrayList<CustomShape> polygons;
void setup() {
size(,);
smooth();
box2d = new Box2DProcessing(this);
box2d.createWorld();
box2d.setGravity(, -);
polygons = new ArrayList<CustomShape>();
boundaries = new ArrayList<Boundary>();
boundaries.add(,height-,width/-,,));
boundaries.add(*width/,height-,width/-,,));
boundaries.add(,height/,,height,));
boundaries.add(,height/,,height,));
}
void draw() {
background();
box2d.step();
for (Boundary wall: boundaries) {
wall.display();
}
for (CustomShape cs: polygons) {
cs.display();
}
; i >= ; i--) {
CustomShape cs = polygons.get(i);
if (cs.done()) {
polygons.remove(i);
}
}
}
void mousePressed() {
CustomShape cs = new CustomShape(mouseX,mouseY);
polygons.add(cs);
}
class Boundary {
float x;
float y;
float w;
float h;
Body b;
Boundary(float x_,float y_, float w_, float h_, float a) {
x = x_;
y = y_;
w = w_;
h = h_;
PolygonShape sd = new PolygonShape();
);
);
sd.setAsBox(box2dW, box2dH);
BodyDef bd = new BodyDef();
bd.type = BodyType.STATIC;
bd.angle = a;
bd.position.set(box2d.coordPixelsToWorld(x,y));
b = box2d.createBody(bd);
b.createFixture(sd,);
}
void display() {
fill();
stroke();
strokeWeight();
rectMode(CENTER);
float a = b.getAngle();
pushMatrix();
translate(x,y);
rotate(-a);
rect(,,w,h);
popMatrix();
}
}
class CustomShape {
Body body;
CustomShape(float x, float y) {
makeBody(new Vec2(x, y));
}
void killBody() {
box2d.destroyBody(body);
}
boolean done() {
Vec2 pos = box2d.getBodyPixelCoord(body);
if (pos.y > height) {
killBody();
return true;
}
return false;
}
void display() {
Vec2 pos = box2d.getBodyPixelCoord(body);
float a = body.getAngle();
Fixture f = body.getFixtureList();
PolygonShape ps = (PolygonShape) f.getShape();
rectMode(CENTER);
pushMatrix();
translate(pos.x, pos.y);
rotate(-a);
fill();
stroke();
strokeWeight();
beginShape();
; i < ps.getVertexCount(); i++) {
Vec2 v = box2d.vectorWorldToPixels(ps.getVertex(i));
vertex(v.x, v.y);
}
endShape(CLOSE);
popMatrix();
}
void makeBody(Vec2 center) {
Vec2[] vertices = ];
vertices[] = box2d.vectorPixelsToWorld(, ));
vertices[] = box2d.vectorPixelsToWorld(, ));
vertices[] = box2d.vectorPixelsToWorld(, -));
vertices[] = box2d.vectorPixelsToWorld(, -));
PolygonShape ps = new PolygonShape();
ps.set(vertices, vertices.length);
BodyDef bd = new BodyDef();
bd.type = BodyType.DYNAMIC;
bd.position.set(box2d.coordPixelsToWorld(center));
body = box2d.createBody(bd);
body.createFixture(ps, 1.0);
body.setLinearVelocity(, ), random(, )));
body.setAngularVelocity(random(-, ));
}
}
顶点的顺序 如果从像素的角度确定这些顶点,你必须用逆时针的顺序(当这些顶点被翻译成Box2D向量时,它们会变成顺时针的顺序,因为两个坐标系的纵坐标方向是相反的
只能创建凸边形 凹边形是一种表面向内弯曲的形状.凸边形则相反
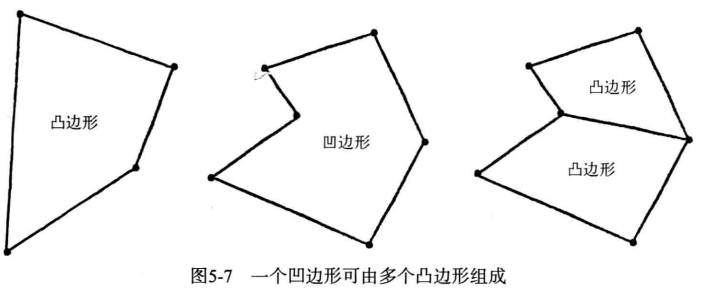

import shiffman.box2d.*;
import org.jbox2d.collision.shapes.*;
import org.jbox2d.common.*;
import org.jbox2d.dynamics.*;
Box2DProcessing box2d;
ArrayList<Boundary> boundaries;
ArrayList<Lollipop> pops;
void setup() {
size(,);
smooth();
box2d = );
box2d.createWorld();
box2d.setGravity(, -);
pops = new ArrayList<Lollipop>();
boundaries = new ArrayList<Boundary>();
boundaries.add(,height-,width/-,,));
boundaries.add(*width/,height-,width/-,,));
boundaries.add(,height/,,height,));
boundaries.add(,height/,,height,));
}
void draw() {
background();
//if (mousePressed)
box2d.step();
for (Boundary wall: boundaries) {
wall.display();
}
for (Lollipop p: pops) {
p.display();
}
; i >= ; i--) {
Lollipop p = pops.get(i);
if (p.done()) {
pops.remove(i);
}
}
}
void mousePressed() {
Lollipop p = new Lollipop(mouseX,mouseY);
pops.add(p);
}
class Lollipop {
Body body;
float w;
float h;
float r;
Lollipop(float x, float y) {
w = ;
h = ;
r = ;
makeBody(new Vec2(x, y));
}
void killBody() {
box2d.destroyBody(body);
}
boolean done() {
Vec2 pos = box2d.getBodyPixelCoord(body);
if (pos.y > height+w*h) {
killBody();
return true;
}
return false;
}
void display() {
Vec2 pos = box2d.getBodyPixelCoord(body);
float a = body.getAngle();
rectMode(CENTER);
pushMatrix();
translate(pos.x, pos.y);
rotate(-a);
fill();
stroke();
strokeWeight();
rect(,,w,h);
ellipse(, -h/, r*, r*);
popMatrix();
}
void makeBody(Vec2 center) {
BodyDef bd = new BodyDef();
bd.type = BodyType.DYNAMIC;
bd.position.set(box2d.coordPixelsToWorld(center));
body = box2d.createBody(bd);
CircleShape circle = new CircleShape();
circle.m_radius = box2d.scalarPixelsToWorld(r);
Vec2 offset = ,-h/);
offset = box2d.vectorPixelsToWorld(offset);
circle.m_p.set(offset.x,offset.y);
PolygonShape ps = new PolygonShape();
);
);
ps.setAsBox(box2dW, box2dH);
body.createFixture(ps,1.0);
body.createFixture(circle, 1.0);
body.setLinearVelocity(, ), random(, )));
body.setAngularVelocity(random(-, ));
}
}
class Boundary {
float x;
float y;
float w;
float h;
Body b;
Boundary(float x_,float y_, float w_, float h_, float a) {
x = x_;
y = y_;
w = w_;
h = h_;
PolygonShape sd = new PolygonShape();
);
);
sd.setAsBox(box2dW, box2dH);
BodyDef bd = new BodyDef();
bd.type = BodyType.STATIC;
bd.angle = a;
bd.position.set(box2d.coordPixelsToWorld(x,y));
b = box2d.createBody(bd);
b.createFixture(sd,);
}
void display() {
fill();
stroke();
strokeWeight();
rectMode(CENTER);
float a = b.getAngle();
pushMatrix();
translate(x,y);
rotate(-a);
rect(,,w,h);
popMatrix();
}
}
5.11 Box2D关节
5.11.1 步骤1:确保有两个物体
5.11.2 步骤2:定义关节
5.11.3 步骤3:配置关节的属性
5.11.4 步骤4:创建关节
5.12 回到力的话题
5.13 碰撞事件
5.13.1 步骤1:Contact对象,你能否告诉我哪两个物体发生了碰撞
5.13.2 步骤2:夹具对象,你能否告诉我你连接在哪个物体上
5.13.3 步骤3:物体,你能否告诉我你连接在哪个粒子对象上
5.14 小插曲:积分法
5.15 toxiclibs的Verlet Physics物理库
5.15.1 获取toxiclibs
5.15.2 VerletPhysics的核心元素
5.15.3 toxiclibs中的向量
5.15.4 构建toxiclibs的物理世界
5.16 toxiclibs中的粒子和弹簧
5.17 整合代码:一个简单的交互式弹簧
5.18 相连的系统I:绳子
5.19 相连的系统II:力导向图
5.20 吸引和排斥行为
第6章 自治智能体
6.1 内部的力
自治智能体指的是那些根据自身意愿做出行为决定的主体,它们不受任何领导者的影响.
自治智能体最重要的3个特性:
自治智能体对环境的感知能力是有限的
自治智能体需要处理来自外部环境的信息,并由此计算具体的行为
自治智能体没有领导者.我们并不需要太关心第三个特性
在20世界80年代,计算机科学家Craig Reynolds(http://red3d.com/cwr/)发明了一套计算有生命物体的转向(steering)行为的算法.转向行为就是:个体元素感知周围环境,用"类生命"的方式做出行为决策,包括:逃离,游走,到达,追赶和逃避等行为.
对单个自治智能体而言,这些行为并不复杂.但如果我们根据这些个体行为规则构建一个系统,也就是由众多个体组成的系统,面临的复杂性将会超出预期.最具代表性的例子就是Reynolds在"群集"行为研究中引入的"boids"模型.
6.2 车辆和转向
class Vehicle {
PVector location;
PVector velocity;
PVector acceleration;
// ...
}
Reynolds在1999年发表了论文Steering Behaviors for Autonomous Characters,他在里面用"小车"(vehicle)描述自治智能体,我们也打算用这个术语
为什么是小车?
1986年,意大利神经学家和控制论专家Valentino Braitenberg在他的著作Vehicles:Experiments in Synthetic Pyschology中用简单的内部结构描述了假想中的小车模型.Braitenberg提出的小车模型表现出了各种行为,这些行为包括恐惧,侵略,喜爱,远见和乐观.
Reynolds的灵感就来自Braitenberg.
Reynolds从动作选择,转向,驱动机构3个层面描述了理想小车模型的运动方式(由于我们不考虑小车模型的内部实现,只设想它的行为规则,因此称为理想模型)
1.动作选择 小车模型拥有一个(或多个)目的,它根据这些目的选择一个(或一系列)动作.自治智能体模型能够很好地进行这个层面模拟.
比如,小车在观察周围的环境,然后发现:"我看见一大波僵尸正在靠近,我不想让它们吃掉我的脑袋,必须想办法躲开它们".本例的目标就是"保住自己的脑袋",动作就是"躲开僵尸".Reynolds的论文描述了各种目的和相关行为,包括:寻找目标,避开障碍和跟随路径.
2.转向 一旦动作被确定,小车就开始计算下一步动作.在我们的程序中,下一步动作就是施加一个力,准确地说,这是一个转向力.Reynolds提出了转向力计算公式:转向力 = 所需速度 - 当前速度.
3.驱动机构 在大部分情况下,我们可以忽略第三个层面.在躲避僵尸的例子中,驱动力可以描述为"以最大的速度向左,向右,再向左,再向右".在Processing世界中,矩形,圆圈或三角形并没有驱动机构,因为它们都是假想出来的.但你并不能完全忽略这个层面.
为小车设计驱动效果和动画也是有实践意义的.
6.3 转向力
转向力 = 所需速度 - 当前速度
小车移动到目标位置时有一个最大速率
我们可以通过限制转向力的大小控制转向能力,这是一辆极易操控的超级赛车?还是一辆难以转动的大卡车?
转向力的限制还引入了一个关键点,让小车以最大速率移向目标位置并不是我们的最终目标,否则我们可以直接把小车的位置等于目标位置.正如Reynolds所说,最终目的是让小车用一种"贴近真实"的方式移动
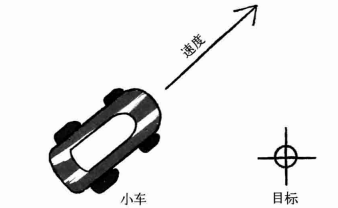

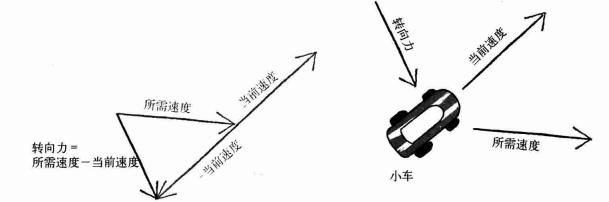


Vehicle v;
void setup() {
size(,);
v = ,height / );
}
void draw() {
//background(255);
PVector mouse = new PVector(mouseX,mouseY);
fill();
stroke();
strokeWeight();
ellipse(mouse.x,mouse.y,,);
v.seek(mouse);
v.update();
v.display();
}
class Vehicle {
PVector location;
PVector velocity;
PVector acceleration;
float r;
float maxforce; // 最大转向力
float maxspeed; // 最大速率
Vehicle(float x,float y) {
acceleration = ,);
velocity = ,-);
location = new PVector(x,y);
r = ;
maxspeed = ;
maxforce = 0.1;
}
void update() {
velocity.add(acceleration);
velocity.limit(maxspeed);
location.add(velocity);
acceleration.mult();
}
void applyForce(PVector force) {
acceleration.add(force);
}
void seek(PVector target) {
// 计算所需速度,让它的大小等于最大速率
PVector desired = target.get();
desired.sub(location);
desired.normalize();
desired.mult(maxspeed);
// Reynolds的转向力公式
PVector steer = desired.get();
steer.sub(velocity);
steer.limit(maxforce); // 限制转向力的大小
applyForce(steer);
}
void display() {
//float theta = velocity.heading2D();
;
fill();
stroke();
pushMatrix();
translate(location.x,location.y);
rotate(theta);
beginShape();
vertex(,-r * );
vertex(-r,r * );
vertex(r,r * );
endShape(CLOSE);
popMatrix();
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
}
6.4 到达行为
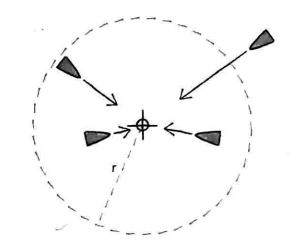
到达行为的模拟展示了"所需速度 - 当前速度"公式的神奇之处.不管引力是强是弱,它的方向总是由物体指向目标
物体的转向行为则有所不同,物体有了转向力之后,它像是在说:"我可以感知环境".转向力并非完全基于所需速度,而是同时基于所需速度和当前速度.只有那些有生命的物体才知道自己的当前速度.一个从桌子上下落的盒子并不知道它在下落,但追逐猎物的猎豹知道自己的行为
因此,转向力在本质上是当前速度的误差体现:"我应该朝着这个方向运动,实际上却朝着另一个方向运动.误差就是两个方向之间的差异".在误差的基础上施加一个转向力会创造更贴近现实的模拟效果.
在引力作用下,无论物体和目标之间的距离有多近,它所受的力永远不会远离目标;但在转向力的到达行为中,如果它朝目标运动的速度过快,转向力会让你减速以纠正误差.

Vehicle v;
void setup() {
size(,);
v = ,height / );
}
void draw() {
//background(255);
PVector mouse = new PVector(mouseX,mouseY);
fill();
stroke();
strokeWeight();
ellipse(mouse.x,mouse.y,,);
v.arrive(mouse);
v.update();
v.display();
}
class Vehicle {
PVector location;
PVector velocity;
PVector acceleration;
float r;
float maxforce; // 最大转向力
float maxspeed; // 最大速率
Vehicle(float x,float y) {
acceleration = ,);
velocity = ,-);
location = new PVector(x,y);
r = ;
maxspeed = ;
maxforce = 0.1;
}
void update() {
velocity.add(acceleration);
velocity.limit(maxspeed);
location.add(velocity);
acceleration.mult();
}
void applyForce(PVector force) {
acceleration.add(force);
}
void arrive(PVector target) {
// 计算所需速度,让它的大小等于最大速率
PVector desired = target.get();
desired.sub(location);
float d = desired.mag();
desired.normalize();
// 以物体为圆心的半径
) {
,,,maxspeed);
desired.mult(m);
} else {
desired.mult(maxspeed);
}
// Reynolds的转向力公式
PVector steer = desired.get();
steer.sub(velocity);
steer.limit(maxforce); // 限制转向力的大小
applyForce(steer);
}
void display() {
//float theta = velocity.heading2D();
;
fill();
stroke();
pushMatrix();
translate(location.x,location.y);
rotate(theta);
beginShape();
vertex(,-r * );
vertex(-r,r * );
vertex(r,r * );
endShape(CLOSE);
popMatrix();
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
}
6.5 你的意图:所需速度
游走(wandering)
"游走是一种随机性转向,它有一种远期秩序----下一帧的转向角度和当前帧的转向角度相关.这种移动方式比单纯为每一帧产生随机方向更有趣"
----Craig Reynolds(http://www.red3d.com/cwr/steer/Wander.html)

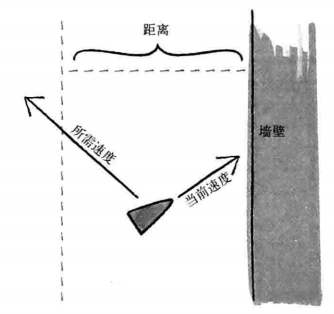
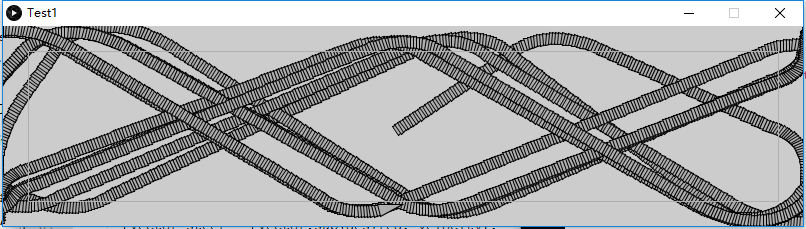
Vehicle v;
boolean debug = true;
;
void setup() {
size(,);
v = ,height / );
}
void draw() {
// background(255);
if(debug) {
stroke();
noFill();
rectMode(CENTER);
rect(width / ,height / ,width - d * ,height - d*);
}
v.boundaries();
v.run();
}
void mousePressed() {
debug = !debug;
}
class Vehicle {
PVector location;
PVector velocity;
PVector acceleration;
float r;
float maxforce; // 最大转向力
float maxspeed; // 最大速率
Vehicle(float x,float y) {
acceleration = ,);
velocity = ,-);
velocity.mult();
location = new PVector(x,y);
r = ;
maxspeed = ;
maxforce = 0.15;
}
void run() {
update();
display();
}
void update() {
velocity.add(acceleration);
velocity.limit(maxspeed);
location.add(velocity);
acceleration.mult();
}
void boundaries() {
PVector desired = null;
if(location.x < d) {
desired = new PVector(maxspeed,velocity.y);
} else if(location.x > width - d) {
desired = new PVector(-maxspeed,velocity.y);
}
if(location.y < d) {
desired = new PVector(velocity.x,maxspeed);
} else if(location.y > height - d) {
desired = new PVector(velocity.x,-maxspeed);
}
if(desired != null) {
desired.normalize();
desired.mult(maxspeed);
PVector steer = desired.get();
desired.sub(velocity);
steer.limit(maxforce);
applyForce(steer);
}
}
void applyForce(PVector force) {
acceleration.add(force);
}
void arrive(PVector target) {
// 计算所需速度,让它的大小等于最大速率
PVector desired = target.get();
desired.sub(location);
float d = desired.mag();
desired.normalize();
// 以物体为圆心的半径
) {
,,,maxspeed);
desired.mult(m);
} else {
desired.mult(maxspeed);
}
// Reynolds的转向力公式
PVector steer = desired.get();
steer.sub(velocity);
steer.limit(maxforce); // 限制转向力的大小
applyForce(steer);
}
void display() {
//float theta = velocity.heading2D();
;
fill();
stroke();
pushMatrix();
translate(location.x,location.y);
rotate(theta);
beginShape();
vertex(,-r * );
vertex(-r,r * );
vertex(r,r * );
endShape(CLOSE);
popMatrix();
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
}
6.6 流场
什么是流场?把Processing窗口当作一个网格,每个单元格都有一个向量指向特定方向,这样的模型就是流场

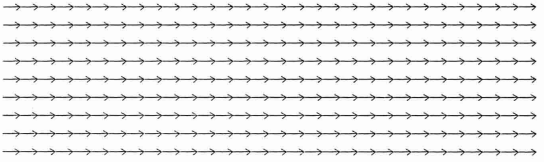


boolean debug = true;
FlowField flowfield;
ArrayList<Vehicle> vehicles;
void setup() {
size(,);
flowfield = );
vehicles = new ArrayList<Vehicle>();
; i < ; i++) {
vehicles.add(,),random(0.1,0.5)));
}
}
void draw() {
background();
if(debug) {
flowfield.display();
}
for(Vehicle v : vehicles) {
v.follow(flowfield);
v.run();
}
}
void KeyPressed() {
if (key == ' ') {
debug = !debug;
}
}
void mousePressed() {
flowfield.init();
}
class FlowField {
PVector[][] fields;
int cols,rows;
int resolution; // how large is each "cell" of the flow field
FlowField(int r) {
resolution = r;
cols = width / resolution;
rows = height / resolution;
fields = new PVector[cols][rows];
init();
}
void init() {
// Reseed noise so we get a new flow field every time
noiseSeed(());
;
; i < cols; i++) {
;
; j < rows; j++) {
,,,TWO_PI);
fields[i][j] = new PVector(cos(theta),sin(theta));
yoff += 0.1;
}
xoff += 0.1;
}
}
void drawVector(PVector v,float x,float y,float scale) {
pushMatrix();
;
translate(x,y);
stroke(,);
rotate(v.heading2D());
float len = v.mag() * scale;
line(,,len,);
popMatrix();
}
void display() {
; i < cols; i++) {
; j < rows; j++) {
drawVector(fields[i][j],i * resolution,j * resolution,resolution - );
}
}
}
PVector lookup(PVector lookup) {
,cols - ));
,rows - ));
return fields[column][row].get();
}
}
class Vehicle {
PVector location;
PVector velocity;
PVector acceleration;
float r;
float maxforce; // 最大转向力
float maxspeed; // 最大速率
Vehicle(PVector l,float ms,float mf) {
location = l.get();
r = 3.0;
maxspeed = ms;
maxforce = mf;
acceleration = ,);
velocity = ,);
}
void run() {
update();
borders();
display();
}
void follow(FlowField flow) {
PVector desired = flow.lookup(location);
desired.mult(maxspeed);
PVector steer = desired.get();
steer.sub(velocity);
steer.limit(maxforce);
applyForce(steer);
}
void applyForce(PVector force) {
acceleration.add(force);
}
void update() {
velocity.add(acceleration);
velocity.limit(maxspeed);
location.add(velocity);
acceleration.mult();
}
void display() {
);
fill();
stroke();
pushMatrix();
translate(location.x,location.y);
rotate(theta);
beginShape(TRIANGLES);
vertex(,-r * );
vertex(-r,r * );
vertex(r,r * );
endShape();
popMatrix();
}
void borders() {
if(location.x < -r) {
location.x = width + r;
}
if(location.y < -r) {
location.y = height + r;
}
if(location.x > width + r) {
location.x = -r;
}
if(location.y > height + r) {
location.y = -r;
}
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
}
6.7 点乘
public float dot(PVector v) {
return x * v.x + y * v.y + z * v.z;
}
static public float angleBetween(PVector v1,PVector v2) {
float dot = v1.dot(v2);
float theta = (float)Math.acos(dot / (v1.mag() * v2.mag()));
return theta;
}
6.8 路径跟随
定义路径的方法有很多种,一种简单的方法就是将它定义为一系列相连的点.
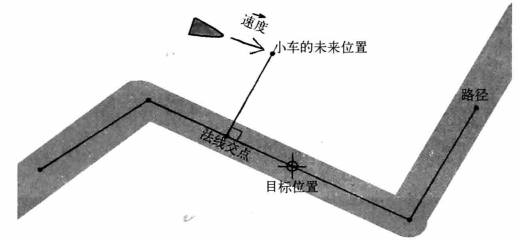
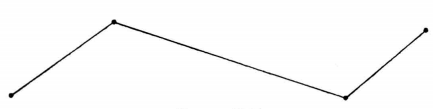
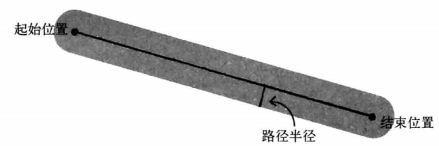

boolean debug = true;
Path path;
void setup() {
size(,);
path = new Path();
}
void draw() {
background();
path.display();
}
class Path {
PVector start;
PVector end;
float radius;
Path() {
radius = ;
start = ,height / );
end = * height / );
}
void display() {
strokeWeight(radius * );
stroke(,);
line(start.x,start.y,end.x,end.y);
strokeWeight();
stroke();
line(start.x,start.y,end.x,end.y);
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
float dot(PVector v) {
return x * v.x + y * v.y;
}
float angleBetween(PVector v2) {
float dot = this.dot(v2);
float theta = (float)Math.acos(dot / (this.mag() * v2.mag()));
return theta;
}
}
点到线的距离就等于点和线之间的法线长度.法线指的是从该点延伸并垂直于该线的向量
|A|xcos(θ)就是向量A到向量B的标量投影
Reynolds的算法指出:如果小车偏离了路径(也就是预测位置和法线交点的距离大于路径的半径),它就应该转向.

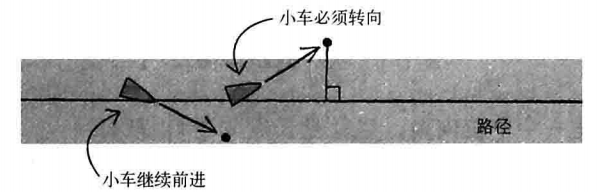
Reynolds的算法选取路径上位于法线交点前方的某个点作为目标位置
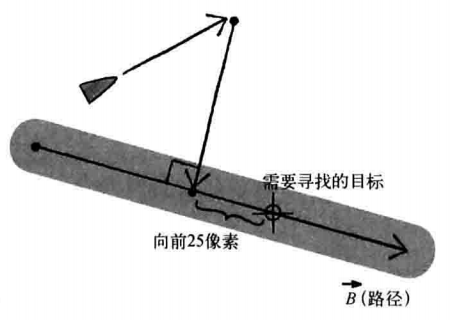

PVector getNormalPoint(PVector p,PVector a,PVector b) {
PVector ap = p.get();
ap.sub(a);
PVector ab = b.get();
ab.sub(a);
// 计算标量投影
ab.normalize();
ab.mult(ap.dot(ab));
PVector normalPoint = a.get();
normalPoint.add(ab);
return normalPoint;
}
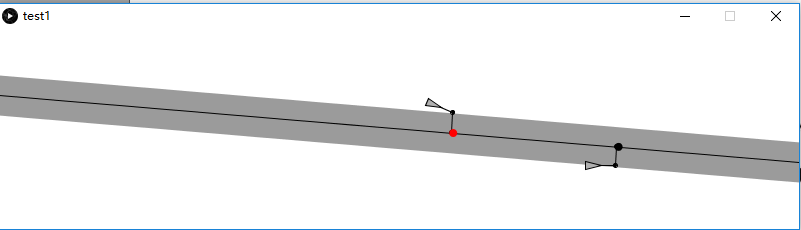
boolean debug = true;
Path path;
Vehicle car1;
Vehicle car2;
void setup() {
size(,);
path = new Path();
car1 = ,height / ),,0.05);
car2 = ,height / ),,0.1);
}
void draw() {
background();
path.display();
car1.follow(path);
car2.follow(path);
car1.run();
car2.run();
fill();
}
class Path {
PVector start;
PVector end;
float radius;
Path() {
radius = ;
start = ,height / );
end = * height / );
}
void display() {
strokeWeight(radius * );
stroke(,);
line(start.x,start.y,end.x,end.y);
strokeWeight();
stroke();
line(start.x,start.y,end.x,end.y);
}
}
class Vehicle {
PVector location;
PVector velocity;
PVector acceleration;
float r;
float maxforce;
float maxspeed;
Vehicle(PVector l,float ms,float mf) {
location = l.get();
r = 4.0;
maxspeed = ms;
maxforce = mf;
acceleration = ,);
velocity = );
}
void run() {
update();
borders();
render();
}
void follow(Path p) {
// 获取当前位置指向的任意距离的位置,现在是25
PVector predict = velocity.get();
predict.normalize();
predict.mult();
PVector predictLoc = location.get();
predictLoc.add(predict);
PVector a = p.start;
PVector b = p.end;
// 计算线上的法线点
PVector normalPoint = getNormalPoint(predictLoc,a,b);
// 获取法线点前任意一个点作为目标位置
PVector dir = b.get();
dir.sub(a);
dir.normalize();
PVector target = normalPoint.get();
target.add(dir);
//
float distance = predictLoc.dist(normalPoint);
if(distance > p.radius) {
seek(target);
}
if(debug) {
fill();
stroke();
line(location.x,location.y,predictLoc.x,predictLoc.y);
ellipse(predictLoc.x,predictLoc.y,,);
fill();
stroke();
line(predictLoc.x,predictLoc.y,normalPoint.x,normalPoint.y);
ellipse(normalPoint.x,normalPoint.y,,);
stroke();
if(distance > p.radius) {
fill(,,);
}
noStroke();
ellipse(target.x + dir.x,target.y + dir.y,,);
}
}
PVector getNormalPoint(PVector p,PVector a,PVector b) {
PVector ap = p.get();
ap.sub(a);
PVector ab = b.get();
ab.sub(a);
// 计算标量投影
ab.normalize();
ab.mult(ap.dot(ab));
PVector normalPoint = a.get();
normalPoint.add(ab);
return normalPoint;
}
void update() {
velocity.add(acceleration);
velocity.limit(maxspeed);
location.add(velocity);
acceleration.mult();
}
void applyForce(PVector force) {
acceleration.add(force);
}
void seek(PVector target) {
PVector desired = target.get();
desired.sub(location);
) {
return;
}
desired.normalize();
desired.mult(maxspeed);
PVector steer = desired.get();
desired.sub(velocity);
steer.limit(maxforce);
applyForce(steer);
}
void render() {
);
fill();
stroke();
pushMatrix();
translate(location.x,location.y);
rotate(theta);
beginShape(PConstants.TRIANGLES);
vertex(, -r * );
vertex(-r,r * );
vertex(r, r * );
endShape();
popMatrix();
}
void borders() {
if(location.x < - r) {
location.x = width + r;
}
if(location.x > width + r) {
location.x = -r;
}
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
float dot(PVector v) {
return x * v.x + y * v.y;
}
float angleBetween(PVector v2) {
float dot = this.dot(v2);
float theta = (float)Math.acos(dot / (this.mag() * v2.mag()));
return theta;
}
float dist(PVector v) {
PVector dist = this.get();
dist.sub(v);
return dist.mag();
}
}
6.9 多段路径跟随

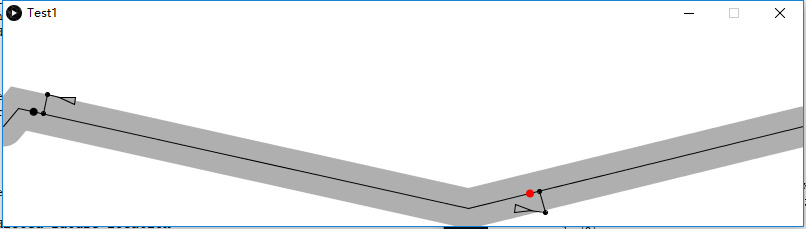
boolean debug = true;
Path path;
Vehicle car1;
Vehicle car2;
void setup() {
size(,);
newPath();
car1 = ,height / ),,0.1);
car2 = ,height / ),,0.2);
}
void draw() {
background();
path.display();
car1.follow(path);
car2.follow(path);
car1.run();
car2.run();
fill();
}
void newPath() {
path = new Path();
path.addPoint(, height / );
path.addPoint(random(, width / ),random(, height));
path.addPoint(random(width / ,width),random(, height));
path.addPoint(width, height / );
}
public void mousePressed() {
newPath();
}
class Path {
ArrayList<PVector> points;
float radius;
Path() {
radius = ;
points = new ArrayList<PVector>();
}
void addPoint(float x,float y) {
PVector point = new PVector(x,y);
points.add(point);
}
void display() {
stroke();
strokeWeight(radius * );
noFill();
beginShape();
for(PVector v : points) {
vertex(v.x,v.y);
}
endShape();
stroke();
strokeWeight();
noFill();
beginShape();
for(PVector v:points) {
vertex(v.x,v.y);
}
endShape();
}
}
class Vehicle {
PVector location;
PVector velocity;
PVector acceleration;
float r;
float maxforce;
float maxspeed;
Vehicle(PVector l,float ms,float mf) {
location = l.get();
r = 4.0;
maxspeed = ms;
maxforce = mf;
acceleration = ,);
velocity = );
}
void run() {
update();
borders();
render();
}
void follow(Path p) {
// 获取当前位置指向的任意距离的位置,现在是25
PVector predict = velocity.get();
predict.normalize();
predict.mult();
PVector predictLoc = location.get();
predictLoc.add(predict);
PVector normal = null;
PVector target = null;
;
; i < p.points.size() - ; i++) {
PVector a = p.points.get(i);
PVector b = p.points.);
// 计算线上的法线点
PVector normalPoint = getNormalPoint(predictLoc,a,b);
if(normalPoint.x < a.x || normalPoint.x > b.x) {
normalPoint = b.get();
}
float distance = predictLoc.dist(normalPoint);
if(distance < worldRecord) {
worldRecord = distance;
normal = normalPoint;
PVector dir = a.get();
dir.sub(b);
dir.normalize();
dir.mult();
target = normalPoint.get();
target.add(dir);
}
}
if(worldRecord > p.radius) {
seek(target);
}
if(debug) {
fill();
stroke();
line(location.x,location.y,predictLoc.x,predictLoc.y);
ellipse(predictLoc.x,predictLoc.y,,);
stroke();
fill();
ellipse(normal.x,normal.y,,);
line(predictLoc.x,predictLoc.y,normal.x,normal.y);
if(worldRecord > p.radius) {
fill(,,);
}
noStroke();
ellipse(target.x,target.y,,);
}
}
PVector getNormalPoint(PVector p,PVector a,PVector b) {
PVector ap = p.get();
ap.sub(a);
PVector ab = b.get();
ab.sub(a);
// 计算标量投影
ab.normalize();
ab.mult(ap.dot(ab));
PVector normalPoint = a.get();
normalPoint.add(ab);
return normalPoint;
}
void update() {
velocity.add(acceleration);
velocity.limit(maxspeed);
location.add(velocity);
acceleration.mult();
}
void applyForce(PVector force) {
acceleration.add(force);
}
void seek(PVector target) {
PVector desired = target.get();
desired.sub(location);
) {
return;
}
desired.normalize();
desired.mult(maxspeed);
PVector steer = desired.get();
desired.sub(velocity);
steer.limit(maxforce);
applyForce(steer);
}
void render() {
);
fill();
stroke();
pushMatrix();
translate(location.x,location.y);
rotate(theta);
beginShape(PConstants.TRIANGLES);
vertex(, -r * );
vertex(-r,r * );
vertex(r, r * );
endShape();
popMatrix();
}
void borders() {
if(location.x < - r) {
location.x = width + r;
}
if(location.x > width + r) {
location.x = -r;
}
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
float dot(PVector v) {
return x * v.x + y * v.y;
}
float angleBetween(PVector v2) {
float dot = this.dot(v2);
float theta = (float)Math.acos(dot / (this.mag() * v2.mag()));
return theta;
}
float dist(PVector v) {
PVector dist = this.get();
dist.sub(v);
return dist.mag();
}
}
6.10 复杂系统
什么是复杂系统?复杂系统通常是这么定义的:"一个复杂系统的整体不等同于局部的简单组合"复杂系统的局部是很简单且易于理解的个体,但它们组成的整体会表现得非常复杂,智能且难以预测.复杂系统有3个主要原则
个体之间存在小范围的联系
个体的动作是并行的
系统在整体上会呈现一种自发现象
个体之间的交互会出现复杂行为和智能模式.自然界的复杂系统确实会呈现特定的模式(蚁群,白蚁,迁移,地震,雪花,等等)
以下3个附加特性有助于我们更好地讨论复杂系统,我们可以按照这些特性完善复杂系统的模拟.需要注意的是,它们是一个模糊子集.并非所有复杂系统都具备这3个特性
非线性
竞争和合作
复杂系统的元素之间往往同时存在竞争和合作关系.后面的群集系统将引入3个规则:协调,一致和分离.协调和一致使个体相互"合作"--也就是聚集在一起并共同移动;分离使个人为空间展开"竞争"
在实现群集系统时,如果去掉竞争或合作规则,系统的复杂性可能随之丧失,竞争和合作规则存在于有生命的复杂系统中,不存在于无生命的复杂系统中,比如气候系统
反馈
复杂的系统通常包括一个反馈回路,系统的输出被反馈回系统,在正方向或反方向上影响自身行为.
6.11 群体行为(不要碰到对方)
分离指的是"从其他个体上分开",其他个体指的是列表中的其他小车
Reynolds提到:"用转向避免拥堵",也就是说,如果某辆小车和你的距离太近,你应该转向以远离它."寻找行为"指的是朝着目标转向,将"寻找行为"的转向力反转,就能得到躲避行为的转向力


ArrayList<Vehicle> vehicles;
void setup() {
size(,);
smooth();
vehicles = new ArrayList<Vehicle>();
; i < ; i++) {
vehicles.add(new Vehicle(random(width),random(height)));
}
}
void draw() {
background();
for (Vehicle v : vehicles) {
v.separate(vehicles);
v.update();
v.borders();
v.display();
}
fill();
}
void mouseDragged() {
vehicles.add(new Vehicle(mouseX,mouseY));
}
class Vehicle {
PVector location;
PVector velocity;
PVector acceleration;
float r;
float maxforce;
float maxspeed;
Vehicle(float x, float y) {
location = new PVector(x, y);
r = ;
maxspeed = ;
maxforce = 0.2;
acceleration = , );
velocity = , );
}
void applyForce(PVector force) {
acceleration.add(force);
}
void separate (ArrayList<Vehicle> vehicles) {
;
PVector sum = new PVector();
;
for (Vehicle other : vehicles) {
float d = location.get().dist(other.location);
) && (d < desiredseparation)) {
PVector diff = location.get();
diff.sub(other.location);
diff.normalize();
// 计算小车和其他小车之间的距离,距离越近,分离的幅度越大
// 距离越远,分离的幅度越小.因此我们将向量除以距离
diff.div(d);
sum.add(diff);
count++;
}
}
) {
sum.div(count);
sum.normalize();
sum.mult(maxspeed);
PVector steer = sum.get();
steer.sub(velocity);
steer.limit(maxforce);
applyForce(steer);
}
}
void update() {
velocity.add(acceleration);
velocity.limit(maxspeed);
location.add(velocity);
acceleration.mult();
}
void display() {
fill();
stroke();
pushMatrix();
translate(location.x, location.y);
ellipse(, , r, r);
popMatrix();
}
void borders() {
if (location.x < -r) location.x = width+r;
if (location.y < -r) location.y = height+r;
if (location.x > width+r) location.x = -r;
if (location.y > height+r) location.y = -r;
}
}
class PVector {
float x;
float y;
PVector() {
x = ;
y = ;
}
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
float dot(PVector v) {
return x * v.x + y * v.y;
}
float angleBetween(PVector v2) {
float dot = this.dot(v2);
float theta = (float)Math.acos(dot / (this.mag() * v2.mag()));
return theta;
}
float dist(PVector v) {
PVector dist = this.get();
dist.sub(v);
return dist.mag();
}
}
6.12 结合
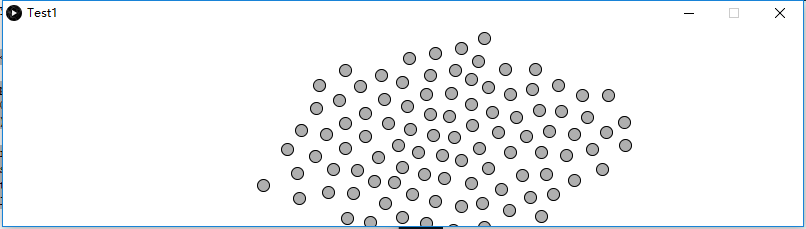
ArrayList<Vehicle> vehicles;
void setup() {
size(,);
smooth();
vehicles = new ArrayList<Vehicle>();
; i < ; i++) {
vehicles.add(new Vehicle(random(width),random(height)));
}
}
void draw() {
background();
for (Vehicle v : vehicles) {
v.applyBehaviors(vehicles);
v.update();
v.display();
}
fill();
}
void mouseDragged() {
vehicles.add(new Vehicle(mouseX,mouseY));
}
class Vehicle {
PVector location;
PVector velocity;
PVector acceleration;
float r;
float maxforce;
float maxspeed;
Vehicle(float x, float y) {
location = new PVector(x, y);
r = ;
maxspeed = ;
maxforce = 0.2;
acceleration = , );
velocity = , );
}
void applyForce(PVector force) {
acceleration.add(force);
}
void applyBehaviors(ArrayList<Vehicle> vehicles) {
PVector separateForce = separate(vehicles);
PVector seekForce = seek(new PVector(mouseX,mouseY));
separateForce.mult();
seekForce.mult();
applyForce(separateForce);
applyForce(seekForce);
}
PVector seek(PVector target) {
PVector desired = target.get();
desired.sub(location);
desired.normalize();
desired.mult(maxspeed);
PVector steer = desired.get();
steer.sub(velocity);
steer.limit(maxforce);
return steer;
}
PVector separate (ArrayList<Vehicle> vehicles) {
;
PVector sum = new PVector();
;
for (Vehicle other : vehicles) {
float d = location.get().dist(other.location);
) && (d < desiredseparation)) {
PVector diff = location.get();
diff.sub(other.location);
diff.normalize();
diff.div(d);
sum.add(diff);
count++;
}
}
) {
sum.div(count);
sum.normalize();
sum.mult(maxspeed);
sum.sub(velocity);
sum.limit(maxforce);
}
return sum;
}
void update() {
velocity.add(acceleration);
velocity.limit(maxspeed);
location.add(velocity);
acceleration.mult();
}
void display() {
fill();
stroke();
pushMatrix();
translate(location.x, location.y);
ellipse(, , r, r);
popMatrix();
}
}
class PVector {
float x;
float y;
PVector() {
x = ;
y = ;
}
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
float dot(PVector v) {
return x * v.x + y * v.y;
}
float angleBetween(PVector v2) {
float dot = this.dot(v2);
float theta = (float)Math.acos(dot / (this.mag() * v2.mag()));
return theta;
}
float dist(PVector v) {
PVector dist = this.get();
dist.sub(v);
return dist.mag();
}
}
6.13 群集
Reynolds当时使用"boid"描述群集系统中的元素("boid"是编造出来的单词,指代类似鸟类的对象);
群集有3个规则
1.分离(又叫"躲避")[separate] 避免与邻居发生碰撞
2.对齐(又叫"复制")[align] 转向力的方向和邻居保持一致
3.聚集(又叫"集中")[cohesion] 朝着邻居的中心转向(留在群体内)
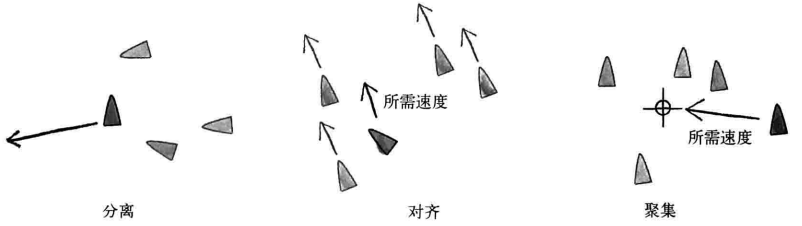



复杂系统有一个重要原则,就是元素(本例的Boid对象)之间具有短程关系.想象有一群蚂蚁,一只蚂蚁能很容易地感知它周围的环境,但却无法感知几百英尺外的其他蚂蚁.蚂蚁只能根据邻居关系执行集体行为.
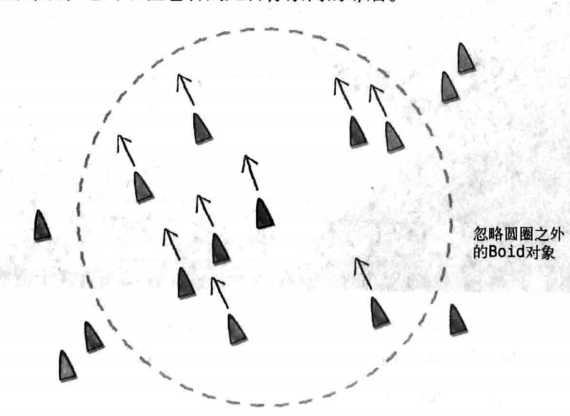

Flock flock;
void setup() {
size(,);
flock = new Flock();
; i < ; i++) {
Boid b = ,height/);
flock.addBoid(b);
}
smooth();
}
void draw() {
background();
flock.run();
fill();
}
void mouseDragged() {
flock.addBoid(new Boid(mouseX,mouseY));
}
class Flock {
ArrayList<Boid> boids;
Flock() {
boids = new ArrayList<Boid>();
}
void run() {
for (Boid b : boids) {
b.run(boids);
}
}
void addBoid(Boid b) {
boids.add(b);
}
}
class Boid {
PVector location;
PVector velocity;
PVector acceleration;
float r;
float maxforce;
float maxspeed;
color c;
Boid(float x, float y) {
acceleration = ,);
velocity = ,),random(-,));
location = new PVector(x,y);
r = 3.0;
maxspeed = ;
maxforce = 0.05;
c = color(random(),random(),random());
}
void run(ArrayList<Boid> boids) {
flock(boids);
update();
borders();
render();
}
void applyForce(PVector force) {
acceleration.add(force);
}
void flock(ArrayList<Boid> boids) {
PVector sep = separate(boids);
PVector ali = align(boids);
PVector coh = cohesion(boids);
sep.mult(1.5);
ali.mult(1.0);
coh.mult(1.0);
applyForce(sep);
applyForce(ali);
applyForce(coh);
}
void update() {
velocity.add(acceleration);
velocity.limit(maxspeed);
location.add(velocity);
acceleration.mult();
}
PVector seek(PVector target) {
PVector desired = target.get();
desired.sub(location);
desired.normalize();
desired.mult(maxspeed);
PVector steer = desired.get();
steer.sub(velocity);
steer.limit(maxforce);
return steer;
}
void render() {
);
fill(c);
stroke();
pushMatrix();
translate(location.x,location.y);
rotate(theta);
beginShape(TRIANGLES);
vertex(, -r*);
vertex(-r, r*);
vertex(r, r*);
endShape();
popMatrix();
}
void borders() {
if (location.x < -r) location.x = width+r;
if (location.y < -r) location.y = height+r;
if (location.x > width+r) location.x = -r;
if (location.y > height+r) location.y = -r;
}
PVector separate (ArrayList<Boid> boids) {
float desiredseparation = 25.0f;
PVector steer = ,);
;
for (Boid other : boids) {
float d = location.get().dist(other.location);
) && (d < desiredseparation)) {
PVector diff = location.get();
diff.sub(other.location);
diff.normalize();
diff.div(d);
steer.add(diff);
count++;
}
}
) {
steer.div((float)count);
}
) {
steer.normalize();
steer.mult(maxspeed);
steer.sub(velocity);
steer.limit(maxforce);
}
return steer;
}
PVector align (ArrayList<Boid> boids) {
;
PVector sum = ,);
;
for (Boid other : boids) {
float d = location.get().dist(other.location);
) && (d < neighbordist)) {
sum.add(other.velocity);
count++;
}
}
) {
sum.div((float)count);
sum.normalize();
sum.mult(maxspeed);
PVector steer = sum.get();
steer.sub(velocity);
steer.limit(maxforce);
return steer;
} else {
,);
}
}
PVector cohesion (ArrayList<Boid> boids) {
;
PVector sum = ,);
;
for (Boid other : boids) {
float d = location.get().dist(other.location);
) && (d < neighbordist)) {
sum.add(other.location);
count++;
}
}
) {
sum.div(count);
return seek(sum);
} else {
,);
}
}
}
class PVector {
float x;
float y;
PVector() {
x = ;
y = ;
}
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
float dot(PVector v) {
return x * v.x + y * v.y;
}
float angleBetween(PVector v2) {
float dot = this.dot(v2);
float theta = (float)Math.acos(dot / (this.mag() * v2.mag()));
return theta;
}
float dist(PVector v) {
PVector dist = this.get();
dist.sub(v);
return dist.mag();
}
}
6.14 算法效率(为什么程序跑得那么慢)

网格空间分割(bin-lattice spatial subdivison)
6.15 最后的几个注意事项:优化技巧
6.15.1 长度的平方(或距离的平方)
magSq()函数计算的是长度平方
float magSq() {
return x * x + y * y;
}
6.15.2 正弦余弦查询表
];
];
; i < ; i++) {
sinvalues[i] = sin(radians(i));
cosvalues[i] = cos(radians(i));
}
int angle = int(degrees(PI));
float answer = sinvalues[angle];
6.15.3 创建不必要的PVector对象
第7章 细胞自动机
7.1 什么是细胞自动机
术语细胞自动机的英文"cellular automata" 是复数形式,"cellular automaton" 是单数形式.为了简化,我们用"CA"表示细胞自动机
细胞自动机是由"细胞"对象组成的系统,它具有以下特性:
细胞存在于网格中(示例中是一维和二维细胞自动机,但细胞自动机可以存在于任意数量的维度中)
每个细胞都有一个状态,但可能出现的状态数量是有限的,最简单的情况就是1和0(可以称为"开"和"关",或者"生"和"死")
每个细胞都有邻居,定义"邻居"的方式有多种,通常指邻近的细胞

7.2 初等细胞自动机
CA三大要素
网格 最简单的网格是一维的,即一行细胞

状态集 最简单的状态集(多于一种状态)是0或1

邻居 在最简单的情况下,某个细胞在一维空间中的邻居就是它自身和相邻的两个细胞,即左边和右边的细胞


细胞自动机最重要的工作细节-时间,它不是现实世界的时间,而是CA运行所需的时间段,也可以称为代(generation),在本例中,时间就是动画的帧数

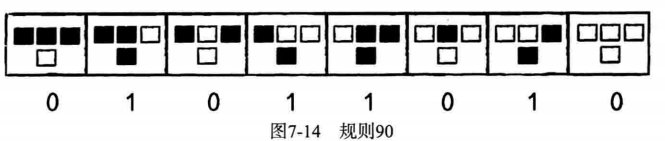
7.3 如何编写初等细胞自动机
7.4 绘制初等CA

CA ca;
void setup() {
size(,);
background();
ca = new CA();
}
void draw() {
ca.display();
if(ca.generation < height / ca.w) {
ca.generate();
}
}
class CA {
int[] cells;
int generation;
,,,,,,,};
;
CA() {
cells = new int[width / w];
; i < cells.length; i++) {
cells[i] = ;
}
cells[cells.length / ] = ;
generation = ;
}
void generate() {
int[] nextgen = new int[cells.length];
; i < cells.length - ; i++) {
];
int me = cells[i];
];
nextgen[i] = rules(left,me,right);
}
cells = nextgen;
generation++;
}
void display() {
; i < cells.length; i++) {
) fill();
);
noStroke();
rect(i * w,generation * w,w,w);
}
}
int rules(int a,int b,int c) {
&& b == && c == ) ];
&& b == && c == ) ];
&& b == && c == ) ];
&& b == && c == ) ];
&& b == && c == ) ];
&& b == && c == ) ];
&& b == && c == ) ];
&& b == && c == ) ];
;
}
}
7.5 Wolfram 分类
类别1:统一,经过若干次迭代之后,类别1的细胞状态变成了常量.这样的结果不会让人眼前一亮.

类别2:重复,和类别1相似,类别2最后也会保持稳定,但每个细胞的状态并不是常量.相反它们的状态在0和1之间来回变化
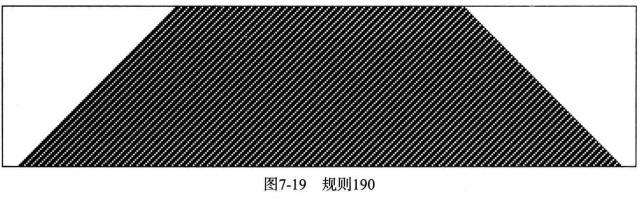
类别3:随机 这类CA的状态变化是随机的.我们无法摸清其规律.在Wolfram的Mathematica软件中,规则30被用作随机数生成器

类别4:复杂 类别4可以当作类别2和类别3的混合,其中有重复和交替的图案,但这些图案的出现是不可预测的,并且表面上看起来是随机的

7.6 生命游戏
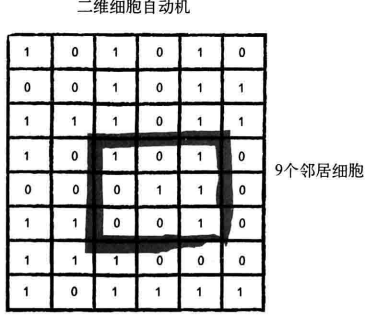
生命游戏的生存规则类似于以下问题:周围的个体数量是否过剩,是否被死亡的个体包围,还是刚刚好?
1.死亡 如果某个细胞处于"活着"状态(状态为1),在以下情况下,将会变成"死亡"状态(状态变为0)
群体过剩 如果细胞有4个及以上的邻居处于"活着"状态,则该细胞死亡
孤独 如果"活着"的邻居数量等于或少于1个,则细胞死亡
2.新生 处于"死亡"状态(状态为0)的细胞,如果它周围刚好有3个"活着"的邻居,则它也会变为"活着"状态
3.静止 在其他情况下,细胞的状态保持不变.
保持"活着" 如果细胞是"活着"的,而且周围有2个或3个或者的邻居,它将继续"活着"
保持"死亡" 如果细胞是"死亡"的,而且周围"活着"的邻居数不等于3,它将继续保持"死亡"状态
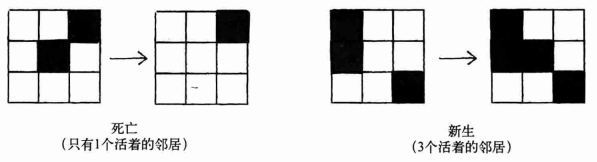
7.7 编写生命游戏
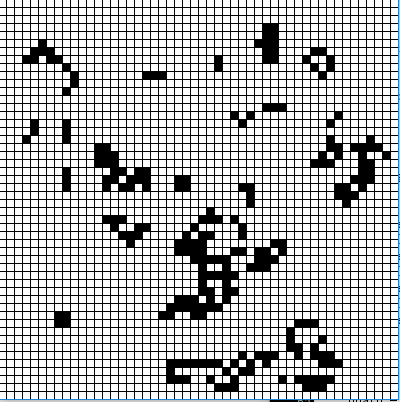
GOL gol;
void setup() {
size(,);
gol = new GOL();
}
void draw() {
background();
gol.generate();
gol.display();
}
void mousePressed() {
gol.init();
}
class GOL {
;
int columns,rows;
int[][] board;
GOL() {
columns = width / w;
rows = height / w;
board = new int[columns][rows];
init();
}
void init() {
; i < columns - ; i++) {
; j < rows - ; j++) {
board[i][j] = ));
}
}
}
void generate() {
int[][] next = new int[columns][rows];
; x < columns - ; x++) {
; y < rows - ; y++) {
;
; i <= ; i++) {
; j <= ; j++) {
neighbors += board[x + i][y + j];
}
}
neighbors -= board[x][y];
) && (neighbors < )) { // 孤独
next[x][y] = ;
} ) && (neighbors > )) { // 群体过剩
next[x][y] = ;
} ) && (neighbors == )) { // 新生
next[x][y] = ;
} else { // 静止
next[x][y] = board[x][y];
}
}
}
board = next;
}
void display() {
; i < columns; i++) {
; j < rows; j++) {
) {
fill();
} else {
fill();
}
stroke();
rect(i * w,j * w,w,w);
}
}
}
}
7.8 面向对象的细胞实现
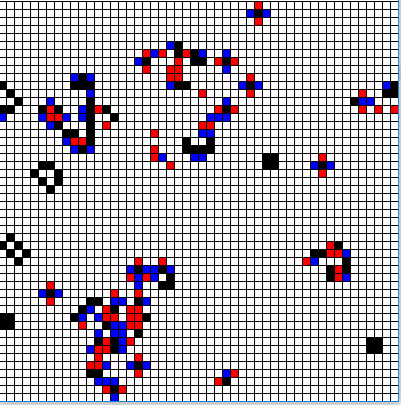
GOL gol;
void setup() {
size(, );
smooth();
gol = new GOL();
}
void draw() {
background();
gol.generate();
gol.display();
}
// reset board when mouse is pressed
void mousePressed() {
gol.init();
}
class GOL {
;
int columns, rows;
// Game of life board
Cell[][] board;
GOL() {
// Initialize rows, columns and set-up arrays
columns = width/w;
rows = height/w;
board = new Cell[columns][rows];
init();
}
void init() {
; i < columns; i++) {
; j < rows; j++) {
board[i][j] = new Cell(i*w, j*w, w);
}
}
}
// The process of creating the new generation
void generate() {
; i < columns;i++) {
; j < rows;j++) {
board[i][j].savePrevious();
}
}
// Loop through every spot in our 2D array and check spots neighbors
; x < columns; x++) {
; y < rows; y++) {
// Add up all the states in a 3x3 surrounding grid
;
; i <= ; i++) {
; j <= ; j++) {
neighbors += board[(x+i+columns)%columns][(y+j+rows)%rows].previous;
}
}
// A little trick to subtract the current cell's state since
// we added it in the above loop
neighbors -= board[x][y].previous;
// Rules of Life
) && (neighbors < )) board[x][y].newState(); // Loneliness
) && (neighbors > )) board[x][y].newState(); // Overpopulation
) && (neighbors == )) board[x][y].newState(); // Reproduction
// else do nothing!
}
}
}
// This is the easy part, just draw the cells, fill 255 for '1', fill 0 for '0'
void display() {
; i < columns;i++) {
; j < rows;j++) {
board[i][j].display();
}
}
}
}
class Cell {
float x, y;
float w;
int state;
int previous;
Cell(float x_, float y_, float w_) {
x = x_;
y = y_;
w = w_;
state = ));
previous = state;
}
void savePrevious() {
previous = state;
}
void newState(int s) {
state = s;
}
void display() {
&& state == ) fill(,,);
) fill();
&& state == ) fill(,,);
);
stroke();
rect(x, y, w, w);
}
}
7.9 传统CA的变化
第8章 分形
8.1 什么是分形
术语分形(源自拉丁文fractus,意思是"破碎")是数学家本华*曼德博(Benoit Mandelbrot)于1975年提出的.在他的<<大自然的分形几何>>(The Fractal Geometry of Natrue)中,分形被定义为"一个粗糙或零碎的几何形状,可以分成数个部分,且每一部分都是整体缩小后的形状(至少近似)"

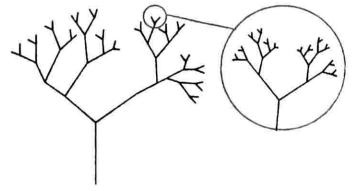
自相似,每一部分都是"整体缩小后的形状"
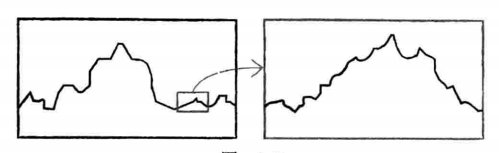
随机分形指的是根据概率和随机性构建的分形.不同于确定性的树形结构,随机分形只是在数据上有自相似的特性
尽管自相似是分形的重要特征,但你需要认识到,单纯的自相似并不能构成分形.一条直线也具有自相似的特征,它在任意缩放尺度下看起来都是一样的,而且可以看成是由无数短直线构成的,但直线并不是分形
分形的特点是在小尺度下也有精细的结构,而且这个结构不能用欧氏几何描述.如果你可以说"这是一条直线!",那么这就不是一个分形.
8.2 递归

把一条线段分成两条线段,把得到的线段再分成两条,最终得到4条线段.再将同样的规则作用在这4条线段上,你会得到8条线段.这种连续地在结果上重复应用某条规则的过程就称为递归
调用自身的函数称为递归函数
所有的递归函数都必须有一个退出条件
void setup() {
size(,);
smooth();
}
void draw() {
background();
drawCircle(width/,height/,width);
noLoop();
}
void drawCircle(int x, int y, float r) {
ellipse(x, y, r, r);
) {
r *= 0.75f;
drawCircle(x, y, r);
}
}
void setup() {
size(,);
}
void draw() {
background();
drawCircle(width / ,height / ,);
}
void drawCircle(float x,float y,float radius) {
stroke();
noFill();
ellipse(x,y,radius,radius);
) {
drawCircle(x + radius / ,y,radius / );
drawCircle(x - radius / ,y,radius / );
}
}

void setup() {
size(,);
}
void draw() {
background();
drawCircle(width / ,height / ,);
}
void drawCircle(float x,float y,float radius) {
stroke();
noFill();
ellipse(x,y,radius,radius);
) {
drawCircle(x + radius / ,y,radius / );
drawCircle(x - radius / ,y,radius / );
drawCircle(x,y + radius / ,radius / );
drawCircle(x,y - radius / ,radius / );
}
}
8.3 用递归函数实现康托尔集

void setup() {
size(,);
background();
cantor(,,);
}
void draw() {
noLoop();
}
void cantor(float x,float y,float len) {
;
) {
noStroke();
fill();
rect(x,y,len,h / );
y += h;
cantor(x,y,len / );
cantor(x + len * / ,y,len / );
}
}
8.4 科赫曲线和ArrayList技术
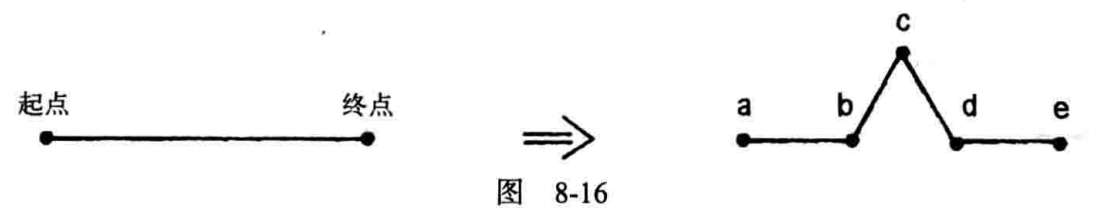

ArrayList<KochLine> lines ;
void setup() {
size(, );
background();
lines = new ArrayList<KochLine>();
PVector start = , );
PVector end = );
lines.add(new KochLine(start, end));
smooth();
}
void draw() {
background();
for (KochLine l : lines) {
l.display();
}
}
void mousePressed() {
generate();
}
void generate() {
ArrayList next = new ArrayList<KochLine>();
for (KochLine l : lines) {
PVector a = l.kochA();
PVector b = l.kochB();
PVector c = l.kochC();
PVector d = l.kochD();
PVector e = l.kochE();
next.add(new KochLine(a, b));
next.add(new KochLine(b, c));
next.add(new KochLine(c, d));
next.add(new KochLine(d, e));
}
lines = next;
}
class KochLine {
PVector start;
PVector end;
KochLine(PVector a, PVector b) {
start = a.get();
end = b.get();
}
void display() {
stroke();
line(start.x, start.y, end.x, end.y);
}
PVector kochA() {
return start.get();
}
PVector kochB() {
PVector v = end.get();
v.sub(start);
v.div();
v.add(start);
return v;
}
PVector kochC() {
PVector a = start.get();
PVector v = end.get();
v.sub(start);
v.div();
a.add(v);
rotate(v, -radians());
a.add(v);
return a;
}
PVector kochD() {
PVector v = end.get();
v.sub(start);
v.mult(/3.0);
v.add(start);
return v;
}
PVector kochE() {
return end.get();
}
void rotate(PVector v, float theta) {
float xTemp = v.x;
v.x = v.x * cos(theta) - v.y * sin(theta);
v.y = xTemp * sin(theta) + v.y * cos(theta);
}
}
class PVector {
float x;
float y;
PVector() {
x = ;
y = ;
}
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
float dot(PVector v) {
return x * v.x + y * v.y;
}
float angleBetween(PVector v2) {
float dot = this.dot(v2);
float theta = (float)Math.acos(dot / (this.mag() * v2.mag()));
return theta;
}
float dist(PVector v) {
PVector dist = this.get();
dist.sub(v);
return dist.mag();
}
}
8.5 树

float theta;
void setup() {
size(,);
}
void draw() {
background();
theta = map(mouseX,,width,,PI / );
translate(width / ,height);
stroke();
branch();
}
void branch(float len) {
strokeWeight();
line(,,,-len);
translate(,-len);
len *= 0.66;
) {
pushMatrix();
rotate(theta);
branch(len);
popMatrix();
pushMatrix();
rotate(-theta);
branch(len);
popMatrix();
}
}
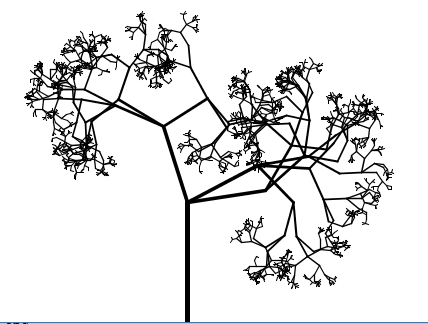
void setup() {
size(, );
smooth();
newTree();
}
void draw() {
}
void mousePressed() {
newTree();
}
void newTree() {
background();
fill();
stroke();
translate(width / , height);
branch();
}
void branch(float h) {
, , , );
strokeWeight(sw);
line(, , , -h);
translate(, -h);
h *= 0.66f;
) {
, ));
; i < n; i++) {
, PI/);
pushMatrix();
rotate(theta);
branch(h);
popMatrix();
}
}
}
8.6 L系统
1968年,匈牙利植物学家Aristid Lindenmayer开发出了一套基于语法的系统,用于模拟植物的生长模式.这套系统称作L系统(Lindenmayer系统的简称).
一个L系统主要包括3个元素
字母表 L系统的字母表由系统可能出现的合法字符组成.比如字母表"ABC",意思是L系统中的任何"语句"(由字符组成串)只能包含这3个字符
公理 公理是一个语句,用于描述系统的初始状态.举个例子,对于字母表为"ABC"的L系统,它的公理可以是"AAA""B"或"ACBAB"
规则 L系统的规则首先作用于公理,然后递归作用于结果,每次作用都会产生一个|新的语句.一个规则包括"前身"和"继任者"两部分.比如,规则"A->AB"的意思就是:把字符串中的所有"A"都替换成"AB".
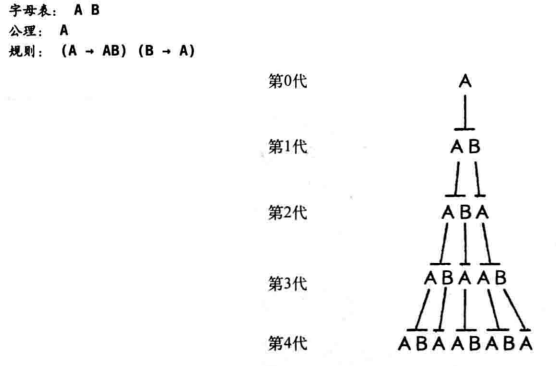
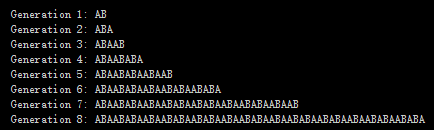
String current = "A";
;
void setup() {
size(, );
}
void draw() {
background();
fill();
noLoop();
}
void mousePressed() {
StringBuffer next = new StringBuffer();
; i < current.length(); i++) {
char c = current.charAt(i);
if (c == 'A') {
next.append("AB");
} else if (c == 'B') {
next.append("A");
}
}
current = next.toString();
count++;
println("Generation " + count + ": " + current);
}

LSystem lsys;
Turtle turtle;
void setup() {
size(, );
Rule[] ruleset = ];
ruleset[] = new Rule('F', "FF+[+F-F-F]-[-F+F+F]");
lsys = new LSystem("F", ruleset);
turtle = , radians());
smooth();
}
void draw() {
background();
fill();
translate(width/, height);
rotate(-PI/);
turtle.render();
noLoop();
}
;
void mousePressed() {
) {
pushMatrix();
lsys.generate();
turtle.setToDo(lsys.getSentence());
turtle.changeLen(0.5);
popMatrix();
redraw();
counter++;
}
}
class LSystem {
String sentence;
Rule[] ruleset;
int generation;
LSystem(String axiom, Rule[] r) {
sentence = axiom;
ruleset = r;
generation = ;
}
void generate() {
StringBuffer nextgen = new StringBuffer();
; i < sentence.length(); i++) {
char curr = sentence.charAt(i);
String replace = "" + curr;
; j < ruleset.length; j++) {
char a = ruleset[j].getA();
if (a == curr) {
replace = ruleset[j].getB();
break;
}
}
nextgen.append(replace);
}
sentence = nextgen.toString();
generation++;
}
String getSentence() {
return sentence;
}
int getGeneration() {
return generation;
}
}
class Rule {
char a;
String b;
Rule(char a_, String b_) {
a = a_;
b = b_;
}
char getA() {
return a;
}
String getB() {
return b;
}
}
class Turtle {
String todo;
float len;
float theta;
Turtle(String s, float l, float t) {
todo = s;
len = l;
theta = t;
}
void render() {
stroke(,);
; i < todo.length(); i++) {
char c = todo.charAt(i);
if (c == 'F' || c == 'G') {
line(,,len,);
translate(len,);
}
else if (c == '+') {
rotate(theta);
}
else if (c == '-') {
rotate(-theta);
}
else if (c == '[') {
pushMatrix();
}
else if (c == ']') {
popMatrix();
}
}
}
void setLen(float l) {
len = l;
}
void changeLen(float percent) {
len *= percent;
}
void setToDo(String s) {
todo = s;
}
}
第9章 代码的进化
9.1 遗传算法:启发自真实现象
9.2 为什么使用遗传算法
9.3 达尔文的自然选择
如果要正确地模拟自然选择,我们必须同时实现达尔文进化学中的3个基本法则
1.遗传 子代必须以某种方式继承父代的特性.如果生物存活的时间足够长,繁殖的概率也足够大,那么它们的特征将会传递给下一代
2.突变 种群的个体具有多种特征,也就是说,必须引入突变的机制保证个体的多样化
3.选择 必须有一种选择机制:使得种群中的某些个体能够繁殖,把自己的基因传递给下一代;而另一些个体却没有机会繁殖.这通常称作"适者生存".
9.4 遗传算法,第一部分:创建种群
继续猴子敲键盘的例子,我们将为此创建一个由句子构成的种群("句子"指的是一个字符串)
创建一个种群,用随机的方式生成种群内的个体
本章的种群个体拥有虚拟的"DNA",DNA是描述个体外形和行为的一系列属性(我们称为"基因"),比如,在猴子敲键盘的例子中,DNA就是字符串
遗传领域有两个重要概念:基因型和表现型,两者之间有重要区别.基因型(genotype)就是遗传密码,也就是本例的字符串,它会从父代传给子代;表现型(phenotype)就是基因型的表达.两者之间的区别关系着遗传算法的实现.
在图形编程中,我们一直在回答以下问题:你的世界是由什么对象组成的,以及如何设计这些对象的基因型(存储对象属性的数据结构)和表现型(你想用这些对象表达什么).


总结:创建由N个个体组成的种群,每个个体都有随机的DNA
9.5 遗传算法,第二部分:选择
选择过程需要评估种群个体的适应度,从而选出更适合繁殖的个体.我们可以将选择过程分为两部分
1.评估适应度
为了让遗传算法有效,我们需要设计一个适应度函数.这个函数会产生一个描述个体适应度的分值.当然,现实世界并不是这么运作的.在现实世界中,生物并没有分值,它们只有两种选择:生存或死亡.但传统遗传算法的最终目的是进化出最佳方案,所以它需要用分值衡量每一种方案的效果

2.创建交配池
得到所有个体的适应度后,我们就开始选择合适的个体,并将它们放入交配池.这一步的实现方式有很多种.可以只选择个体中的精英:"哪两个个体的分数是最高的?所有后代都将由这两个个体繁殖出来!"在编程实现上,这是最简单的方案,但它不符合多样性原则.如果种群(可能由上千个个体组成)中的两个个体成了唯一的繁殖个体,那么下一代的多样性就会非常低,这会抑制种群的进化过程.也可以扩大交配池中的个体数量--比如,前50%的个体都能繁殖后代,也就是说,如果有1000个个体,那么前500个能繁殖后代.这种方案也很容易实现,但不会产生最优的结果.在这种情况下,排名靠前的个体的繁殖机会和排在中间的个体一样.为什么排在第500位的个体有繁殖机会,而排在第501位的个体却没有繁殖机会呢?
一种更好的方案是概率方法,我们称为"命运之轮"(又叫作"赌盘")



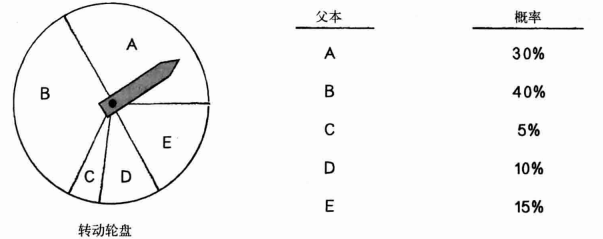
转到这个轮盘,你会发现B被选中的概率最大,接下来是A,然后是D和E,最后是C.基于概率的选择方法是一种很好的实现方式:首先,它保证概率最高的个体有最大的繁殖机会;其次,它并不会减弱种群的多样性,和精英选择的方式有所不同,即使是最低分值的个体(C)依然有把基因传给后代的机会.低分值的个体可能有一些非常有用的基因片段,这些片段不能被移除.比如,在"to be or not to be"的进化过程中,可能会出现以下个体

你可以看出,A和B是适应度最高的个体.但是它们都不是最优解,因为它们的最后两个字符都不正确.尽管C的分值很低,但它最后的基因片段恰好是正确的.因此,尽管我们要用A和B产生大部分的后代基因,却仍需要让C有机会参与繁殖过程
9.6 遗传算法,第三部分:繁殖
现在我们已经有了选择父代的策略,下面就开始讨论繁殖下一代的方法,这一步的关键在于达尔文的遗传法则--子代能继承父代的特性.繁殖的实现方式也有很多种.无性繁殖就是一种合理(并容易实现)的策略,该策略用单个父本复制出子代个体.但遗传算法的标准方法是用两个父本繁殖后代
1.交叉
交叉就是根据双亲的遗传密码创建一个子代

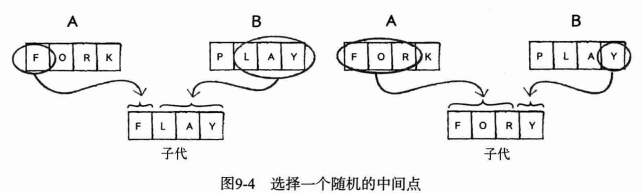
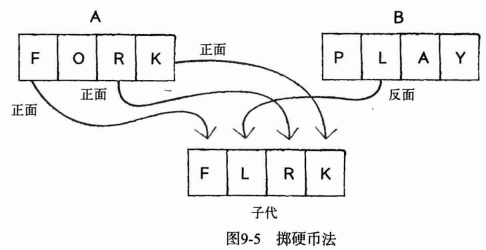
2.突变
交叉过程产生子代DNA,但还要经历突变过程猜能最终确定.突变是一个可选的过程,某些场景不会涉及突变.根据达尔文的进化学说,突变是普遍存在的.在初始化过程中,我们用随机的方式创建种群,确保种群有一定的多样性.但在孕育第一代时,种群的多样性就已经确定了;而突变的作用就是在进化过程中不断引入多样性
突变可以用突变率描述.一个遗传算法可能有5%,1%或0.1%的突变率.假设交叉完成后,某子代个体是"FORY",如果突变率为1%,这意味着每个字符有1%的突变概率.而字符怎么发生突变呢?在本例中,我们把突变定义为用一个随机的字符替换原字符.1%是一个很低的突变率,对于由4个字符组成的字符串来说,在大部分时间它都不会发生突变(确切地说,在96%得时间都不会发生突变).一旦突变发生,当前字符就会被替换成另一个随机字符
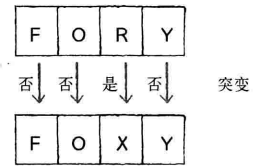
9.7 创建种群的代码
9.7.1 第1步:初始化种群
9.7.2 第2步:选择
9.7.3 第3步:繁殖
9.8 遗传算法:整合代码

float mutationRate = 0.01; // 突变几率
; // 种群大小
DNA[] population; // 种群
ArrayList<DNA> matingPool; // 交配池
String target;
PFont f;
void setup() {
size(,);
target = "to be or not to be";
population = new DNA[totalPopulation];
; i < population.length; i++) {
population[i] = new DNA(target.length());
}
f = createFont(,true);
}
void draw() {
; i < population.length; i++) {
population[i].calcFitness(target);
}
ArrayList<DNA> matingPool = new ArrayList<DNA>();
; i < population.length; i++) {
// n等于适应度乘以100,是一个介于0~100的整数
);
// 在交配池中将个体添加N次
; j < n; j++) {
matingPool.add(population[i]);
}
}
; i < population.length; i++) {
int a = int(random(matingPool.size()));
int b = int(random(matingPool.size()));
DNA partnerA = matingPool.get(a);
DNA partnerB = matingPool.get(b);
DNA child = partnerA.crossover(partnerB);
child.mutate(mutationRate);
population[i] = child;
}
background();
fill();
String everything = "";
; i < population.length; i++) {
everything += population[i].getPhrase() + " ";
}
textFont(f,);
text(everything,,,width,height);
}
class DNA {
char[] genes;
float fitness;
DNA(int num) {
genes = new char[num];
; i < genes.length; i++) {
genes[i] = (,);
}
}
void calcFitness(String target) {
;
; i < genes.length; i++) {
if(genes[i] == target.charAt(i)) {
score++;
}
}
fitness = (float)score / (float)target.length();
}
// 交叉
DNA crossover(DNA partner) {
DNA child = new DNA(genes.length);
int midpoint = int(random(genes.length));
; i < genes.length; i++) {
if(i > midpoint) {
child.genes[i] = genes[i];
} else {
child.genes[i] = partner.genes[i];
}
}
return child;
}
void mutate(float mutationRate) {
; i < genes.length; i++) {
) < mutationRate) {
genes[i] = (,);
}
}
}
String getPhrase() {
return new String(genes);
}
}
9.9 遗传算法:创建自己的遗传算法
9.9.1 第1点:更改变量
9.9.2 第2点:适应度函数
9.9.3 第3点:基因型和表现型

PFont f;
String target;
int popmax;
float mutationRate;
Population population;
void setup() {
size(,);
f = createFont(,true);
target = "To be or not to be.";
popmax = ;
mutationRate = 0.01;
population = new Population(target,mutationRate,popmax);
}
void draw() {
population.naturalSelection();
population.generate();
population.calcFitness();
displayInfo();
if(population.finished()) {
println(millis() / 1000.0);
noLoop();
}
}
void displayInfo() {
background();
String answer = population.getBest();
textFont(f);
textAlign(LEFT);
fill();
textSize();
text(,);
textSize();
text(answer,,);
textSize();
text(,);
text(,),,);
text(,);
text() + ,);
textSize();
text(,);
}
class Population {
float mutationRate;
DNA[] population;
ArrayList<DNA> matingPool;
String target;
int generations;
boolean finished;
int perfectScore;
Population(String p,float m,int num) {
target = p;
mutationRate = m;
population = new DNA[num];
; i < population.length; i++) {
population[i] = new DNA(target.length());
}
calcFitness();
matingPool = new ArrayList<DNA>();
finished = false;
generations = ;
perfectScore = ,target.length()));
}
void calcFitness() {
; i < population.length; i++) {
population[i].fitness(target);
}
}
void naturalSelection() {
matingPool.clear();
;
; i < population.length; i++) {
if(population[i].fitness > maxFitness) {
maxFitness = population[i].fitness;
}
}
; i < population.length; i++) {
,maxFitness,,);
);
; j < n; j++) {
matingPool.add(population[i]);
}
}
}
void generate() {
; i < population.length; i++) {
int a = int(random(matingPool.size()));
int b = int(random(matingPool.size()));
DNA partnerA = matingPool.get(a);
DNA partnerB = matingPool.get(b);
DNA child = partnerA.crossover(partnerB);
child.mutate(mutationRate);
population[i] = child;
}
generations++;
}
String getBest() {
float worldrecord = 0.0f;
;
; i < population.length; i++) {
if(population[i].fitness > worldrecord) {
index = i;
worldrecord = population[i].fitness;
}
}
println(worldrecord + "|" + perfectScore);
if(worldrecord == perfectScore) {
finished = true;
}
return population[index].getPhrase();
}
boolean finished() {
return finished;
}
int getGenerations() {
return generations;
}
float getAverageFitness() {
;
; i < population.length; i++) {
total += population[i].fitness;
}
return total / (population.length);
}
String allPhrases() {
String everything = "";
);
; i < displayLimit; i++) {
everything += population[i].getPhrase() + "\n";
}
return everything;
}
}
class DNA {
char[] genes;
float fitness;
DNA(int num) {
genes = new char[num];
; i < genes.length; i++) {
genes[i] = (,);
}
}
void fitness(String target) {
;
; i < genes.length; i++) {
if(genes[i] == target.charAt(i)) {
score++;
}
}
fitness = (float)score / (float)target.length();
}
// 交叉
DNA crossover(DNA partner) {
DNA child = new DNA(genes.length);
int midpoint = int(random(genes.length));
; i < genes.length; i++) {
if(i > midpoint) {
child.genes[i] = genes[i];
} else {
child.genes[i] = partner.genes[i];
}
}
return child;
}
void mutate(float mutationRate) {
; i < genes.length; i++) {
) < mutationRate) {
genes[i] = (,);
}
}
}
String getPhrase() {
return new String(genes);
}
}
9.10 力的进化:智能火箭
9.11 智能火箭:整合代码
9.12 交互式选择
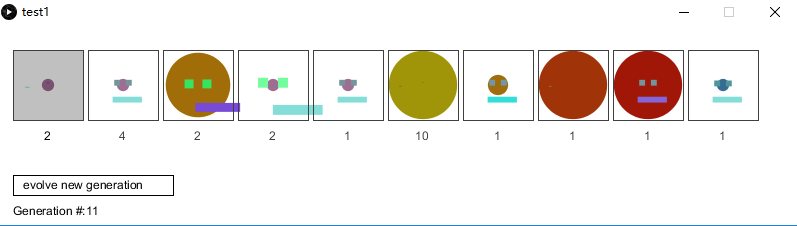
Population population;
Button button;
void setup() {
size(,);
colorMode(RGB,1.0);
smooth();
;
float mutationRate = 0.05;
population = new Population(mutationRate,popmax);
button = ,,,, "evolve new generation");
}
void draw() {
background(1.0);
population.display();
population.rollover(mouseX,mouseY);
textAlign(LEFT);
fill();
text(,);
button.display();
button.rollover(mouseX,mouseY);
}
void mousePressed() {
if (button.clicked(mouseX,mouseY)) {
population.selection();
population.reproduction();
}
}
void mouseReleased() {
button.released();
}
class Population {
float mutationRate;
Face[] population;
ArrayList<Face> matingPool;
int generations;
Population(float m, int num) {
mutationRate = m;
population = new Face[num];
matingPool = new ArrayList<Face>();
generations = ;
; i < population.length; i++) {
population[i] = +i*, );
}
}
void display() {
; i < population.length; i++) {
population[i].display();
}
}
void rollover(int mx, int my) {
; i < population.length; i++) {
population[i].rollover(mx, my);
}
}
void selection() {
matingPool.clear();
float maxFitness = getMaxFitness();
; i < population.length; i++) {
, maxFitness, , );
);
; j < n; j++) {
matingPool.add(population[i]);
}
}
}
void reproduction() {
; i < population.length; i++) {
int m = int(random(matingPool.size()));
int d = int(random(matingPool.size()));
Face mom = matingPool.get(m);
Face dad = matingPool.get(d);
DNA momgenes = mom.getDNA();
DNA dadgenes = dad.getDNA();
DNA child = momgenes.crossover(dadgenes);
child.mutate(mutationRate);
population[i] = +i*, );
}
generations++;
}
int getGenerations() {
return generations;
}
float getMaxFitness() {
;
; i < population.length; i++) {
if (population[i].getFitness() > record) {
record = population[i].getFitness();
}
}
return record;
}
}
class Face {
DNA dna;
float fitness;
float x, y;
;
boolean rolloverOn;
Rectangle r;
Face(DNA dna_, float x_, float y_) {
dna = dna_;
x = x_;
y = y_;
fitness = ;
r = ), ), int(wh), int(wh));
}
void display() {
],,,,);
color c = color(dna.genes[],dna.genes[],dna.genes[]);
],,,,);
],,,,);
],,,,);
color eyecolor = color(dna.genes[],dna.genes[],dna.genes[]);
color mouthColor = color(dna.genes[],dna.genes[],dna.genes[]);
],,,,);
],,,-,);
],,,,);
],,,,);
pushMatrix();
translate(x, y);
noStroke();
smooth();
fill(c);
ellipseMode(CENTER);
ellipse(, , r, r);
fill(eyecolor);
rectMode(CENTER);
rect(-eye_x, -eye_y, eye_size, eye_size);
rect( eye_x, -eye_y, eye_size, eye_size);
fill(mouthColor);
rectMode(CENTER);
rect(mouth_x, mouth_y, mouthw, mouthh);
stroke(0.25);
, 0.25);
else noFill();
rectMode(CENTER);
rect(, , wh, wh);
popMatrix();
textAlign(CENTER);
);
else fill(0.25);
text();
}
float getFitness() {
return fitness;
}
DNA getDNA() {
return dna;
}
void rollover(int mx, int my) {
if (r.contains(mx, my)) {
rolloverOn = true;
fitness += 0.25;
} else {
rolloverOn = false;
}
}
}
class Button {
Rectangle r;
String txt;
boolean clickedOn;
boolean rolloverOn;
Button(int x, int y, int w, int h, String s) {
r = new Rectangle(x,y,w,h);
txt = s;
}
void display() {
rectMode(CORNER);
stroke(); noFill();
if (rolloverOn) fill(0.5);
);
rect(r.x,r.y,r.width,r.height);
float b = 0.0;
;
else if (rolloverOn) b = 0.2;
;
fill(b);
textAlign(LEFT);
text(txt,r.x+,r.y+);
}
boolean rollover(int mx, int my) {
if (r.contains(mx,my)) rolloverOn = true;
else rolloverOn = false;
return rolloverOn;
}
boolean clicked(int mx, int my) {
if (r.contains(mx,my)) clickedOn = true;
return clickedOn;
}
void released() {
clickedOn = false;
}
}
class Rectangle {
int x;
int y;
int width;
int height;
Rectangle(int x_, int y_, int w, int h) {
x = x_;
y = y_;
width = w;
height = h;
}
boolean contains(int px, int py) {
return (px > x && px < x + width && py > y && py < y + height);
}
}
class DNA {
float[] genes;
;
DNA() {
genes = new float[len];
; i < genes.length; i++) {
genes[i] = random(,);
}
}
DNA(float[] newgenes) {
genes = newgenes;
}
DNA crossover(DNA partner) {
float[] child = new float[genes.length];
int crossover = int(random(genes.length));
; i < genes.length; i++) {
if (i > crossover) child[i] = genes[i];
else child[i] = partner.genes[i];
}
DNA newgenes = new DNA(child);
return newgenes;
}
void mutate(float m) {
; i < genes.length; i++) {
) < m) {
genes[i] = random(,);
}
}
}
}
9.13 生态系统模拟
9.13.1 基因型和表现型
9.13.2 选择和繁殖

World world;
void setup() {
size(, );
world = );
smooth();
}
void draw() {
background();
world.run();
}
void mousePressed() {
world.born(mouseX,mouseY);
}
class World {
ArrayList<Bloop> bloops;
Food food;
World(int num) {
food = new Food(num);
bloops = new ArrayList<Bloop>();
; i < num; i++) {
PVector l = new PVector(random(width),random(height));
DNA dna = new DNA();
bloops.add(new Bloop(l,dna));
}
}
void born(float x, float y) {
PVector l = new PVector(x,y);
DNA dna = new DNA();
bloops.add(new Bloop(l,dna));
}
void run() {
food.run();
; i >= ; i--) {
Bloop b = bloops.get(i);
b.run();
b.eat(food);
if (b.dead()) {
bloops.remove(i);
food.add(b.location);
}
Bloop child = b.reproduce();
if (child != null) bloops.add(child);
}
}
}
class Bloop {
PVector location;
DNA dna;
float health;
float xoff;
float yoff;
float r;
float maxspeed;
Bloop(PVector l, DNA dna_) {
location = l.get();
health = ;
xoff = random();
yoff = random();
dna = dna_;
maxspeed = map(dna.genes[], , , , );
r = map(dna.genes[], , , , );
}
void run() {
update();
borders();
display();
}
void eat(Food f) {
ArrayList<PVector> food = f.getFood();
; i >= ; i--) {
PVector foodLocation = food.get(i);
float d = location.dist(foodLocation);
) {
health += ;
food.remove(i);
}
}
}
Bloop reproduce() {
) < 0.0005) {
DNA childDNA = dna.copy();
childDNA.mutate(0.01);
return new Bloop(location, childDNA);
}
else {
return null;
}
}
void update() {
,,-maxspeed,maxspeed);
,,-maxspeed,maxspeed);
PVector velocity = new PVector(vx,vy);
xoff += 0.01;
yoff += 0.01;
location.add(velocity);
health -= 0.2;
}
void borders() {
if (location.x < -r) location.x = width+r;
if (location.y < -r) location.y = height+r;
if (location.x > width+r) location.x = -r;
if (location.y > height+r) location.y = -r;
}
void display() {
ellipseMode(CENTER);
stroke(,health);
fill(, health);
ellipse(location.x, location.y, r, r);
}
boolean dead() {
if (health < 0.0) {
return true;
}
else {
return false;
}
}
}
class Food {
ArrayList<PVector> food;
Food(int num) {
food = new ArrayList();
; i < num; i++) {
food.add(new PVector(random(width),random(height)));
}
}
void add(PVector l) {
food.add(l.get());
}
void run() {
for (PVector f : food) {
rectMode(CENTER);
stroke();
fill();
rect(f.x,f.y,,);
}
) < 0.001) {
food.add(new PVector(random(width),random(height)));
}
}
ArrayList getFood() {
return food;
}
}
class DNA {
float[] genes;
DNA() {
genes = ];
; i < genes.length; i++) {
genes[i] = random(,);
}
}
DNA(float[] newgenes) {
genes = newgenes;
}
DNA copy() {
float[] newgenes = new float[genes.length];
; i < newgenes.length; i++) {
newgenes[i] = genes[i];
}
return new DNA(newgenes);
}
void mutate(float m) {
; i < genes.length; i++) {
) < m) {
genes[i] = random(,);
}
}
}
}
class PVector {
float x;
float y;
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
float dot(PVector v) {
return x * v.x + y * v.y;
}
float angleBetween(PVector v2) {
float dot = this.dot(v2);
float theta = (float)Math.acos(dot / (this.mag() * v2.mag()));
return theta;
}
float dist(PVector v) {
PVector dist = this.get();
dist.sub(v);
return dist.mag();
}
}
第10章 神经网络
10.1 人工神经网络:导论和应用
1943年,神经学家Warren S.McCulloch和逻辑学家Walter Pitts共同开发了第一个概念性人工神经网络模型.在一篇名为A logical calculus of the ideas imminent in nervous activity的论文中,他们这样描述神经元:一个处在网络中的细胞,能够接收输入,然后处理这些输入,并产生输出
他们没有精确描述大脑的工作方式,后续的诸多人工神经网络研究者也是如此,人工神经网络只是一个基于大脑工作方式设计的用于解决特定问题的计算模型
神经网络最常见的应用就是执行"人类容易决绝,而计算机难以解决"的任务,这类任务通常称作模式识别.
神经网络是一个"联结"的计算系统,而我们编写的计算机程序是过程式的:程序从第一行代码开始,执行完这一行代码后就继续执行下一行,所有指令都是以线性方式组织起来的.神经网络并不遵循线性路径,相反,整个网络的节点(节点就是神经元)以并行的方式处理信息
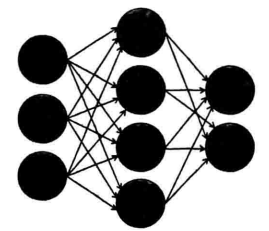
神经网络也是复杂系统的一个例子.作为神经网络的个体元素,神经元的功能非常简单,它只读取输入,处理输入信息,最后产生输出.但由诸多神经元构成的网络却能表现处极其丰富和智能的行为
神经网络的关键要素之一是它的学习能力.神经网络不只是一个复杂的系统,还是一个复杂的自适应系统.这意味着它可以根据流经的信息改变自身的内部结构,一般情况下,这个过程通过调整权重的方式实现.在上图中,每一条连线表示两个神经元之间的连接,箭头表示信息流的通过.每个连接都有自己的权重--控制两个神经元之间信号传递的数字.如果网络产生一个"好"的输出,则不需要调整权重;如果网络产生一个"差"的输出,也就是一个错误,那么系统将会执行适应过程,改变自己的内部权重,以改进后续的输出结果
神经网络的学习策略:
监督式学习 本质上,这种策略还涉及一个"老师","老师"比神经网络本身更智能.在面部识别中,"老师"向神经网络展示一系列脸部照片.神经网络先猜测这些脸的名字,随后"老师"告诉它正确答案,让神经网络比较猜测结果和"正确"答案的区别,再根据错误进行调整
非监督式学习 这种策略适用于没有已知数据集的情况,比如在一个数据集中寻找隐藏模式.聚类就是此类神经网络的一种应用,它的功能是根据未知规律对一组元素进行分组.
增强式学习 这种策略构建在观察基础上.想象一只老鼠走迷宫:如果它朝左走,会得到一块奶酪;朝右走,会受到惊吓.经过一段时间的学习后,老鼠会自觉向左转.其中的学习过程大概是这样的:老鼠的神经网络先做出转向的决定(朝左还是朝右),再观察它的环境.如果观察结果 是消极的,为了在下次做出不同的决定,网络会调整内部权重
神经网络在软件领域的几种应用场景
模式识别 具体的应用实例有面部识别,光学字符识别等
时序预测 神经网络可以用来进行数据预测.比如,明天的股票是涨是跌,明天是晴天还是雨天?
信号处理 人工耳蜗植入术和助听器需要过滤掉不必要的噪声并放大重要声音.神经网络可以经训练从而处理音频信号,并适当地过滤信号
控制 你可能听过自动驾驶汽车的研究动向.神经网络通常被用来管理物理汽车(或模拟汽车)的转向决策
软传感器 软传感器指的是测量集合的分析处理.温度计可以告诉你空气温度,其他传感器会告诉你湿度,气压,露点温度,空气质量,空气密度等数据,神经网络处理从这些传感器接收的输入数据,将这些数据作为整体进行评估
异常检测 由于神经网络擅于识别模式,他们还可以检测某些事情是否合乎规律.想象某个神经网络正在监视你的日常行为,经过一段时间,它已经掌握了你的行为模式.当你做错某些事时,它能做出提醒.
10.2 感知器
感知器是由就职于Cornell航空实验室的Frank Rosenblatt于1957年发明的,它可以被视为最简单的神经网络:单神经元计算模型.一个感知器由一个或多个输入,一个处理器和单个输出构成
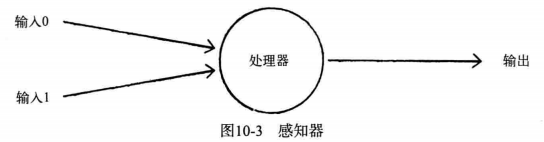
感知器算法
1.对每个输入,将它乘以对应的权重
2.对加权后的输入求和
3.把总和传入一个激励函数(activation function),得到感知器的输出
10.3 用感知器进行简单的模式识别
10.4 实现感知器
监督式学习方法
1.向感知器提供输入,这些输入的答案是已知的
2.让感知器猜测答案
3.计算误差.(感知器是否猜到了正确答案?)
4.根据误差调整所有权重
5.回到步骤(1)重复
感知器的误差可以被定义为正确答案和猜测之间的偏差
误差 = 正确输出 - 猜测输出
误差是权重调整的决定因素.权重的调整幅度通常用Δ权重表示
新权重 = 权重 + Δ权重
Δ权重可由误差和输入的乘积计算得到
Δ权重 = 误差 x 输入
因此:
新权重 = 权重 + 误差 x 输入
神经网络使用"学习常数",学习常数越大,权重的变化幅度也越大,这会让我们更快地解决问题.但如果权重变化幅度太大,我们可能会错过最优权重.反过来,学习常数越小,权重变化越慢,学习过程要花费的时间更多,权重调整幅度也越小,因此能提高神经网络的整体j精度
新权重 = 权重 + 误差 x 输入 x 学习常数

Trainer[] training = ];
Perceptron ptron;
;
;
;
;
;
float f(float x) {
;
}
void setup() {
size(,);
ptron = ,0.00001);
; i < training.length; i++) {
float x = random(xmin,xmax);
float y = random(ymin,ymax);
;
if(y < f(x)) {
answer = -;
}
training[i] = new Trainer(x,y,answer);
}
}
void draw() {
background();
translate(width / ,height / );
// 轴
strokeWeight();
stroke();
line(-,,,);
line(,-,,);
// 画出正确答案的线
strokeWeight();
stroke();
float x1 = xmin;
float y1 = f(x1);
float x2 = xmax;
float y2 = f(x2);
line(x1,y1,x2,y2);
stroke();
strokeWeight();
float[] weights = ptron.getWeights();
x1 = xmin;
y1 = (-weights[] - weights[] * x1) / weights[];
x2 = xmax;
y2 = (-weights[] - weights[] * x2) / weights[];
line(x1,y1,x2,y2);
ptron.train(training[count].inputs,training[count].answer);
count = (count + ) % training.length;
; i < count; i++) {
stroke();
strokeWeight();
fill();
int guess = ptron.feedforward(training[i].inputs);
) {
noFill();
}
ellipse(training[i].inputs[],training[i].inputs[],,);
}
}
// 老师
class Trainer {
float[] inputs;
int answer;
Trainer(float x,float y,int a) {
inputs = ];
inputs[] = x;
inputs[] = y;
inputs[] = ;
answer = a;
}
}
// 感知器
class Perceptron {
// 权重
float[] weights;
// 学习常数
float c;
Perceptron(int n,float c_) {
weights = new float[n];
; i < weights.length; i++) {
weights[i] = random(-,);
}
c = c_;
}
// 训练
// 1. inputs 输入 desired 已知答案
void train(float[] inputs,int desired) {
// 2. 根据输入做出猜测
int guess = feedforward(inputs);
// 3. 计算误差
float error = desired - guess;
// 4. 根据误差和学习常数调整权重
; i < weights.length; i++) {
weights[i] += c * error * inputs[i];
}
}
// 前馈
int feedforward(float[] inputs) {
;
; i < weights.length; i++) {
sum += inputs[i] * weights[i];
}
return activate(sum);
}
// 激励函数
int activate(float sum) {
) {
;
} else {
;
}
}
float[] getWeights() {
return weights;
}
}
10.5 转向感知器
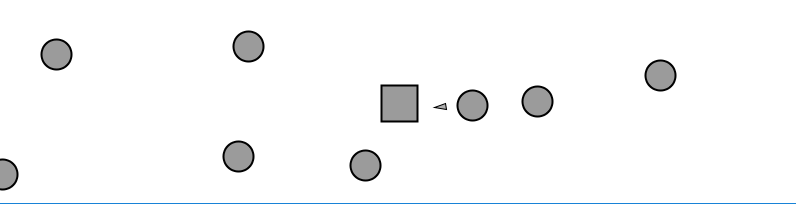
Vehicle v;
PVector desired;
ArrayList<PVector> targets;
void setup() {
size(, );
smooth();
desired = ,height/);
makeTargets();
v = new Vehicle(targets.size(), random(width), random(height));
}
void makeTargets() {
targets = new ArrayList<PVector>();
; i < ; i++) {
targets.add(new PVector(random(width), random(height)));
}
}
void draw() {
background();
rectMode(CENTER);
stroke();
strokeWeight();
fill(, );
rect(desired.x, desired.y, , );
for (PVector target : targets) {
fill(, );
stroke();
strokeWeight();
ellipse(target.x, target.y, , );
}
v.steer(targets);
v.update();
v.display();
}
void mousePressed() {
makeTargets();
}
class Vehicle {
Perceptron brain;
PVector location;
PVector velocity;
PVector acceleration;
float r;
float maxforce;
float maxspeed;
Vehicle(int n, float x, float y) {
brain = new Perceptron(n,0.001);
acceleration = ,);
velocity = ,);
location = new PVector(x,y);
r = 3.0;
maxspeed = ;
maxforce = 0.1;
}
void update() {
velocity.add(acceleration);
velocity.limit(maxspeed);
location.add(velocity);
acceleration.mult();
location.x = constrain(location.x,,width);
location.y = constrain(location.y,,height);
}
void applyForce(PVector force) {
acceleration.add(force);
}
void steer(ArrayList<PVector> targets) {
PVector[] forces = new PVector[targets.size()];
; i < forces.length; i++) {
forces[i] = seek(targets.get(i));
}
PVector result = brain.feedforward(forces);
applyForce(result);
PVector error = desired.get();
error.sub(location);
brain.train(forces,error);
}
PVector seek(PVector target) {
PVector desired = target.get();
desired.sub(location);
desired.normalize();
desired.mult(maxspeed);
PVector steer = desired.get();
steer.sub(velocity);
steer.limit(maxforce);
return steer;
}
void display() {
;
fill();
stroke();
strokeWeight();
pushMatrix();
translate(location.x,location.y);
rotate(theta);
beginShape();
vertex(, -r*);
vertex(-r, r*);
vertex(r, r*);
endShape(CLOSE);
popMatrix();
}
}
class Perceptron {
float[] weights;
float c;
Perceptron(int n, float c_) {
weights = new float[n];
c = c_;
; i < weights.length; i++) {
weights[i] = random(, );
}
}
void train(PVector[] forces, PVector error) {
; i < weights.length; i++) {
weights[i] += c*error.x*forces[i].x;
weights[i] += c*error.y*forces[i].y;
weights[i] = constrain(weights[i], , );
}
}
PVector feedforward(PVector[] forces) {
PVector sum = new PVector();
; i < weights.length; i++) {
forces[i].mult(weights[i]);
sum.add(forces[i]);
}
return sum;
}
}
class PVector {
float x;
float y;
PVector() {
x = ;
y = ;
}
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
float dot(PVector v) {
return x * v.x + y * v.y;
}
float angleBetween(PVector v2) {
float dot = this.dot(v2);
float theta = (float)Math.acos(dot / (this.mag() * v2.mag()));
return theta;
}
float dist(PVector v) {
PVector dist = this.get();
dist.sub(v);
return dist.mag();
}
}
10.6 还记得这是个"网络"吗
10.7 神经网络图
Network network;
void setup() {
size(, );
smooth();
network = ,height/);
Neuron a = ,);
Neuron b = ,);
Neuron c = ,-);
Neuron d = ,);
network.connect(a,b);
network.connect(a,c);
network.connect(b,d);
network.connect(c,d);
network.addNeuron(a);
network.addNeuron(b);
network.addNeuron(c);
network.addNeuron(d);
}
void draw() {
background();
// Draw the Network
network.display();
noLoop();
}
class Network {
ArrayList<Neuron> neurons;
PVector location;
Network(float x, float y) {
location = new PVector(x,y);
neurons = new ArrayList<Neuron>();
}
void addNeuron(Neuron n) {
neurons.add(n);
}
void connect(Neuron a, Neuron b) {
Connection c = ));
a.addConnection(c);
}
void display() {
pushMatrix();
translate(location.x, location.y);
for (Neuron n : neurons) {
n.display();
}
popMatrix();
}
}
class Connection {
Neuron a;
Neuron b;
float weight;
Connection(Neuron from, Neuron to,float w) {
weight = w;
a = from;
b = to;
}
void display() {
stroke();
strokeWeight(weight*);
line(a.location.x, a.location.y, b.location.x, b.location.y);
}
}
class Neuron {
PVector location;
ArrayList<Connection> connections;
Neuron(float x, float y) {
location = new PVector(x, y);
connections = new ArrayList<Connection>();
}
void addConnection(Connection c) {
connections.add(c);
}
void display() {
stroke();
strokeWeight();
fill();
ellipse(location.x, location.y, , );
for (Connection c : connections) {
c.display();
}
}
}
class PVector {
float x;
float y;
PVector() {
x = ;
y = ;
}
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
float dot(PVector v) {
return x * v.x + y * v.y;
}
float angleBetween(PVector v2) {
float dot = this.dot(v2);
float theta = (float)Math.acos(dot / (this.mag() * v2.mag()));
return theta;
}
float dist(PVector v) {
PVector dist = this.get();
dist.sub(v);
return dist.mag();
}
}
10.8 实现前馈动画

Network network;
void setup() {
size(, );
smooth();
// Create the Network object
network = , height/);
// Create a bunch of Neurons
Neuron a = , );
Neuron b = , );
Neuron c = , );
Neuron d = , -);
Neuron e = , );
Neuron f = , );
// Connect them
network.connect(a, b,);
network.connect(b, c,random());
network.connect(b, d,random());
network.connect(c, e,random());
network.connect(d, e,random());
network.connect(e, f,);
// Add them to the Network
network.addNeuron(a);
network.addNeuron(b);
network.addNeuron(c);
network.addNeuron(d);
network.addNeuron(e);
network.addNeuron(f);
}
void draw() {
background();
// Update and display the Network
network.update();
network.display();
// Every 30 frames feed in an input
== ) {
network.feedforward(random());
}
}
class Connection {
Neuron a;
Neuron b;
float weight;
boolean sending = false;
PVector sender;
;
Connection(Neuron from, Neuron to, float w) {
weight = w;
a = from;
b = to;
}
void feedforward(float val) {
output = val*weight;
sender = a.location.get();
sending = true;
}
void update() {
if (sending) {
sender.x = lerp(sender.x, b.location.x, 0.1);
sender.y = lerp(sender.y, b.location.y, 0.1);
float d = sender.get().dist(b.location);
) {
b.feedforward(output);
sending = false;
}
}
}
void display() {
stroke();
strokeWeight(+weight*);
line(a.location.x, a.location.y, b.location.x, b.location.y);
if (sending) {
fill();
strokeWeight();
ellipse(sender.x, sender.y, , );
}
}
}
class Network {
ArrayList<Neuron> neurons;
ArrayList<Connection> connections;
PVector location;
Network(float x, float y) {
location = new PVector(x, y);
neurons = new ArrayList<Neuron>();
connections = new ArrayList<Connection>();
}
void addNeuron(Neuron n) {
neurons.add(n);
}
void connect(Neuron a, Neuron b, float weight) {
Connection c = new Connection(a, b, weight);
a.addConnection(c);
connections.add(c);
}
void feedforward(float input) {
Neuron start = neurons.);
start.feedforward(input);
}
void update() {
for (Connection c : connections) {
c.update();
}
}
void display() {
pushMatrix();
translate(location.x, location.y);
for (Neuron n : neurons) {
n.display();
}
for (Connection c : connections) {
c.display();
}
popMatrix();
}
}
class Neuron {
PVector location;
ArrayList<Connection> connections;
;
;
Neuron(float x, float y) {
location = new PVector(x, y);
connections = new ArrayList<Connection>();
}
// Add a Connection
void addConnection(Connection c) {
connections.add(c);
}
void feedforward(float input) {
sum += input;
) {
fire();
sum = ;
}
}
void fire() {
r = ;
for (Connection c : connections) {
c.feedforward(sum);
}
}
void display() {
stroke();
strokeWeight();
,,,);
fill(b);
ellipse(location.x, location.y, r, r);
r = lerp(r,,0.1);
}
}
class PVector {
float x;
float y;
PVector() {
x = ;
y = ;
}
PVector(float x_,float y_) {
x = x_;
y = y_;
}
PVector get() {
PVector newVector = new PVector(x,y);
return newVector;
}
void add(PVector v) {
x = x + v.x;
y = y + v.y;
}
void sub(PVector v) {
x = x - v.x;
y = y - v.y;
}
void mult(float n) {
x = x * n;
y = y * n;
}
void div(float n) {
x = x / n;
y = y / n;
}
float mag() {
return sqrt(x * x + y * y);
}
void normalize() {
float m = mag();
) {
div(m);
}
}
void limit(float max) {
if(mag() > max) {
normalize();
mult(max);
}
}
float heading2D() {
return atan2(y,x);
}
float dot(PVector v) {
return x * v.x + y * v.y;
}
float angleBetween(PVector v2) {
float dot = this.dot(v2);
float theta = (float)Math.acos(dot / (this.mag() * v2.mag()));
return theta;
}
float dist(PVector v) {
PVector dist = this.get();
dist.sub(v);
return dist.mag();
}
}
10.9 结语
参考文献
Texturing and Modeling,Third Edition:A Procedural Approach
Alexander,R.McNeill. [Principles of Animal Locomotion] (http://t.co/IQ0iranE).Princeton,NJ:Princeton University Press,2002
Bentley,Peter. [Evolutionary Design by Computers] (http://t.co/XIp7b1zw).San Francisco:Morgan Kaufmann Publishers,1999.
Bohnacker,Hartmut,Benedikt Gross,Julia Laub,and Claudius Lazzeroni. [Generative Design:Visualize,Program,and Create with Processing] (http://t.co/8yekmakL).New York:Princeton Architectural Press,2012.
Flake,Gary William. [The Computational Beauty of Nature:Computer Explorations of Fractals,Chaos,Complex Systems,and Adaptation] (http://t.co/KdbTo1ZX).Cambridge,MA:MIT Press,1998
Hale,Nathan Cabot.[Abstraction in Art and Nature] (http://t.co/ztbQ1zCL).New York:Dover,1993.
Hildebrandt,Stefan,and Anthony J.Tromba. [Mathematics and Optimal Form] (http://t.co/IQ0iranE).New York:Scientific American Library,1985.Distributed by W.H.Freeman.
Kline,Morris. [Mathematics and the Physical World] (http://t.co/v84SZnGx).New York:Crowell,[1959]
Kodicek,Danny. [Mathematics and Physics for Programmers] (http://t.co/ygDdHMak).Hingham,MA:Charles River Media,2005.
McMahon,Thomas A.,and John Tyler Bonner. [On Size and Life] (http://t.co/EhX3KwZB).New York:Scientific American Library,1983.Distributed by W.H.Freeman
Mandelbrot.Benoit B. [The Fractal Geometry of Nature] (http://t.co/jHRQ5sQC).San Francisco:W.H.Freeman,1982
Pearce,Peter. [Structure in Nature Is a Strategy for Design] (http://t.co/zaGQMOMc).Cambridge,MA:MIT Press,1980.
Prusinkiewicz,Przemyslaw,and Aristid Lindenmayer. [The Algorithmic Beauty of Plants] (http://t.co/koD7FhJQ).New York:Springer-Verlag,1990.
Reas,Casey,and Chandler McWilliams.[Form+Code in Deisgn,Art,and Architecture] (http://t.co/1jGgwhvU).Design Briefs.New York:Princeton Architectural Press,2010.
Reas,Casey,and Ben Fry. [Processing:A Programming Handbook for Visual Designers and Artists] (http://t.co/dtODdOQp).Cambridge,MA:MIT Press,2007.
Thompson,D'Arcy Wentworth. [On Growth and Form:The Complete Revised Edition] (http://t.co/vncWa1uW).New York:Dover,1992.
Vogel.,Steven. [Life in Moving Fluids] (http://t.co/fyTbVta1).Princeton,NJ:Princeton University Press,1994.
Wade,David.Li: [Dynamic Form in Nature] (http://t.co/1QYDlsDH). Wooden Books.New York:Wlaker&Co.,2003.
Waterman,Talbot H. [Animal Navigation] (http://t.co/c2otv8LZ). New York:Scientific American Library,1989.Distributed by W.H.Freeman
Whyte,Lancelot Law. [Aspects of Form: A Symposium on Form in Nature and Art] (http://t.co/f7UkVLQM). Midland Books, MB 31.Bloomington: Indiana University Press,1966.
代码本色 用编程模拟自然系统 (Daniel Shiffman 著)的更多相关文章
- 使用PHP Socket 编程模拟Http post和get请求
这里给大家分享一段使用PHP Socket 编程模拟Http post和get请求的代码,非常的实用,结尾部分我们再讨论下php模拟http请求的几种方法. <?php /** * 使用PHP ...
- Windows下编程--模拟时钟的实现
windows下编程--模拟时钟的实现: 主要可以分为几个步骤: (1) 编写按键事件处理(启动和停止时钟) (2) 编写时钟事件处理,调用显示时钟函数 (3) 编写显示时钟函数,要调用显 ...
- 编写Java程序,用套接字编程模拟实现银行认证过程
需求说明: 某银行一核心服务器部署了一个资金交易来往的系统,为了防止黑客入侵窃取数据,该银行专门开发了一款负责安全认证的智能机器人守护服务器,对外来访问做多重身份认证.现在要求你用套接字编程模拟实现这 ...
- [.NET] 怎样使用 async & await 一步步将同步代码转换为异步编程
怎样使用 async & await 一步步将同步代码转换为异步编程 [博主]反骨仔 [出处]http://www.cnblogs.com/liqingwen/p/6079707.html ...
- socket编程模拟linux下的ssh代码实现
实现思路: 1.提供输入指令的客户端: 2.提供返回执行指令结果的服务端 3.寻找服务端返回结果一次无法全部接收的解决思路 服务端代码(ssh_server.py) #coding=utf-8 imp ...
- java 网络编程 模拟browser
--java模拟实现browser,主要代码: package socket; import java.io.*; import java.net.*; public class MyHttpClie ...
- python 反人类函数式编程模拟while和if控制流
比如下面这个简单明了的命令式程序,它不断捕捉用户输入的内容,然后对其求和.直到用户输入一个以'0'开头的字符串,停止捕捉. while 1: line = input() ': print(sum(m ...
- Java使用HTTP编程模拟多参数多文件表单信息的请求与处理
本文目的是提供Java环境下模拟浏览器页面提交多参数多文件表单请求以及解析请求的Demo代码.这里用Java提供的HttpURLConnection类做HTTP请求,再原始点可以直接使用socket. ...
- unity代码创建草和模拟风的效果
void Start() { Test4(); } //草 private Vector3[] grassArray = new Vector3[7]; private GameObject gras ...
随机推荐
- npm 升降级
npm 降级 $ npm -v 6.4.1 $ sudo npm install npm@4 -g /usr/bin/npm -> /usr/lib/node_modules/npm/bin/n ...
- dom常用操作
创建节点:document.createElement(元素名), document.createTextNode(文本内容) 添加节点:parent.appendChild(newChild) 移除 ...
- HDU - 1575——矩阵快速幂问题
HDU - 1575 题目: A为一个方阵,则Tr A表示A的迹(就是主对角线上各项的和),现要求Tr(A^k)%9973. Input数据的第一行是一个T,表示有T组数据. 每组数据的第一行有n( ...
- 基于FastJson的通用泛型解决方案
由于项目使用的是fastjson,也无法换成其他的序列化框架,所以研究了一下他对泛型序列化和反序列化的支持能力,最终解决了这个问题. 要达成的目标 我的封装方式属于通用封装,我要达到的目标是如下的使用 ...
- Mac系统下安装PyCharm
首先,进入 PyCharm 的官网,https://www.jetbrains.com/pycharm/ 有macOS.Windows.Linux三个系统的自由选择,这里我们选macOS,然后down ...
- Json 网络传递解析异常
在项目中碰到一个bug,A项目请求B项目,获取到的Json无法解析,B项目封装的Json,在项目内部可以正常解析,问题并不是Json 解析的错误,而是实体Bean中有数组类型的字段;解决办法就是对封装 ...
- Shell 与正则表达式part1
1.什么是shell? shell代表两个层面的意思,一个是命令解释器,比如:BASH,另外一个是shell脚本(利用shell的功能所写的一个程序,这个程序是使用纯文本文件,将一些shell的语法与 ...
- day71 菜单的排序 点击被选中
菜单的排序:(给菜单设置权重,权重高的让他显示在上面) from django import template from django.conf import settings from collec ...
- [Leetcode 144]二叉树前序遍历Binary Tree Preorder Traversal
[题目] Given a binary tree, return the preordertraversal of its nodes' values. Example: Input: [1,null ...
- 1093 字符串A+B
给定两个字符串 A 和 B,本题要求你输出 A+B,即两个字符串的并集.要求先输出 A,再输出 B,但重复的字符必须被剔除. 输入格式: 输入在两行中分别给出 A 和 B,均为长度不超过 106 ...
