【ACM】棋盘覆盖 - 大数除

棋盘覆盖

时间限制：3000 ms  |  内存限制：65535 KB

难度：3

 

描述

在一个2^k×2^k（1<=k<=100）的棋盘中恰有一方格被覆盖，如图1（k=2时），现用一缺角的2×2方格（图2为其中缺右下角的一个），去覆盖2^k×2^k未被覆盖过的方格，求需要类似图2方格总的个数s。如k=1时，s=1;k=2时，s=5

 

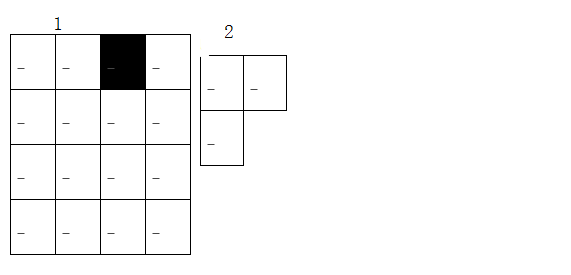
输入

第一行m表示有m组测试数据；
每一组测试数据的第一行有一个整数数k;

输出

输出所需个数s;

样例输入

3
1
2
3

样例输出

1
5
21

思路：类似大数乘进行处理

#include <iostream>
#include <cstdio>
#include <cmath>

using namespace std;

int main(){
    int a[];
    int n;
    cin>>n;
    while (n--)
    {
        int m;
        cin>>m;
        int sum = ;
        int temp;
        int k = ;
        a[] = ;
        for (int i =  ; i < m ; i++)
        {
            for (int j =  ; j < k; j++)
            {
                temp = a[j] *  + sum;
                a[j] = temp % ;
                sum = temp / ;
            }
            while (sum > )
            {
                a[k++] = sum % ;
                sum /= ;
            }
        }
        a[] -= ;
        int d = k-;
        int high = a[d]/>?d:d-;
        sum = ;
        while (d >= )
        {
            temp = a[d] + sum;
            if (temp / > )
            {
                a[d] = temp / ;
                sum = (temp-a[d]*)*;
                d--;
            }
            else
            {
                sum = a[d]*;
                a[d] = ;
                d--;
            }

        }

        for (int z = high ; z>=; z--)
        {
            cout<<a[z];
        }
        cout<<endl;
    }

    return ;
}