Spring Cloud学习笔记之微服务架构

什么是微服务
架构优点
架构的挑战
设计原则

什么是微服务

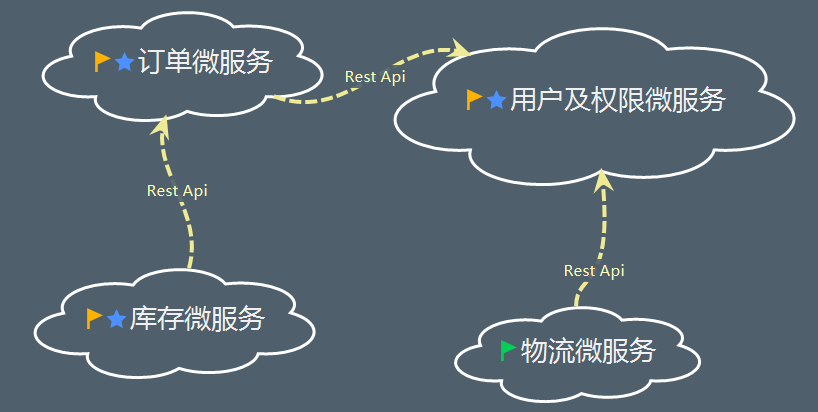
    微服务构架方法是以开发一种小型服务的方式，来开发一个独立的应用系统的。
    其中每个小型服务都运行在自己的进程中，并经常采用HTTP资源API这样轻量的机制来相互通信。
    这些服务围绕业务功能进行构建，并能通过全自动的部署机制来进行独立部署。
    这些微服务可以使用不同的语言来编写，并且可以使用不同的数据存储技术。
    对这些微服务我们仅做最低限度的集中管理。

架构优点

1. 易于开发和维护

一个微服务只关注一个特定的业务功能。所以它的业务清晰，代码量较少。开发和维护单个微服务相对是比较简单的，而整个应用是由若干个微服务构建而成的，所以整个应用也会维持在可控状态。

2. 单个微服务启动较快

单个微服务代码量较少，所以启动会比较快

3. 局部修改容易部署

单体应用只要有修改，就得重新部署整个应用，微服务解决了这样的问题。一般来讲，对某个微服务进行修改，只需要部署这个服务即可。

4. 技术栈不受限

在微服务中，我们可以结合项目业务及团队的特点，合理选择技术栈。例如某些服务可使用关系型数据库，某些应用有图形计算的需求，可以使用Neo4j,某些应用服务有并发需求，可以采用内存数据库(redis、couchbase);甚至可以根据需要，部分微服务使用JAVA开发，部分微服务使用NodeJS进行开发。

5. 按需伸缩

我们可以根据需求，实践细粒度的扩展。例如，系统中某个微服务遇到了瓶颈。我们可以结合这个微服务的业务特点，增加内存，升级CPU或者增加节点。

架构的挑战

1. 运维要求较高

更多的服务意味着更多的运维投入。在单体架构中，只需要保证一个应用的正常运行；而在微服务中，需要保证几十个乃至几百个服务的正常运行与协作。

2. 分布式固有的复杂性

使用微服务构建的是分布式系统。对于一个分布式系统，系统容错、网络延迟、分布式事务等都给我们带来了很大的挑战。

3. 接口调整成本高

微服务之间通过接口进行通信。如果修改某一个微服务的API。可能所有使用了该接口的微服务都需要做调整。

4. 重复劳动

很多服务可能都会使用到相同的功能。再这个功能并没有达到分解为一个微服务的程序，这个时候，可能各个服务都会开发这一功能，从而导致代码重复。

设计原则

微服务有优点，也有缺点，我们需要避重就轻,所以在实践中，需要遵守一些原则。

1. 单一职责原则

高内聚，低耦合
遵守单一职责原则，将不同的职责封装到不同的类或模块中

2. 服务自治原则

每个服务应当具备独立的业务能力，依赖与运行环境

3. 轻量级通信原则

4. 接口明确原则

每个服务的对外接口应该明确定义，并尽量保持不变

Spring Cloud: http://projects.spring.io/spring-cloud/

GitHub: https://github.com/spring-cloud/