機器學習基石 机器学习基石（Machine Learning Foundations） 作业2 第10题 解答

由于前面分享的几篇博客已经把其他题的解决方法给出了链接，而这道题并没有，于是这里分享一下：

原题：

这题说白了就是求一个二维平面上的数据用决策树来分开，这就是说平面上的点只能画横竖两个线就要把所有的点SATTER掉，先给出四个点的情况，如下：

第一种分割方式：

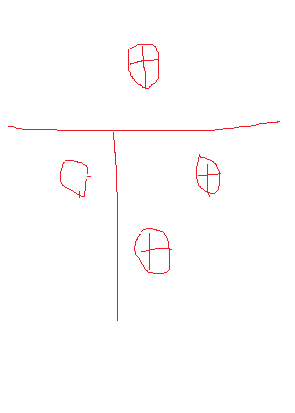
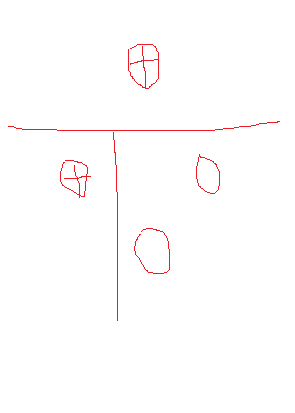
第二种分割方式

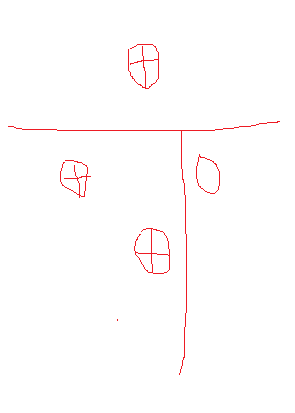
第三种分割方式   为第一种的  上下导致。

第四种分割方式   为第二种的  上下导致。

第 5 6 7 8 分别为  第1 2 3 4 种中正负点的互换，

以此方式，我们可以画出  16种，这里不全部给出了。

由此可以看出4个点的时候被satter掉。

这时候我们加入第5个点，用黑色表示，如下：

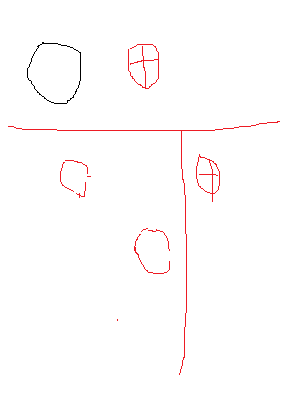
由于 维度D=2,也就是说我们只能画两笔，一个横一个竖。这时候我们以上面的那个图为例子，我们可以发现，如果上面的竖线固定下面的那个竖线可以自由移动，这时候下面的这三个点可以satter掉，但是上面的那两个点是无法satter掉的，由这个例子我们发现D=2的时候它的VC为4，也就是2**D, 这个方法是试错法子，不过也算是有了些解释。

也就是说选项中只有第一个满足，于是选这个。