OI网络流简单学习笔记

持续更新！

基本上只是整理了一下框架，具体的学习给出了个人认为比较好的博客的链接。

。。怎么说呢，最基础的模板我就我不说了吧qwq，具体可以参考一下这位大佬写的博客：最大流，最小割，费用流

费用流

跑最大费用流的时候可以把边权都变成负的，然后按照原先的方法跑最小费用流即可。
每个点只能经过一次的时候，就拆点，然后两个点之间连容量为1费用为0的边。连路径的时候，强制从v'向u连边。

经典费用流模型

连续M个元素最多选K个
给你N个元素，每个元素都有一个权值ai（可正可负），要求从中你选出一些，满足对于任意相邻的M个元素当中最多只有K个元素被选出，使得总权值最大。
BZOJ1283 序列

二分图

设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

判定二分图：黑白染色，如果有矛盾，就不是二分图。

如果进行到最后都没有矛盾，那就是二分图。
或者说，如果一个图里面没有奇环，就是二分图。

二分图最大匹配

就是一个二分图中最多能够匹配的对数。
建立一个源点S，一个汇点T，S点向左点集X连边，右点集Y向T点连边，两个点集间从左向右连边，容量都是1，求最大流即可。
很显然一个流就代表一个匹配
（求最大流的算法主要是KM（\(N*M^2\)），dinic算法（\(M*N^2\)）。dinic算法求二分图最大匹配的时间复杂度是\(M*\sqrt N\)）

二分图最大权匹配

别的和最大匹配一样，但是给X到Y的边加费用为对应的边权，然后求S到T的最大费用流（注意这里不是最大费用最大流，因为那个是要求在最大流基础上的最大费用，可能就不是全局最大费用了）

二分图最小点覆盖

就是选出来最少数量的点，使得这些点所连接的边的并集覆盖掉所有的边。
定理：最小点覆盖=最大匹配
证明：首先，对于flow个最大匹配，每个匹配都需要一个点，也就是最少需要flow个点。实际上最多也是只需要flow个点。一条边只需要一个点就可以了；选了flow个点后，还有一条边两端的点都不在这个点集中说明还可以增广，这就和最大流的假设违背了。
一般适用于：

两种选择，至少要选择一个，每个选择有代价的最优化问题（比如说BZOJ1741 asteroids )

二分图最小点权覆盖集

定理：最小点权覆盖=最小割=最大流
证明：S-X和Y-T的连对应点权容量的边， X-Y的连容量inf的边，然后求最小割，首先中间的边不会被割，也就是左右边的边选一些割掉（左右选一些点作为覆盖点）。
证明即是建图方式。

二分图最大独立集

在二分图中选出来一些点，使得这些点两两之间都没有边相连。
定理：最大独立集=点数-最小点覆盖
yy的证明：一条边只有两个点，如果排除这些最小点覆盖的集合，显然每条边只剩下剩下的那个点。这些点只有通过边才能与其他点相连，但是它们相连的边上的另外一点都已经被排除，所以相当于它们“与世隔绝”，所以这些点集就是最大独立集的数量。

二分图最大点权独立集

定理：总点权-最小割
yy的证明：正难则反，这个东西肯定是总点权减去一个什么值，然后这个值还要尽可能小，而且减去这个东西后还要保证留下来的点两两之间互不到达。将这个图断开的最小代价就是最小割了，所以自然减去的东西就是最小割（最小点权覆盖集）了qwqwq

小结：

二分图最大匹配=二分图最小点覆盖=最小割=最大流=n-最大独立集。

二分图最小权覆盖和二分图最大权独立集互补。

DAG最小路径覆盖（不相交）

什么是最小路径覆盖呢？就是选出若干个路径，使得这些路径的并经过所有的点。
把原图的每个点V拆成Vx和Vy两个点，如果有一条有向边A->B，那么就加边Ax−>By。这样就得到了一个二分图。那么(定理）最小路径覆盖=原图的结点数-新图的最大匹配数。
yy的证明：把原先的每一个点都看成一条路径，每连一条边就是等于将两个点合并起来，路径数量-1。
例题：BZOJ2150部落战争题解

DAG最小路径覆盖（可相交）

和上面的大概相同，先用floyd求出原图的传递闭包，即如果a到b有路径，那么就加边a->b。然后就转化成了最小不相交路径覆盖问题。
例题：POJ2594 题解

霍尔定理（hall定理）

二分图G中的两部分顶点组合成的集合分别为X,Y。G中有一组无公共点的边，一端恰好为组成X的点（完美匹配）的充分必要条件是：X中的任意K个点至少与Y中的K个点相邻。
对于X中的一个点集W，令\(N_G(W)\)为W的所有邻居，霍尔定理即对于任意W，\(|W|<=|N_G(W)|\)
证明：（来自wzd dalao的博客）

必要性证明
假如一个二分图G存在完美匹配，且不满足Hall定理。那么对于某k个点，它们连向的都不足k个点。那么它们是怎么都被匹配上的？？？很显然必要性正确。
充分性证明
假如一个二分图G不存在完美匹配，且满足Hall定理。那么假如有一种最大匹配的方案，既然不存在完美匹配，可以找到至少一个未被匹配的点。因为这个二分图满足Hall定理，所以这个点一定连向了至少一个点。假如这个点不在最大匹配中，它们就匹配了，怎么可能呢？？？那么这个点在最大匹配中！所以一定有一个点和它匹配了。因为这个二分图满足Hall定理，所以这个点又一定连向了除它匹配的点外的至少一个点。假如这个点不在最大匹配中，一条增广路找到了，怎么可能呢？？？那么这个点在最大匹配中！所以…… 看懂了吧！我们一定能推出矛盾！所以充分性正确。

霍尔定理（hall定理）拓展

对于X,Y二分图最大匹配数=\(|S|-max{|W|-|N(W)|}\)，其中S是X全集的个数，W是S的子集。
这个结论可以让我们不通过建图，就可以知道最大匹配数量。

最小割

最小割，图中所有的割中，边权值和最小的割为最小割。

最小割是解决利益冲突情况下的利益最大化问题

可能割边

就是有可能在最小割中的边。
定理：当且仅当该边满流且残余网络（包括反向边）中该边两端点处于不同SCC时，该边可能在最小割中。

关键割边

一定在最小割中的边。
将可能割边的容量加一，如果求得的最小割增大，证明该边一定是关键割边。

无向图最小割树。（分治最小割）

一些性质：
对于两个点(s,t)的最小割。这个最小割将将所有点分成左右两个集合X、Y。对于X中任意一点a与Y中任意一点b， (a,b)的最小割小于等于(s,t)的最小割。因此，每次递归计算分成的两个集合的最小割，更新答案。
也就是说明，每求一次最小割，都可以把一个大点集分成两个小点集，显然最后能分的次数是n-1次，也就是无向图不同的最小割最多n-1个。
例题：BZOJ2229/ZJOI2011 最小割题解

最大权闭合子图

什么是闭合子图：给定一个有向图，从中选择一些点组成一个点集V。对于V中任意一个点，其后续节点都仍然在V中。
入门的话建议大家先去看这篇博客戳我

定理：最大权闭合子图=总点权-最小割

最大权闭合子图建模方式：先把答案加上所有的正权值，然后从源点向所有的正权点连一条流量为权值的边，所有的负权值的点向汇点连一条流量为权值相反数的边。原图中的所有的限制关系(i,j)均建立一条从i到j的流量为inf的边，最终的答案减去这个图的最小割就可以了。

最大密度子图

和分数规划有关，蒟蒻还不会。。。。回来再补。

平面图与对偶图

参考来自这位dalao的博客，在此表示感谢！
什么是平面图？任意两边之间的交点只能是顶点。
什么是对偶图？设有平面图G=(V,E)，满足下列条件的图G'= (V',E') 称为图G的对偶图：G的任一面Ri内有且仅有一点Vi'；对G的域Ri和Rj的共同边界Ek，画一条边Ek'=(Vi',Vj')且只与Ek交于一点；若Ek完全处于Ri中，则Vi'有一自环Ek'。

之间的关系：平面图最小割=对偶图最短路

作用：用求最短路来代替最小割，降低时间复杂度。
图片示例：

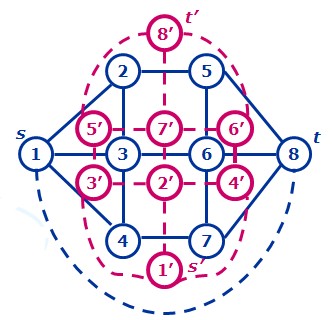
（蓝色的是平面图，紫色的是对偶图）
例题：NOI2010海拔题解戳我

混合图欧拉回路

发现已经有大佬写啦！那就贴上好了qwq 戳我

给出一个有向图, 问至少删掉多少条边使得这个图有欧拉回路

设pi=in[i]-out[i]。如果pi>0,从S连向i，否则i连向T，容量为|pi|.然后一条有向边(u,v),网络流中连(v,u,1,1)◦求最小费用最大流，一条流表示把中间的边都删掉了，满流就代表着把入度出度不平衡的点给平衡了。

有上下界的网络流