快速排序 java实现 (原理-优化) 三路快排
一、基本的快速排序
在数组中选取一个元素为基点,然后想办法把这个基点元素移动到它在排好序后的最终位置,使得新数组中在这个基点之前的元素都小于这个基点,而之后的元素都大于这个基点,然后再对前后两部分数组快速排序,直到数组排序完成。
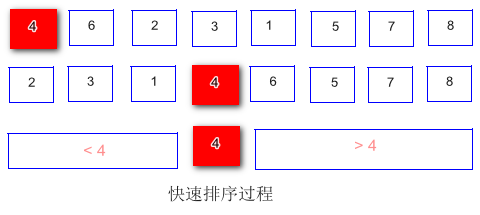
代码实现:
public void quickSorted ( int arr[] ) {
int n = arr.length - 1; // 闭区间 [0...n]
__quickSorted (arr, 0, n);
}
private __quickSorted( int arr[], int L, int R) {
if ( (L >= R) {
return;
}
// 将基点移动到最终位置的方法
int p = __partioner(arr, L, R);
// 递归拆分数组
__quickSorted(arr, L, p - 1);
__quickSorted(arr, p + 1, R);
}
那么最大的问题就是怎么把这个基点移动到它最终应该所在的位置。
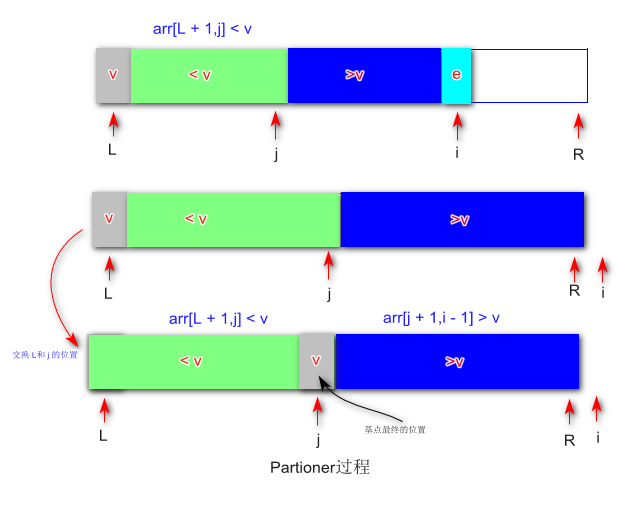
代码实现:
private int __partioner ( int arr[], int L, int R ) {
int v = arr[L];
// [L + 1, j] < v ; [j + 1, i) > v;
int j = L;
for ( int i = L + 1; i <= R; i++ ) {
if ( arr[i] < v) {
// 交换 arr[i] 和 arr [j + 1]
int tmp = arr[j + 1];
arr[j + 1] = arr[i];
arr[i] = tmp;
j++;
}
}
// 交换 arr[j] 和arr[L]
int tmp = arr[j];
arr[j] = arr[L];
arr[L] = tmp;
return j;
}
最终实现:
public void quickSorted ( int arr[] ) {
int n = arr.length - 1; // 闭区间 [0...n]
__quickSorted (arr, 0, n);
}
private __quickSorted( int arr[], int L, int R) {
if ( (L >= R) {
return;
}
// 将基点移动到最终位置的方法
int p = __partioner(arr, L, R);
// 递归拆分数组
__quickSorted(arr, L, p - 1);
__quickSorted(arr, p + 1, R);
}
private int __partioner ( int arr[], int L, int R ) {
int v = arr[L];
// [L + 1, j] < v ; [j + 1, i) > v;
int j = L;
for ( int i = L + 1; i <= R; i++ ) {
if ( arr[i] < v) {
// 交换 arr[i] 和 arr [j + 1]
int tmp = arr[j + 1];
arr[j + 1] = arr[i];
arr[i] = tmp;
j++;
}
}
// 交换 arr[j] 和arr[L]
int tmp = arr[j];
arr[j] = arr[L];
arr[L] = tmp;
return j;
}
快速排序完整代码
二、快速排序的优化
1. 快速排序的第一次优化,减小递归的深度,转而使用 选择排序
private __quickSorted( int arr[], int L, int R) {
// if ( (L >= R) {
// return;
// }
// 快速排序的第一次优化,减小递归的深度,转而使用 选择排序
if ( R - L <= 15) {
insertSorted(arr, L, R);
return;
}
// 将基点移动到最终位置的方法
int p = __partioner(arr, L, R);
// 递归拆分数组
__quickSorted(arr, L, p - 1);
__quickSorted(arr, p + 1, R);
}
// 减小递归的深度转而使用选择排序
private void insertSorted(int arr[], int L, int R) {
for (int i = L + 1; i <= R; i++) {
int i = arr[i];
int j;
for (j = i; j > L && arr[j - 1] > e; j--) {
arr[j] = arr[j - 1];
}
}
return;
}
2. 优化二,基点的选择随机化
private int __partioner ( int arr[], int L, int R ) {
// 第二次优化,将基点的选择随机化
int rand = (new Random().nextInt(R + 1)) + L;
// 交换最左侧和随机点的元素
int tmp = arr[rand];
arr[rand] = arr[L];
arr[L] = tmp;
int v = arr[L];
// [L + 1, j] < v ; [j + 1, i) > v;
int j = L;
for ( int i = L + 1; i <= R; i++ ) {
if ( arr[i] < v) {
// 交换 arr[i] 和 arr [j + 1]
int tmp = arr[j + 1];
arr[j + 1] = arr[i];
arr[i] = tmp;
j++;
}
}
// 交换 arr[j] 和arr[L]
int tmp = arr[j];
arr[j] = arr[L];
arr[L] = tmp;
return j;
}
三、两路快排
解决排序的数组中存在多数重复元素的情况
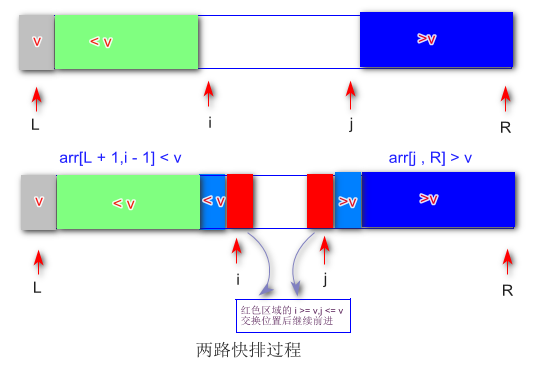
代码实现
public void quickSorted ( int arr[] ) {
int n = arr.length - 1; // 闭区间 [0...n]
__quickSorted (arr, 0, n);
}
private __quickSorted( int arr[], int L, int R) {
// if ( (L >= R) {
// return;
// }
// 快速排序的第一次优化,减小递归的深度,转而使用 选择排序
if ( R - L <= 15) {
insertSorted(arr, L, R);
return;
}
// 将基点移动到最终位置的方法
int p = __partioner(arr, L, R);
// 递归拆分数组
__quickSorted(arr, L, p - 1);
__quickSorted(arr, p + 1, R);
}
private int __partioner ( int arr[], int L, int R ) {
// 第二次优化,将基点的选择随机化
int rand = (new Random().nextInt(R + 1)) + L;
// 交换最左侧和随机点的元素
int tmp = arr[rand];
arr[rand] = arr[L];
arr[L] = tmp;
int v = arr[L];
// 两路快排的实现过程
int i = L + 1;
int j = R ;
while (true) {
while (i <= R && arr[i] < v ){
i++;
}
while (j >= L + 1 && arr[j] > v) {
j--;
}
if (i > j) {
break;
}
// 交换 i 和 j 的位置
int tmp arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
int tmp arr[L];
arr[L] = arr[j];
arr[j] = tmp;
return j;
}
// 减小递归的深度转而使用选择排序
private void insertSorted(int arr[], int L, int R) {
for (int i = L + 1; i <= R; i++) {
int i = arr[i];
int j;
for (j = i; j > L && arr[j - 1] > e; j--) {
arr[j] = arr[j - 1];
}
}
return;
}
两路快排代码实现
四、三路快排

代码实现:
public static void quickSorted3Ways(int arr[]) {
int n = arr.length -1;
// arr[0, n] 闭区间
__quickSorted3Ways(arr, 0, n);
}
private static void __quickSorted3Ways(int[] arr, int L, int R) {
// if (L >= R) {
// return;
// }
// 快速排序的第一次优化,减小递归的深度,转而使用 选择排序
if ( R - L <= 15) {
insertSorted(arr, L, R);
return;
}
// 第二次优化,将基点的选择随机化
int rand = (new Random().nextInt(R + 1)) + L;
// 交换最左侧和随机点的元素
int tmp = arr[rand];
arr[rand] = arr[L];
arr[L] = tmp;
int v = arr[L];
// partioner
// 这三个变量的初始值 , 相当重要
int lt = L; // arr[L + 1, lt] < v
int gt = R + 1; // arr[gt, R] > v
int i =L + 1; // arr[lt + 1, i ) ==v // 此处的 i 的比较对象
while (i < gt ) {
if (arr[i] < v) {
SortedHandler.swap(arr, i, lt + 1);
lt++;
i++;
} else if (arr[i] > v) {
SortedHandler.swap(arr, i, gt - 1);
gt--;
} else {
i++;
}
}
SortedHandler.swap(arr, lt, L);
__quickSorted3Ways(arr, L, lt -1);
__quickSorted3Ways(arr, gt, R);
}
三路快排
最后附上整篇 关于快速排序从实现到逐步优化的思路图 (画到我怀疑人生了....)
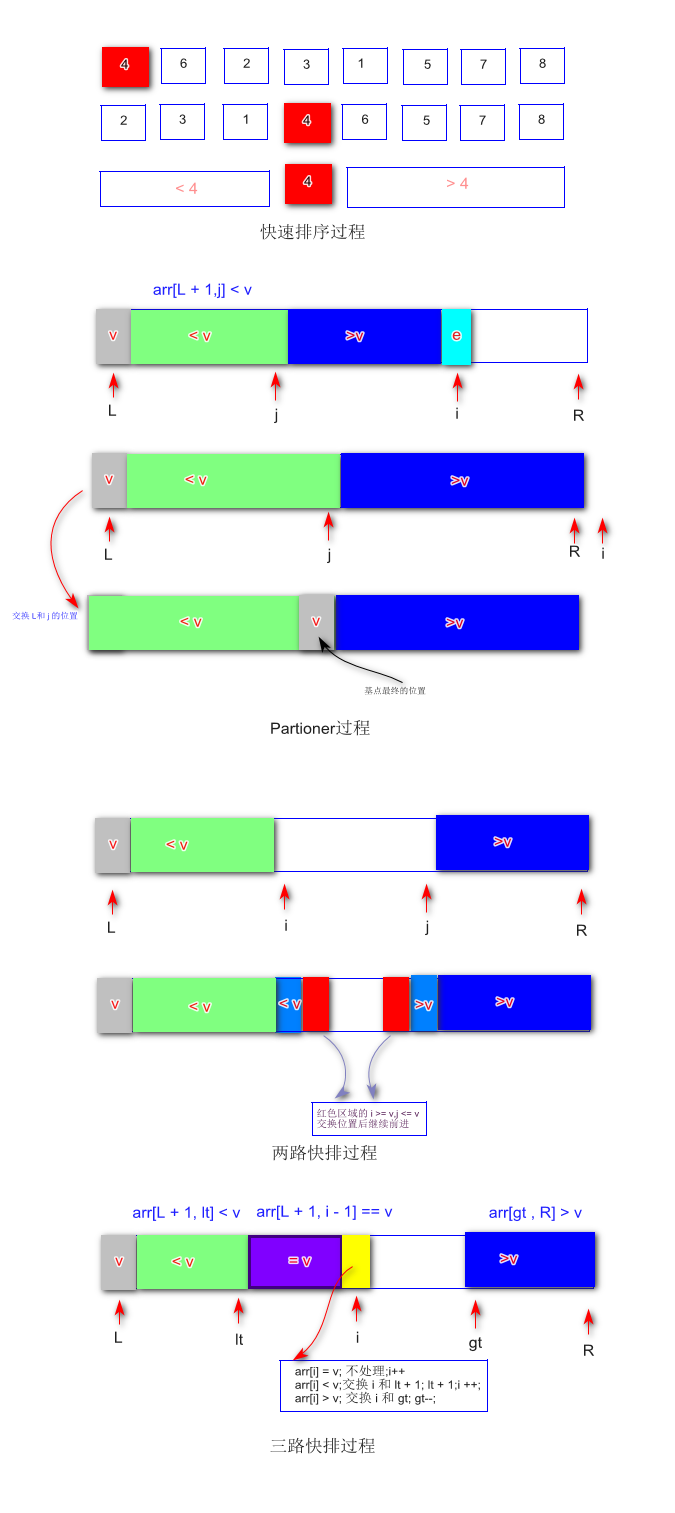
快速排序 java实现 (原理-优化) 三路快排的更多相关文章
- 快速排序—三路快排 vs 双基准
快速排序被公认为是本世纪最重要的算法之一,这已经不是什么新闻了.对很多语言来说是实际系统排序,包括在Java中的Arrays.sort. 那么快速排序有什么新进展呢? 好吧,就像我刚才提到的那样(Ja ...
- LeetCode 75. Sort Colors (颜色分类):三路快排
Given an array with n objects colored red, white or blue, sort them in-place so that objects of the ...
- 普林斯顿大学算法课 Algorithm Part I Week 3 重复元素排序 - 三路快排 Duplicate Keys
很多时候排序是为了对数据进行归类,这种排序重复值特别多 通过年龄统计人口 删除邮件列表里的重复邮件 通过大学对求职者进行排序 若使用普通的快排对重复数据进行排序,会造成N^2复杂度,但是归并排序和三路 ...
- leetcode 75 Sort Colors 计数排序,三路快排
解法一:计数排序:统计0,1,2 的个数 时间复杂度:O(n) 空间复杂度:O(k) k为元素的取值范围, 此题为O(1) class Solution { public: void sortC ...
- LeetCode 75. Sort Colors (python一次遍历,模拟三路快排)
LeetCode 75. Sort Colors (python一次遍历,模拟三路快排) 题目分析: 本题需要实现数字只包含0,1,2的排序,并且要求一次遍历. 由于只用把数字隔离开,很容易想到快排的 ...
- 【C语言编程入门笔记】排序算法之快速排序,一文轻松掌握快排!
排序算法一直是c语言重点,各个算法适应不用的环境,同时,在面试时,排序算法也是经常被问到的.今天我们介绍下快速排序,简称就是快排. 1.快速排序思想: 快排使用 分治法 (Divide and con ...
- Java写 插入 选择 冒泡 快排
/** * Created by wushuang on 2014/11/19. */ public class SortTest { @Test public void mainTest() { i ...
- <泛> 多路快排
今天写一个多路快排函数模板,与STL容器兼容的. 我们默认为升序排序 因为,STL容器均为逾尾容器,所以我们这里采用的参数也是逾尾的参数 一.二路快排 基本思路 给你一个序列,先选择一个数作为基数,我 ...
- LeetCode75----分类颜色(变相快排)
给定一个包含红色.白色和蓝色,一共 n 个元素的数组,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色.白色.蓝色顺序排列. 此题中,我们使用整数 0. 1 和 2 分别表示红色.白色和蓝色. ...
随机推荐
- mac os、linux及unix之间的关系
unix 是由贝尔实验室开发的多用户.多任务操作系统 linux是一类Unix操作系统的统称,严格来说,linux系统只有内核叫“linux”,而linux也只是表示其内核,但因为习惯使然,人们 习惯 ...
- Core1.1环境下,自己实现的一个简单的CRUD框架(反射实现)
我实现了一个简单的EF框架,主要用于操纵数据库.实现了对数据库的基本操纵--CRUD 这是项目结构 这是一个 core 下的 DLL 写了一个数据库工厂,用于执行sql语句.调用sql语句工厂 写了一 ...
- iOS学习之UITableView中Cell的操作
接着iOS学习之Table View的简单使用 这篇,这里主要讲UITableView 中的Cell的操作,包括标记.移动.删除.插入. 为了简单快捷,直接从原来那篇的代码开始,代码下载地址:http ...
- JAVA中List的几个方法
add()方法.插入某个位置的数据,他有两个参数一个参数是下标,一个参数是元素.需要注意的是下标大小应该小于等于List集合大小,否则就会抛出下标越界异常! 代码: public static ...
- 五分钟带你入门TensorFlow
TensorFlow是Google开源的一款人工智能学习系统.为什么叫这个名字呢?Tensor的意思是张量,代表N维数组:Flow的意思是流,代表基于数据流图的计算.把N维数字从流图的一端流动到另一端 ...
- Java 代理机制
Table of Contents 1 引言 2 常见的代理 3 代理模式UML图 4 代理模式实例 5 java动态代理 5.1 java动态代理UML图 6 代理模式与装饰者模式的区别 6.1 装 ...
- ZPL语言说明文档
■格式命令(format commands) 以︿开始 用于设定标签格式与数据 多条格式指令按顺序执行 ■控制指令(control commands) 以~开始 迫使打印机立即执行某一个指令的操作 可 ...
- java 将一个数组中的值按逆序重新存放,例如,原来顺序为:9,5,7,4,8,要求改为:8,4,7, 5,9。
public class Test3 { public static void main(String[] args) { int[] grade = {87,88,89,98,78}; int m; ...
- [SoapUI] 设置Excel的第一行为自动过滤
import org.apache.poi.ss.util.* XSSFWorkbook workbook = new XSSFWorkbook() XSSFSheet sheet = workboo ...
- Win10系统SQL数据库安装
Win10系统MySQL数据库安装 1. 安装文件下载 下载地址: https://downloads.mysql.com/archives/community/ 下载版本: mysql-8.0.15 ...
