ACM International Collegiate Programming Contest World Finals 2013

A - Self-Assembly

题目描述：给出\(n\)个正方形组件，正方形每条边有一个标签，标签可能是00，表示这条边不能与其它边相拼，也可能是一个字母加正号或负号，相同字母不同符号的边可以相拼。每个组件有无限个，问利用这些组件是否能拼出一个无限大的多边形。

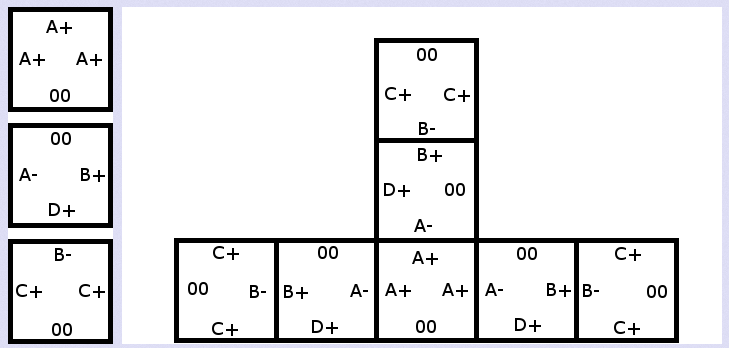
solution
拆点，每个正方形拆成\(4\)个点，每条边一个，然后每条边拆成两个点（出点和入点），然后新增\(52\)个点，表示\(52\)个标签，然后每个点拆成两个点（出点和入点）。连边，然后判断是否有环，如果有，则能拼出一个无限的多边形，否则不能。

时间复杂度：\(O(n*8+n*4*4)\)

C - Surely You Congest

题目描述：给出一个无向图，每个点上有一些车，这些车都要到\(1\)号点，车都走最短路径，但不能有两辆车同时同向进入某条边，但可以进入某个点，每辆车都同时出发。问最多有多少辆车能同时出发。

solution
先求出\(1\)号点到每辆车的最短路径，有一个性质：最短路径不同的点不会同时同向进入某条边。所以将最短路径相同的点归成一类，同时处理这些点，找出那些最短路径的边，设流量为\(1\)，然后跑一次最大流，然后每一类的最大流相加就是答案。

时间复杂度：难以估计，大胆写吧

D - Factors

题目描述：设\(f(n)\)表示\(n\)分解质因数后有多少种不同的排列，如\(f(20)=3\)，因\(f(20)=2 \cdot 2 \cdot 5=2 \cdot 5 \cdot 2=5 \cdot 2 \cdot 2\)。给出一个数\(k\)，求出一个最小的\(n\)，使得\(f(n)=k\)。

solution
设\(a_i\)表示\(n\)的每个质因数的个数。
\[f(n)=\frac{(\sum a_i)!}{\prod a_i!}\]
设\(n'=np^s, n \nmid p\)
\[f(n')=\frac{(\sum a_i +s)!}{\prod a_i! \times s!}\]
\[=\frac{(\sum a_i)! \cdot (\sum a_i +1) \cdot ... \cdot (\sum a_i +s)}{\prod a_i! \times s!}\]
\[=f(n) \cdot C_{\sum a_i +s}^{s}\]

所以直接搜索，质因数肯定是取最小的那些。貌似有答案不多。

时间复杂度：不会算。

F - Low Power

题目描述：有\(n\)个机器，每个机器有两个芯片，每个芯片会有\(k\)个电池，给出\(2nk\)个电池，分配这些电池，使得所有机器的两个芯片的电池最小值的差的最大值最小，输出这个值。

solution
先将电池从小到大排序。二分答案，显然每台机器的两个芯片的最小电池一定是相邻的电池，所以贪心分配就好。

时间复杂度：\(O(nlog10^9)\)

H - Матрёшка

题目描述：有\(n\)个排成一行的俄罗斯套娃，每个套娃有一个大小，一套完整的套娃的大小是从\(1\)到\(m\)(随便一个数)的连续整数，小的放在大的里面。现在将这\(n\)个套娃套成若干套完整的套娃，每次只能将相邻的套娃套在一起，一旦一个套娃变成一组套娃中的一个，则它最终不会变成别的组的套娃。问最少需要几次打开操作。如合并\([1, 2, 6]\)与\([4]\)，需要打开\(6\)和\(4\)的盖子。

solution
显然，一套套娃一定是连续的一段全排列，所以可以区间dp来分割区间成多个全排列。然后考虑一个全排列需要多少次打开操作来套成一套套娃。
这又可以用一个区间dp来求解，问题是合并两套不完整的套娃的最少操作，假设两套套娃最小的大小为\(A, B\)，若\(A<B\)，则\(A\)那套中小于\(B\)的那些套娃不用打开，反之有类似的结论，其它的套娃都要打开。

时间复杂度：\(O(n^3)\)

I - Pirate Chest

题目描述：有一个\(n \times m\)的水池，给出每一格水池的深度，现要将一个底面的长和宽不超过\(a\)和\(b\)的长方体放入池中，使得长方体严格在水面以下，当然长方体放进去后水面会上升。求出长方体体积的最大值。

solution
假设水面不会上升。则某个子矩阵上的长方体的体积为该子矩阵中的最小值乘子矩阵的面积。设\(A(h)\)表示最小值为\(h\)的子矩阵的最大面积（当然要考虑\(a, b\))，这个函数可以在\(O(n^3)\)的时间内求出。（枚举某两列，表示子矩阵的列的范围，压缩成一列，即每行只保留最小值，算出第\(i\)行的最小值为子矩阵最小值的范围）
事实上并不需要记录\(A(h)\)，当算出\(A(h)\)时，\(O(1)\)就能算出它能高出原水面的高度，更新答案即可。

时间复杂度：\(O(n^3)\)

J - Pollution Solution

题目描述：求一个半圆与一个多边形的交的面积。

solution
由于那个多边形也只在半圆的那边，所以直接求多边形与圆的交也是可以。直接上模板。

时间复杂度：\(O(n)\)