【UOJ 179】 #179. 线性规划 （单纯形法）

http://uoj.ac/problem/179

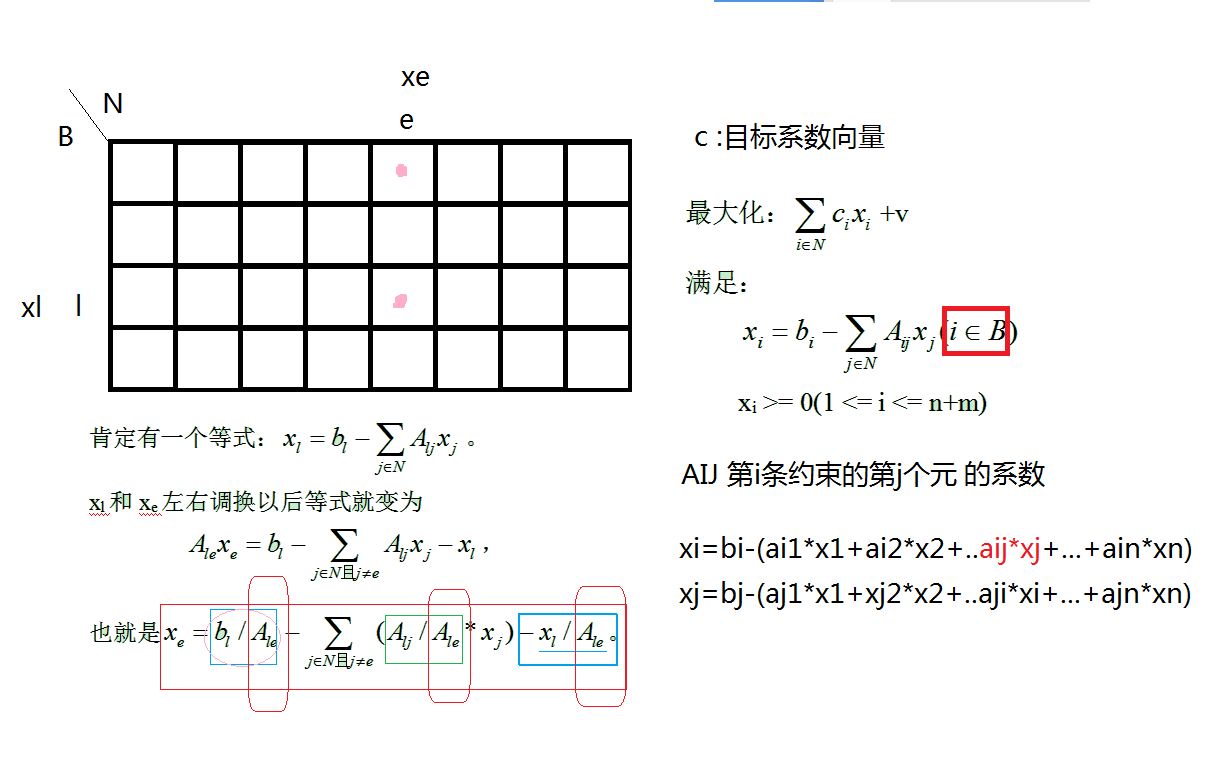
补充那一列修改方法：

对于第i行：

　　$$xi=bi-\sum Aij*xj$$

　　　　　    $$=bi-\sum_{j!=e} Aij*xj-Aie*xe$$

Pivot后应该是： $$=bi-\sum_{j!=e} Aij*xj-Aie*xl$$

假设第l行已经算对转轴后的系数

则$$xl=bl-\sum Alj*xj$$

所以$$xi=bi-\sum_{j!=e} Aij*xj-Aie*(bl-\sum Alj*xj)$$

$$=bi-Aie*bl-\sum_{j!=e}(Aij-Aie*Alj)*xj-(0-Aie*Alj*xj)$$

观察变化：

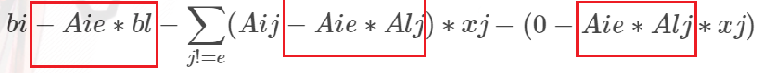
可以看出，所有系数只要-Aie*Alj就好了的。因为Aie会在过程中变化，所以一开始先存起来，然后置为0。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<ctime>
using namespace std;
#define Maxn 25
const double eps=0.00000001,INF=1e15;

int n,m;

int id[Maxn*2];
double a[Maxn][Maxn];
//第一维是限制，B集合
//第二维是元素，N集合
//a[0][xx] -> c 目标函数系数
//a[xx][0] -> b 限制等式常数
//a[xx][yy] -> A 限制等式系数向量
//最大化 sigma(ci*xi),i属于N
//限制 xj=bj-sigma(aji*xi) ,j属于B

double myabs(double x) {return x>0?x:-x;}

void Pivot(int l,int e)
{
	//转轴l和e
	swap(id[n+l],id[e]);
	double t=a[l][e];a[l][e]=1;
	for(int j=0;j<=n;j++) a[l][j]/=t;
	for(int i=0;i<=m;i++) if(i!=l&&myabs(a[i][e])>eps)
    {
		t=a[i][e];a[i][e]=0;
		for(int j=0;j<=n;j++) a[i][j]-=a[l][j]*t;
	}
}

//初始化-辅助问题
bool init()
{
	while(1)
	{
		int e=0,l=0;
		for(int i=1;i<=m;i++) if(a[i][0]<-eps&&(!l||(rand()&1))) l=i;
		if(!l) break;
		for(int j=1;j<=n;j++) if(a[l][j]<-eps&&(!e||(rand()&1))) e=j;
		if(!e) {printf("Infeasible\n");return 0;}
		Pivot(l,e);
	}
	return 1;
}

//最优化
bool simplex()
{
	while(1)
	{
		int l=0,e=0;double mn=INF;
		for(int j=1;j<=n;j++)
		  if(a[0][j]>eps) {e=j;break;}
		if(!e) break;//如果目标变量c都小于0 找到答案
		for(int i=1;i<=m;i++) if(a[i][e]>eps&&a[i][0]/a[i][e]<mn)
			mn=a[i][0]/a[i][e],l=i;//找a[i][0]/a[i][e]最小的i进行转轴
		if(!l) {printf("Unbounded\n");return 0;}
		//如果所有的a[i][e]都小于0，说明最优值正无穷
		Pivot(l,e);
	}
	return 1;
}

double ans[Maxn];

int main()
{
	srand(time(0));
	int t;
	scanf("%d%d%d",&n,&m,&t);
	for(int i=1;i<=n;i++) scanf("%lf",&a[0][i]);
	for(int i=1;i<=m;i++)
	{
	  for(int j=1;j<=n;j++) scanf("%lf",&a[i][j]);
		scanf("%lf",&a[i][0]);
	}
	for(int i=1;i<=n;i++) id[i]=i;
	if(init()&&simplex())
	{
		printf("%.8lf\n",-a[0][0]);
		if(t)
		{
			for(int i=1;i<=m;i++) ans[id[n+i]]=a[i][0];
			for(int i=1;i<=n;i++) printf("%.8lf ",ans[i]);
		}
	}
	return 0;
}

　　

2017-03-14 21:01:07