jenkins pipelines 简介

1. 简介：A pipeline就是软件和质量保证进程中的一部分中的自动化连续操作。它可以看成是一连串的脚本。

• 操作组：就是把一系统的操作可以合成一个个的步骤，如果一个步骤失败，那么后续步骤便不会执行。
• 可见性：这个进程的所有方面都是可见性的，它有助于快速地分析失败原因并提高团队合作。
• 反馈：当有问题发生时，团队的成员能快速的得知并进行反馈。

2. Pipeline 结构

Jenkins pipeline包含两类元素：stages和steps。 如下图：

step: 代表单一的操作（告诉Jenkins做什么，比如，代码从仓库检出，执行脚本）

stage: 等于一系列step的组合，，常常用来表示Jenkins pipeline 进程的可示化。（如Build, Test 和Deploy）

二. 多阶段的 Hello World案例

代码如下：

pipeline {
      agent any
      stages {
           stage('First Stage') {
                steps {
                     echo 'Step 1. Hello World'
                }
           }
           stage('Second Stage') {
                steps {
                     echo 'Step 2. Second time Hello'
                     echo 'Step 3. Third time Hello'
                }
           }
      }

}

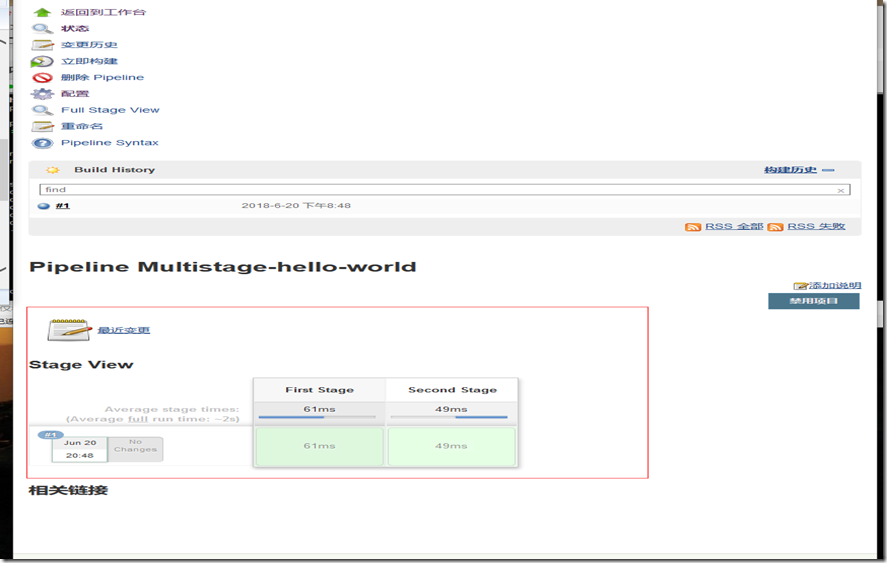
2. 点击立即构建，显示如下：