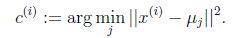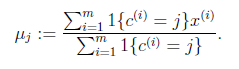Kmeans聚类算法
K-means也是聚类算法中最简单的一种了,但是里面包含的思想却是不一般。最早我使用并实现这个算法是在学习韩爷爷那本数据挖掘的书中,那本书比较注重应用。看了Andrew Ng的这个讲义后才有些明白K-means后面包含的EM思想。
聚类属于无监督学习,以往的回归、朴素贝叶斯、SVM等都是有类别标签y的,也就是说样例中已经给出了样例的分类。而聚类的样本中却没有给定y,只有特征x,比如假设宇宙中的星星可以表示成三维空间中的点集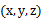 。聚类的目的是找到每个样本x潜在的类别y,并将同类别y的样本x放在一起。比如上面的星星,聚类后结果是一个个星团,星团里面的点相互距离比较近,星团间的星星距离就比较远了。
。聚类的目的是找到每个样本x潜在的类别y,并将同类别y的样本x放在一起。比如上面的星星,聚类后结果是一个个星团,星团里面的点相互距离比较近,星团间的星星距离就比较远了。
在聚类问题中,给我们的训练样本是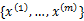 ,每个
,每个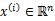 ,没有了y。
,没有了y。
K-means算法是将样本聚类成k个簇(cluster),具体算法描述如下:
|
1、 随机选取k个聚类质心点(cluster centroids)为 2、 重复下面过程直到收敛 { 对于每一个样例i,计算其应该属于的类
对于每一个类j,重新计算该类的质心
} |
K是我们事先给定的聚类数, 代表样例i与k个类中距离最近的那个类,
代表样例i与k个类中距离最近的那个类, 的值是1到k中的一个。质心
的值是1到k中的一个。质心 代表我们对属于同一个类的样本中心点的猜测,拿星团模型来解释就是要将所有的星星聚成k个星团,首先随机选取k个宇宙中的点(或者k个星星)作为k个星团的质心,然后第一步对于每一个星星计算其到k个质心中每一个的距离,然后选取距离最近的那个星团作为
代表我们对属于同一个类的样本中心点的猜测,拿星团模型来解释就是要将所有的星星聚成k个星团,首先随机选取k个宇宙中的点(或者k个星星)作为k个星团的质心,然后第一步对于每一个星星计算其到k个质心中每一个的距离,然后选取距离最近的那个星团作为 ,这样经过第一步每一个星星都有了所属的星团;第二步对于每一个星团,重新计算它的质心
,这样经过第一步每一个星星都有了所属的星团;第二步对于每一个星团,重新计算它的质心 (对里面所有的星星坐标求平均)。重复迭代第一步和第二步直到质心不变或者变化很小。
(对里面所有的星星坐标求平均)。重复迭代第一步和第二步直到质心不变或者变化很小。
下图展示了对n个样本点进行K-means聚类的效果,这里k取2。

K-means面对的第一个问题是如何保证收敛,前面的算法中强调结束条件就是收敛,可以证明的是K-means完全可以保证收敛性。下面我们定性的描述一下收敛性,我们定义畸变函数(distortion function)如下:

J函数表示每个样本点到其质心的距离平方和。K-means是要将J调整到最小。假设当前J没有达到最小值,那么首先可以固定每个类的质心 ,调整每个样例的所属的类别
,调整每个样例的所属的类别 来让J函数减少,同样,固定
来让J函数减少,同样,固定 ,调整每个类的质心
,调整每个类的质心 也可以使J减小。这两个过程就是内循环中使J单调递减的过程。当J递减到最小时,
也可以使J减小。这两个过程就是内循环中使J单调递减的过程。当J递减到最小时, 和c也同时收敛。(在理论上,可以有多组不同的
和c也同时收敛。(在理论上,可以有多组不同的 和c值能够使得J取得最小值,但这种现象实际上很少见)。
和c值能够使得J取得最小值,但这种现象实际上很少见)。
由于畸变函数J是非凸函数,意味着我们不能保证取得的最小值是全局最小值,也就是说k-means对质心初始位置的选取比较感冒,但一般情况下k- means达到的局部最优已经满足需求。但如果你怕陷入局部最优,那么可以选取不同的初始值跑多遍k-means,然后取其中最小的J对应的 和c输出。
和c输出。
下面累述一下K-means与EM的关系,首先回到初始问题,我们目的是将样本分成k个类,其实说白了就是求每个样例x的隐含类别y,然后利用隐含类别将 x归类。由于我们事先不知道类别y,那么我们首先可以对每个样例假定一个y吧,但是怎么知道假定的对不对呢?怎么评价假定的好不好呢?我们使用样本的极大 似然估计来度量,这里是就是x和y的联合分布P(x,y)了。如果找到的y能够使P(x,y)最大,那么我们找到的y就是样例x的最佳类别了,x顺手就聚 类了。但是我们第一次指定的y不一定会让P(x,y)最大,而且P(x,y)还依赖于其他未知参数,当然在给定y的情况下,我们可以调整其他参数让 P(x,y)最大。但是调整完参数后,我们发现有更好的y可以指定,那么我们重新指定y,然后再计算P(x,y)最大时的参数,反复迭代直至没有更好的y 可以指定。
这个过程有几个难点,第一怎么假定y?是每个样例硬指派一个y还是不同的y有不同的概率,概率如何度量。第二如何估计P(x,y),P(x,y)还可能依赖很多其他参数,如何调整里面的参数让P(x,y)最大。这些问题在以后的篇章里回答。
这里只是指出EM的思想,E步就是估计隐含类别y的期望值,M步调整其他参数使得在给定类别y的情况下,极大似然估计P(x,y)能够达到极大值。然后在其他参数确定的情况下,重新估计y,周而复始,直至收敛。
上面的阐述有点费解,对应于K-means来说就是我们一开始不知道每个样例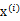 对应隐含变量也就是最佳类别
对应隐含变量也就是最佳类别 。最开始可以随便指定一个
。最开始可以随便指定一个 给它,然后为了让P(x,y)最大(这里是要让J最小),我们求出在给定c情况下,J最小时的
给它,然后为了让P(x,y)最大(这里是要让J最小),我们求出在给定c情况下,J最小时的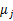 (前面提到的其他未知参数),然而此时发现,可以有更好的
(前面提到的其他未知参数),然而此时发现,可以有更好的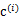 (质心与样例
(质心与样例 距离最小的类别)指定给样例
距离最小的类别)指定给样例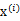 ,那么
,那么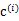 得到重新调整,上述过程就开始重复了,直到没有更好的
得到重新调整,上述过程就开始重复了,直到没有更好的 指定。这样从K-means里我们可以看出它其实就是EM的体现,E步是确定隐含类别变量
指定。这样从K-means里我们可以看出它其实就是EM的体现,E步是确定隐含类别变量 ,M步更新其他参数
,M步更新其他参数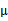 来 使J最小化。这里的隐含类别变量指定方法比较特殊,属于硬指定,从k个类别中硬选出一个给样例,而不是对每个类别赋予不同的概率。总体思想还是一个迭代优 化过程,有目标函数,也有参数变量,只是多了个隐含变量,确定其他参数估计隐含变量,再确定隐含变量估计其他参数,直至目标函数最优。
来 使J最小化。这里的隐含类别变量指定方法比较特殊,属于硬指定,从k个类别中硬选出一个给样例,而不是对每个类别赋予不同的概率。总体思想还是一个迭代优 化过程,有目标函数,也有参数变量,只是多了个隐含变量,确定其他参数估计隐含变量,再确定隐含变量估计其他参数,直至目标函数最优。
本文来源链接:
Kmeans聚类算法的更多相关文章
- K-Means 聚类算法
K-Means 概念定义: K-Means 是一种基于距离的排他的聚类划分方法. 上面的 K-Means 描述中包含了几个概念: 聚类(Clustering):K-Means 是一种聚类分析(Clus ...
- k-means聚类算法python实现
K-means聚类算法 算法优缺点: 优点:容易实现缺点:可能收敛到局部最小值,在大规模数据集上收敛较慢使用数据类型:数值型数据 算法思想 k-means算法实际上就是通过计算不同样本间的距离来判断他 ...
- K-Means 聚类算法原理分析与代码实现
前言 在前面的文章中,涉及到的机器学习算法均为监督学习算法. 所谓监督学习,就是有训练过程的学习.再确切点,就是有 "分类标签集" 的学习. 现在开始,将进入到非监督学习领域.从经 ...
- Kmeans聚类算法原理与实现
Kmeans聚类算法 1 Kmeans聚类算法的基本原理 K-means算法是最为经典的基于划分的聚类方法,是十大经典数据挖掘算法之一.K-means算法的基本思想是:以空间中k个点为中心进行聚类,对 ...
- 机器学习六--K-means聚类算法
机器学习六--K-means聚类算法 想想常见的分类算法有决策树.Logistic回归.SVM.贝叶斯等.分类作为一种监督学习方法,要求必须事先明确知道各个类别的信息,并且断言所有待分类项都有一个类别 ...
- 转载: scikit-learn学习之K-means聚类算法与 Mini Batch K-Means算法
版权声明:<—— 本文为作者呕心沥血打造,若要转载,请注明出处@http://blog.csdn.net/gamer_gyt <—— 目录(?)[+] ================== ...
- 沙湖王 | 用Scipy实现K-means聚类算法
沙湖王 | 用Scipy实现K-means聚类算法 用Scipy实现K-means聚类算法
- Matlab中K-means聚类算法的使用(K-均值聚类)
K-means聚类算法采用的是将N*P的矩阵X划分为K个类,使得类内对象之间的距离最大,而类之间的距离最小. 使用方法:Idx=Kmeans(X,K)[Idx,C]=Kmeans(X,K) [Idx, ...
- 运用三角不等式加速Kmeans聚类算法
运用三角不等式加速Kmeans聚类算法 引言:最近在刷<数据挖掘导论>,第九章, 9.5.1小节有提到,可以用三角不等式,减少不必要的距离计算,从而达到加速聚类算法的目的.这在超大数据量的 ...
- 视觉SLAM之词袋(bag of words) 模型与K-means聚类算法浅析
原文地址:http://www.cnblogs.com/zjiaxing/p/5548265.html 在目前实际的视觉SLAM中,闭环检测多采用DBOW2模型https://github.com/d ...
随机推荐
- TOMcat9 免安装版的配置
在这里默认大家都安装了jdk并且配置了java的环境,网上教程很多. 在tomcat官网(http://tomcat.apache.org/download-90.cgi)上下载和自己系统匹配的安装包 ...
- 1张图看懂RAID功能,6张图教会配置服务器【转】
RAID 包含一组或者一个集合甚至一个阵列.使用一组磁盘结合驱动器组成 RAID 阵列或 RAID 集.将至少两个磁盘连接到一个 RAID 控制器,而成为一个逻辑卷,也可以将多个驱动器放在一个组中.一 ...
- LightOJ 1095 Arrange the Numbers-容斥
给出n,m,k,求1~n中前m个正好有k个在原来位置的种数(i在第i个位置) 做法:容斥,先选出k个放到原来位置,然后剩下m-k个不能放到原来位置的,用0个放到原来位置的,有C(m-k,0)*(n-k ...
- ACdream 1007
input T <=10 n k n<=1000 k<=10^18 a1,a2,...an | ...
- 虚拟机Q&A
Q1:虚拟机运行一段时间后,各个版本的第一台虚拟机容量变大,增大容量可以接受 原因:不详 解决方法:用备份镜像替换当前镜像 1.1G Jun 24 17:07 win7_sp1_32_0.qcow2 ...
- css3选择器:nth-child和nth-of-type之间的差别
<section> <p>我是第1个p标签</p> <p>我是第2个p标签</p> </section> 然后对应2个选择器对应 ...
- 使用PowerDesigner创建mysql数据库表图
使用PowerDesigner 建数据库表. 一直很忙,没有时间写东西.这次搞点会声会色的,嘿嘿 此技能为项目经理必备技能. 本次主角: 1.在workspace下建立一项目: physical da ...
- Spring 创建 IOC 容器 ClassPathXmlApplicationContext 类
一.ClassPathXmlApplicationContext 类的作用 在 Java 环境中使用 Spring 时,需要用 new ClassPathXmlApplicationContext(c ...
- Maven搭建springMVC+spring+hibernate环境
这次不再使用struts2做控制器,采用spring自己的springMVC框架实现. 首先,改写pom.xml文件,不需要struts2的相关jar了. pom.xml <project xm ...
- YII使用PHPExcel导入Excel文件的方法
1.下载phpexcel,将压缩包中的classes复制到protected/extensions下并修改为PHPExcel. 2.修改YII配置文件config/main.php 'import'= ...

 。
。