x01.BSheepTree: 树

数据结构，无外乎三：

1. 一对一，线性表，数组是也；

2. 一对多，树，菜单是也；

3. 多对多，图，网络是也。

涉及到树，有一个平衡的问题，左旋转，右旋转，转得人晕晕乎乎。好在陈广的《数据结构C#描述》讲解非常详尽，值得一读。对照该书的例子，采用反编译的手段，写了个小程序，主要的目的是为了学习方便，也便于自己查找复习，无他。源代码可到置顶随笔 x01.Download => book => 2016 中下载：x01.BSheepTree.zip；其运行效果图如下：

略作修改，便成为红黑树，解释参看：红黑树 其运行效果图如下：

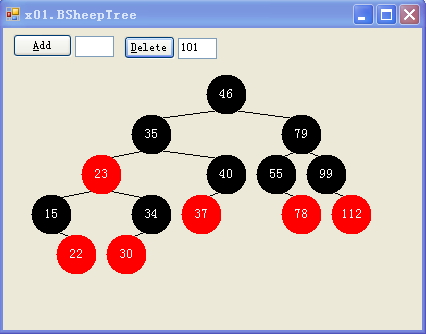
关键代码如下：

/**
 * RedBlackTree.cs (c) 2015 by x01
 */
using System;
using System.Diagnostics;
using System.Text;

namespace x01.BSheepTree
{
    /// <summary>
    /// Description of RedBlackTree.
    /// </summary>
    public class RedBlackTree : IBinaryTree
    {
        public static readonly bool Red = true;
        public static readonly bool Black = false;

        public class RNode : INode
        {
            public int Key { get; set; }
            public int Value { get; set; }
            public RNode Parent { get; set; }
            public RNode Left { get; set; }
            public RNode Right { get; set; }
            public RNode Sibling
            {
                get {
                    RNode sibling = null;
                    if (Parent != null && this == Parent.Left)
                        sibling = Parent.Right;
                    else if (Parent != null && this == Parent.Right)
                        sibling = Parent.Left;
                    return sibling;
                }
            }
            public RNode GrandParent
            {
                get {
                    if (Parent != null)
                        return Parent.Parent;
                    return null;
                }
            }
            public RNode Uncle
            {
                get {
                    RNode uncle = null;
                    if (GrandParent != null) {
                        if (Parent == GrandParent.Left)
                            uncle = GrandParent.Right;
                        else if (Parent == GrandParent.Right)
                            uncle = GrandParent.Left;
                    }
                    return uncle;
                }
            }
            public bool Color { get; set; }

            public RNode(int key, int value)
            {
                this.Key = key;
                this.Value = value;
                Color = Red;
                Parent = Left = Right = null;
            }            

            public RNode LeftMost
            {
                get {
                    var node = this;
                    while (node != null && node.Left != null ) {
                        node = node.Left;
                    }
                    return node;
                }
            }

            public int Data {
                get {
                    return (int)Value;
                }
            }

            INode INode.Left {
                get {
                    return (INode)Left;
                }
            }

            INode INode.Right {
                get {
                    return (INode)Right;
                }
            }
        }

        RNode root = null;

        public void Insert(int key, int value)
        {
            root = Insert(root, key, value);
            root.Color = Black;
            //SetParent();
        }
        RNode Insert(RNode node, int key, int value)
        {
            if (node == null)
                return new RNode(key, value);
            int cmp = key.CompareTo(node.Key);
            if (cmp < )
                node.Left = Insert(node.Left, key, value);
            else if (cmp > )
                node.Right = Insert(node.Right, key, value);
            else
                node.Value = value;

            node = Balance(node);

            return node;
        }

        RNode Balance(RNode node)
        {
            if (node != null) {
                if (IsRed(node.Right) && !IsRed(node.Left)) node = RotateLeft(node);
                if (IsRed(node.Left) && IsRed(node.Left.Left)) node = RotateRight(node);
                if (IsRed(node.Left) && IsRed(node.Right)) FlipColor(node);
            }
            return node;
        }

        void SetParent()
        {
            SetParent(root);
        }
        void SetParent(RNode node)
        {
            if (node != null) {
                if (node.Left != null) {
                    node.Left.Parent = node;
                    SetParent(node.Left);
                }
                if (node.Right != null) {
                    node.Right.Parent = node;
                    SetParent(node.Right);
                }
            }
        }

        void Replace(RNode oldNode, RNode newNode)
        {
            if (oldNode == null || newNode == null)
                throw new Exception();

            oldNode.Key = newNode.Key;
            oldNode.Value = newNode.Value;
        }

        public RNode GetNode(int key)
        {
            return GetNode(root, key);
        }
        RNode GetNode(RNode node, int key)
        {
            while (node != null) {
                int cmp = key.CompareTo(node.Key);
                if (cmp < ) node = node.Left;
                else if (cmp > ) node = node.Right;
                else return node;
            }
            return null;
        }

        public bool IsEmpty { get { return root == null; } }

        public void DeleteMin()
        {
            if (IsEmpty) return;
            if (!IsRed(root.Left) && !IsRed(root.Right))
                root.Color = Red;
            root = DeleteMin(root);
            if (!IsEmpty) root.Color = Black;
        }

        RNode DeleteMin(RNode node)
        {
            if (node != null && node.Left == null)
                return null;

            if (!IsRed(node.Left) && !IsRed(node.Left.Left))
                node = MoveRedLeft(node);

            node.Left = DeleteMin(node.Left);

            return Balance(node);
        }

        RNode MoveRedLeft(RNode node)
        {
            FlipColor(node);
            if (IsRed(node.Right.Left)) {
                node.Right = RotateRight(node.Right);
                node = RotateLeft(node);
                FlipColor(node);
            }
            return node;
        }

        RNode MoveRedRight(RNode node)
        {
            FlipColor(node);
            if (IsRed(node.Left.Left)) {
                node = RotateRight(node);
                FlipColor(node);
            }
            return node;
        }

        public void DeleteMax()
        {
            if (IsEmpty) throw new Exception();
            if (!IsRed(root.Left) && !IsRed(root.Right))
                root.Color = Red;
            root = DeleteMax(root);
            if (!IsEmpty) root.Color = Black;
        }

        RNode DeleteMax(RNode node)
        {
            if (IsRed(node.Left))
                node = RotateRight(node);
            if (node.Right == null)
                return null;
            if (!IsRed(node.Right) && !IsRed(node.Right.Left))
                node = MoveRedRight(node);
            node.Right = DeleteMax(node.Right);
            return Balance(node);
        }

        public void Delete(int key)
        {
            var node = GetNode(key);
            if (node == null) return;

            if (!IsRed(node.Left) && !IsRed(node.Right))
                root.Color = Red;

            root = Delete(root, key);
            if (!IsEmpty) root.Color = Black;
        }

        RNode Delete(RNode node, int key)
        {
            if (key.CompareTo(node.Key) < ) {
                if (!IsRed(node.Left) && !IsRed(node.Left.Left))
                    node = MoveRedLeft(node);
                node.Left = Delete(node.Left, key);
            } else {
                if (IsRed(node.Left))
                    node = RotateRight(node);
                if (key.CompareTo(node.Key) ==  && node.Right == null)
                    return null;
                if (!IsRed(node.Right) && !IsRed(node.Right.Left))
                    node = MoveRedRight(node);
                if (key.CompareTo(node.Key) == ) {
                    var x = Min(node.Right);
                    node.Key = x.Key;
                    node.Value = x.Value;
                    node.Right = DeleteMin(node.Right);
                } else {
                    node.Right = Delete(node.Right, key);
                }
            }
            return Balance(node);
        }

        RNode Min(RedBlackTree.RNode node)
        {
            if (node.Left == null) return node;
            else return Min(node.Left);
        }

        void FlipColor(RNode node)
        {
            node.Color = !node.Color;
            node.Left.Color = !node.Left.Color;
            node.Right.Color = !node.Right.Color;
        }

        RNode RotateRight(RNode node)
        {
            RNode left = node.Left;
            node.Left = left.Right;
            left.Right = node;
            left.Color = node.Color;
            node.Color = Red;
            return left;
        }

        RNode RotateLeft(RNode node)
        {
            RNode right = node.Right;
            node.Right = right.Left;
            right.Left = node;
            right.Color = node.Color;
            node.Color = Red;
            return right;
        }

        bool IsRed(RNode node)
        {
            return node != null && node.Color == Red;
        }

        public int Count
        {
            get { return _Count(root); }
        }
        int _Count(RNode node)
        {
            if (node != null)
                return _Count(node.Left) + _Count(node.Right) + ;
            return ;
        }

        #region Test

        void Print()
        {
            Print(root);
        }
        void Print(RNode node)
        {
            if (node != null) {
                string clr = node.Color ? "R" : "B";
                Console.Write("{0}{1} => ", node.Key, clr);
                Print(node.Left);
                Print(node.Right);
            }
        }
        internal static void Test()
        {
            var tree = new RedBlackTree();
            for (int i = ; i < ; i++) {
                tree.Insert(i,i);
            }
            tree.Delete();
            tree.Print();
            Console.WriteLine();
        }

        public INode Head {
            get {
                return (INode)root;
            }
        }
        public bool Add(int data)
        {
            Insert((int)data, (int)data);
            return true;
        }
        public bool Remove(int data)
        {
            Delete((int)data);
            return true;
        }

        #endregion
    }
}

RedBlackTree.cs