noip2013Day2T3-华容道【一个蒟蒻的详细题解】

描述

小 B 最近迷上了华容道，可是他总是要花很长的时间才能完成一次。于是，他想到用编程来完成华容道：给定一种局面，华容道是否根本就无法完成，如果能完成，最少需要多少时间。

小 B 玩的华容道与经典的华容道游戏略有不同，游戏规则是这样的：

1. 在一个 n*m 棋盘上有 n*m 个格子，其中有且只有一个格子是空白的，其余 n*m-1个格子上每个格子上有一个棋子，每个棋子的大小都是 1*1 的；

2. 有些棋子是固定的，有些棋子则是可以移动的；

3. 任何与空白的格子相邻（有公共的边）的格子上的棋子都可以移动到空白格子上。 游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。

给定一个棋盘，游戏可以玩 q 次，当然，每次棋盘上固定的格子是不会变的，但是棋盘上空白的格子的初始位置、指定的可移动的棋子的初始位置和目标位置却可能不同。第 i 次玩的时候，空白的格子在第 EXi行第 EYi 列，指定的可移动棋子的初始位置为第 SXi 行第 SYi 列，目标位置为第 TXi 行第 TYi 列。

假设小 B 每秒钟能进行一次移动棋子的操作，而其他操作的时间都可以忽略不计。请你告诉小 B 每一次游戏所需要的最少时间，或者告诉他不可能完成游戏。

格式

输入格式

第一行有 3 个整数，每两个整数之间用一个空格隔开，依次表示 n、m 和 q；

接下来的 n 行描述一个 n*m 的棋盘，每行有 m 个整数，每两个整数之间用一个空格隔开，每个整数描述棋盘上一个格子的状态，0 表示该格子上的棋子是固定的，1 表示该格子上的棋子可以移动或者该格子是空白的。

接下来的 q 行，每行包含 6 个整数依次是 EXi、EYi、SXi、SYi、TXi、TYi，每两个整数之间用一个空格隔开，表示每次游戏空白格子的位置，指定棋子的初始位置和目标位置。

输出格式

输出有 q 行，每行包含 1 个整数，表示每次游戏所需要的最少时间，如果某次游戏无法完成目标则输出−1。

样例1

样例输入1

 

3 4 2
0 1 1 1
0 1 1 0
0 1 0 0
3 2 1 2 2 2
1 2 2 2 3 2

样例输出1

 

2
-1

限制

每个测试点1s。

提示

样例说明

棋盘上划叉的格子是固定的，红色格子是目标位置，圆圈表示棋子，其中绿色圆圈表示目标棋子。

1. 第一次游戏，空白格子的初始位置是 (3, 2)（图中空白所示），游戏的目标是将初始位置在(1, 2)上的棋子（图中绿色圆圈所代表的棋子）移动到目标位置(2, 2)（图中红色的格子）上。

   移动过程如下:

   

2. 第二次游戏，空白格子的初始位置是（1, 2）（图中空白所示），游戏的目标是将初始位置在（2, 2）上的棋子（图中绿色圆圈所示）移动到目标位置 (3, 2)上。

   

   要将指定块移入目标位置，必须先将空白块移入目标位置，空白块要移动到目标位置，必然是从位置（2，2）上与当前图中目标位置上的棋子交换位置，之后能与空白块交换位置的只有当前图中目标位置上的那个棋子，因此目标棋子永远无法走到它的目标位置，游戏无法完成。

数据范围

对于 30%的数据，1 ≤ n, m ≤ 10，q = 1；
对于 60%的数据，1 ≤ n, m ≤ 30，q ≤ 10；
对于 100%的数据，1 ≤ n, m ≤ 30，q ≤ 500。

题解

就是啊，公子还是把这道题过了……【虽然抄了题解的思路但是公子没有抄代码啊】

嗯，用蒟蒻的语言给蒟蒻碰上的人用蒟蒻的方式讲讲吧……

windows画图是神器，嗯。

【1】首先我们需要一个曹操华容道，然后我们观察棋子的性质。

（1）我们可以把移动棋子当做移动白格【显然】

（2）我们只需要关注的是起始棋子【显然】

（3）结合（1）（2）我们需要拿白格子去给起始棋子铺路【显然】

（4）那么如果起始棋子旁边没有白格子时，我们需要把白格子搞到它旁边。【显然】

（5）那么（4）之后我们如果要把起始棋子（在不与上一次移动相反的情况下）向某一方向移动时，我们要把白格子铺在当前棋子位置这一方向【……显然？】

（6）（5）中的操作白格子永远在当前起始棋子位置的四周。【显然？】

【暴搜超时的要点其实是（6），当瞎搞的时候算了很多很多很多遍的让白格子从(x,y)的从上到右，从上到下，从下到左……这样的白格子铺路移动】

（7）那么所有位置可能是放棋子的位置。【显然】

（8）预处理所有位置上下左右四个方向到另外的上下左右四个方向。【………………】

【1】的（4）实现方法：

空白格子对起始格子的四周进行暴搜路径大小。

（9）（8）的方法同上，但暴搜不能经过（x,y）原位置,那就相当于重复移动。

这两个都是非常简单的宽搜。

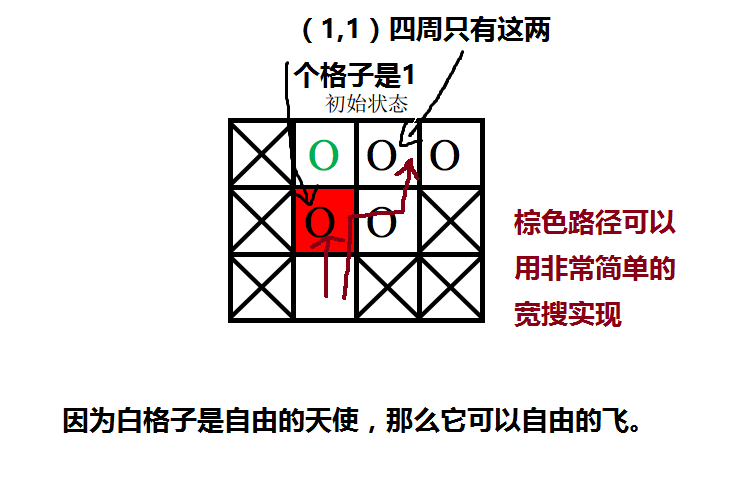
嗯。我都讲到这个份上了，预处理就可以结束了。

（因为这个图不优美，并不一定是曼哈顿距离。）

【2】我们还需要一个关羽最短路。

（1）为什么需要最短路呢，因为题里说要求最短路【显然】

（2）这张图很工整，可以跑spfa【显然】

（3）上面两句都是废话【……】

（4）我们初始塞进去初始棋子上下左右的四个状态【显然】

（5）我们移动的时候还是需要白格子铺路的代价【显然】

（6）然而我们已经在【1】预处理出来了！【鼓掌】

（7）但是我们发现对于(x,y),从(x-1,y)和(y+1,x)移动来的【诸如此类的】并不一定是一个状态（白格子的方位不同）。【哦QAQ】

（8）但是由于图只有30*30那么大，所以我们多开一维记录方向。【嘿嘿嘿】

（9）然后就变成了一个裸的spfa，带了方向转移即可。【嘿嘿嘿】

【spfa那么简单我拒绝画图。】

题做完了。

代码量↑↑↑……自己写写看吧。

不要抄我的，我写的丑，出门可以转到很多代码优美的神犇那里。

还有我题解写得那么详尽就不要抄了orz。

【不要看↓，这是一个蒟蒻存代码的地方，不要伤害我了QAQ】

 #include <iostream>
 #include <string.h>
 #include <cstdlib>
 #include <cstdio>
 #include <algorithm>
 #include <cstring>
 #include <vector>
 #include <ctime>
 #include <queue>
 //#define ivorysi
 #define mo 10007
 #define siji(i,x,y) for(int i=(x);i<=(y);i++)
 #define gongzi(j,x,y) for(int j=(x);j>=(y);j--)
 #define xiaosiji(i,x,y) for(int i=(x);i<(y);i++)
 #define sigongzi(j,x,y) for(int j=(x);j>(y);j--)
 #define ivory(i,x) for(int i=head[x];i;i=edge[i].next)
 #define pii pair<int,int>
 #define fi first
 #define se second
 #define inf 0x5f5f5f5f
 typedef long long ll;
 using namespace std;
 struct data{
     int x,y,k,step;
 };
 struct node {
     int x,y,k;
 };
 int dirx[]={,-,,,},diry[]={,,,-,};
 int op[]={,,,,};
 int n,m,q;
 queue<data> q1;
 queue<node> q2;
 int graph[][],wmove[][][][];
 int dist[][][];
 bool vis[][][];
 bool vis1[][];
 int ex,ey,sx,sy,tx,ty;
 void pre(int x,int y) {//暴搜处理四周格子部分
     siji(i,,) {
         if(!graph[x+dirx[i]][y+diry[i]]) continue;
         siji(j,,) {
             if(i==j || wmove[x][y][i][j]) continue;
             int xx=x+dirx[j],yy=y+diry[j];
             if(!graph[xx][yy]) continue;
             siji(k,,n) siji(l,,m){
                 vis1[k][l]=;
             }
             while(!q1.empty()) q1.pop();
             q1.push((data){x+dirx[i],y+diry[i],i,});
             vis1[x+dirx[i]][y+diry[i]]=;
             int ans=-;
             while(!q1.empty()) {
                 data tmp=q1.front();q1.pop();
                 if(tmp.x==xx && tmp.y==yy) {ans=tmp.step;break;}
                 siji(l,,) {
                     if(l!=op[tmp.k]) {
                         int nx=tmp.x+dirx[l],ny=tmp.y+diry[l];
                         if((nx!=x || ny!=y ) && graph[nx][ny] &&(!vis1[nx][ny])) {
                             q1.push((data){nx,ny,l,tmp.step+});
                             vis1[nx][ny]=;
                         }
                     }
                 }
             }
             wmove[x][y][i][j]=wmove[x][y][j][i]=ans;
         }

     }
 }
 void pre_plain() {//处理ex,ey到sx,sy四周的部分
     siji(i,,) {
         int xx=sx+dirx[i],yy=sy+diry[i];
         if(!graph[xx][yy]) continue;
         while(!q1.empty()) q1.pop();
         int ans=inf;
         q1.push((data){ex,ey,,});

         siji(k,,n) siji(l,,m){
             vis1[k][l]=;
         }
         vis1[ex][ey]=;
         while(!q1.empty()) {

             data tmp=q1.front();q1.pop();
             if(tmp.x==xx && tmp.y==yy) {ans=tmp.step;break;}
             siji(l,,) {
                 if(l!=op[tmp.k]) {
                     int nx=tmp.x+dirx[l],ny=tmp.y+diry[l];
                     if((nx!=sx || ny!=sy) && graph[nx][ny] && (!vis1[nx][ny])) {
                         q1.push((data){nx,ny,l,tmp.step+});
                         vis1[nx][ny]=;
                     }
                 }
             }
         }
         if(ans<inf) {//顺手把状态塞进去
             dist[xx][yy][i]=ans+;
             vis[xx][yy][i]=;
             q2.push((node){xx,yy,i});
         }
     }
 }
 void solve() {
     while(!q2.empty()) q2.pop();
     siji(i,,n) siji(j,,m) siji(l,,){
         dist[i][j][l]=inf;
         vis[i][j][l]=;
     }
     pre_plain();
     int ans=inf;
     if(tx==sx && ty==sy) ans=;//不知道这个特判有没有用
     while(!q2.empty()) {
         node tmp=q2.front();q2.pop();vis[tmp.x][tmp.y][tmp.k]=;
         if(tmp.x==tx && tmp.y==ty) {//搜到了就停
             ans=min(ans,dist[tmp.x][tmp.y][tmp.k]);
             continue;
         }
         siji(i,,) {
             if(i!=op[tmp.k]) {
                 int nx=tmp.x+dirx[i],ny=tmp.y+diry[i];
                 if(!graph[nx][ny]) continue;
                 int val=wmove[tmp.x][tmp.y][op[tmp.k]][i];
                 if(val<=) continue;//此时说明这个方向格子走不动
                 if(dist[nx][ny][i]>dist[tmp.x][tmp.y][tmp.k]+val+){
                     dist[nx][ny][i]=dist[tmp.x][tmp.y][tmp.k]+val+;
                     if(!vis[nx][ny][i]) {
                         vis[nx][ny][i]=;
                         q2.push((node){nx,ny,i});
                     }
                 }
             }
         }
     }
     if(ans>=inf || ans<) ans=-;
     printf("%d\n",ans);
 }
 void Main() {
     scanf("%d%d%d",&n,&m,&q);
     siji(i,,n) {
         siji(j,,m) {
             scanf("%d",&graph[i][j]);
         }
     }
     siji(i,,n) {
         siji(j,,m) {
             if(graph[i][j]) pre(i,j);
         }
     }
     siji(i,,q) {
         scanf("%d%d%d%d%d%d",&ex,&ey,&sx,&sy,&tx,&ty);
         solve();
     }
 }
 int main() {
     Main();
 }

华容道