bzoj1758Wc10重建计划—

1758: [Wc2010]重建计划

Time Limit: 40 Sec Memory Limit: 162 MB
Submit: 4707 Solved: 1200
[Submit][Status][Discuss]

Description

Input

第一行包含一个正整数N，表示X国的城市个数. 第二行包含两个正整数L和U，表示政策要求的第一期重建方案中修建道路数的上下限接下来的N-1行描述重建小组的原有方案，每行三个正整数Ai,Bi,Vi分别表示道路(Ai,Bi),其价值为Vi 其中城市由1..N进行标号

Output

输出最大平均估值，保留三位小数

Sample Input

4
2 3
1 2 1
1 3 2
1 4 3

Sample Output

2.500

HINT

N<=100000,1<=L<=U<=N-1,Vi<=1000000 新加数据一组 By leoly,但未重测..2016.9.27

　　　　　　　　-by bzoj

https://www.lydsy.com/JudgeOnline/problem.php?id=1758

省选R1虽有些不足之处（D2T1写炸了，还被卡了一个点的常数），不过基于我那点NOIP分，能苟到这个排名就不错了，知足吧~~，（SD一直到前50之前都没有NOIP比我低的......）

于是就来准备R2啦~~

被大佬安利了一发长链剖分

于是就上网找BZOJ的长链剖分题

于是就找到了这个

一看就是分数规划嘛；

套用分数规划的常用二分解法，考虑怎么check，

check需要找条最长链，如果没有[L,U]的限制，可以直接DP最长链（最近怎么光见到这个）

然而有了这个限制DP大概要N^3，（有N^2做法？？N^2log？？）

所以这个限制怎么办呢？

点分加线段树应该可以做（nlog^3）

(点分加单调队列应该可以nlog^2？？)

不过今天要用长链剖分

考虑在每个点X上，维护子树中所有点从根出发到这个点的路径，这样可以通过N^2枚举每两条（深度加起来-二倍X深度）符合范围的路径来各种作差更新答案

N^2枚举所有点，可以改成N^2枚举所有深度，然后可以用一个下标为深度的线段树变成NlogN——因为当两个深度中有一个确定后，另一个的范围是连续的一段区间

然而这个效率总共是N^2log的，也十分不好的

而且内存也开不下，而且维护这个线段树的复杂度也十分不对

后两个问题可以考虑用线段树合并解决，

每个点只有一个深度，所以线段树合并可以做到维护所有点X的时空复杂度为（NlogN）

剩下的问题是NlogN枚举深度进行N次会变为N^2logN

这个怎么办呢？

注意我们对每个X的子树的枚举过程：

——把前i-1个儿子的子树和X合并，然后枚举第i个儿子的子树中的所有深度在X的线段树中查找

这样可以在不遗漏的前提下尽可能少查询

但是，对i=1时不应该这么做，

因为即使枚举第一个儿子的所有深度，所能查到的另一个深度也只有x自己的那一个深度，

所以在i=1时，可以考虑在第一个儿子的线段树中查询一个可以和X自己的深度匹配的区间

但是这样虽然常数可能小一点，但效率还是NlogN的

然而，我们发现，实际上对于每个X而言，都有第一个儿子的对应信息没有枚举！！

理所当然地，我们希望第一个儿子是最大深度最大的那个儿子，这样可以更快些；

可是，对于复杂度而言，这有什么用吗？

其实这对于复杂度而言十分有用：

这时，我们考虑在枚举所有X的子树的过程中，每个点对效率的影响

每个点只会在枚举其祖先的子树时有可能影响效率

我们把这棵树按照子树的最大深度而不是子树大小来剖分

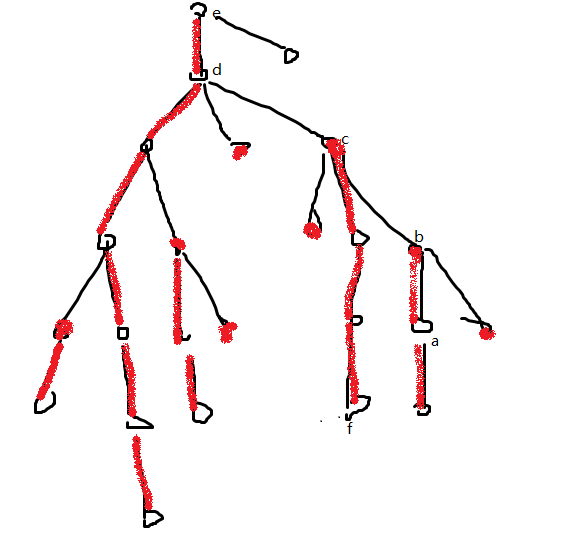
如上图所示
这时我们发现，每个点a只会在枚举到他所在的重链的顶端的父亲时对效率造成log的影响

因为：

在枚举a所在的重链中的其他祖先节点时，a所在的子树都是作为深度最深的那个而没有被枚举（如枚举b的子树时，a所在的子树是最深的，没有被枚举深度）

在枚举更靠上的重链内部时，a所在的子树也是作为深度最深的那个而没有被枚举(如枚举e的子树时，a在d这个子树内，作为最深的存在，没有被枚举深度)

在枚举更靠上的重链顶端的父亲时，虽然a所在的子树需要枚举，但由于我们枚举的是深度，所以因为这个子树有更深的链所以这个效率应该算作那个更深的链的效率（如当枚举d的子树时，尽管a所在的子树被枚举了深度，但这个效率应该被算在cf链上）

所以这个方法可以做到nlogn

这个“按子树最大深度剖分树链，对长链链接的子节点不做操作”的技巧被称作一种长链剖分

于是我们完美地用$Nlog_2^2N$解决了这个问题

(upd 2018.5.24:不采用线段树合并，转而采用基于长链剖分的暴力线段树插入，好像也可以保证效率)

代码：

#include<cstdio>

#include<cstring>

#include<algorithm>

#define LL long long

using namespace std;

const LL exp=;

const LL INF=1e15;

struct ss{

    int to,next;

    LL val;

}e[];

int first[],num;

struct DT{

    LL max;

    int ch[];

}data[];

int root[],tot;

int dep[],depst[],hw[];

LL val[];

LL l,r,mid,ans;

int n,Low,Top;

void build(int ,int ,LL );

bool check(LL );

void dfs_1(int ,int );

void dfs_2(int );

void insert(int ,int ,int&,int ,LL );

LL get_max(int ,int ,int ,int ,int );

LL get_poi_max(int ,int ,int ,int );

void merge(int ,int ,int ,int&);

int main()

{

    int i,j,k,o;

    scanf("%d",&n);

    scanf("%d%d",&Low,&Top);

    for(i=;i<n;i++){

        scanf("%d%d%d",&j,&k,&o);

        build(j,k,o*exp),build(k,j,o*exp);

    }

    dfs_1(,);

    l=exp,r=1e10,mid=(l+r)>>1ll;

    while(l<r-){

        if(check(mid))    l=mid;

        else            r=mid-;

        mid=(l+r)>>1ll;

    }

    for(mid=r;mid>=l;mid--)

        if(check(mid)){

            printf("%.3lf",mid/10000.0);

            return ;

        }

}

void build(int f,int t,LL v){

    e[++num].next=first[f];

    e[num].to=t,e[num].val=v;

    first[f]=num;

}

bool check(LL lim){

    int i;

    memset(root,,sizeof(root)),tot=;

    memset(data,,sizeof(data)),data[].max=-*INF;

    for(i=;i<=num;i++)    e[i].val-=lim;

    ans=-3e10;

    dfs_2();

    for(i=;i<=num;i++)    e[i].val+=lim;

    return ans>=;

}

void dfs_1(int now,int fa){

    int i;

    dep[now]=dep[fa]+;

    depst[now]=dep[now],hw[now]=-;

    for(i=first[now];i;i=e[i].next)

        if(e[i].to!=fa){

            dfs_1(e[i].to,now);

            if(depst[now]<depst[e[i].to])

                depst[now]=depst[e[i].to],hw[now]=i;

        }

}

void dfs_2(int now){

    int i,j;

    if(hw[now]!=-){

        val[e[hw[now]].to]=val[now]+e[hw[now]].val;

        dfs_2(e[hw[now]].to);

        root[now]=root[e[hw[now]].to];

        if(dep[now]+Low<=depst[now]);

            ans=max(ans,get_max(,n,root[now],dep[now]+Low,min(depst[now],dep[now]+Top))-val[now]);

        insert(,n,root[now],dep[now],val[now]);

    }

    else{

        insert(,n,root[now],dep[now],val[now]);

        return ;

    }

    for(i=first[now];i;i=e[i].next)

        if(dep[e[i].to]>dep[now]&&i!=hw[now]){

            val[e[i].to]=val[now]+e[i].val;

            dfs_2(e[i].to);

            for(j=dep[e[i].to];j<=depst[e[i].to]&&j<=dep[now]+Top;j++)

                ans=max(ans,get_poi_max(,n,root[e[i].to],j)-val[now]+get_max(,n,root[now],max(dep[now]*+Low-j,dep[now]+),min(dep[now]*+Top-j,depst[now]))-val[now]);

            merge(,n,root[e[i].to],root[now]);

        }

}

void insert(int l,int r,int&now,int lim,LL x){

    if(!now)now=++tot;

    if(l==r){

        data[now].max=x;

        return ;

    }

    int mid=(l+r)>>;

    if(lim<=mid)

        insert(l,mid,data[now].ch[],lim,x);

    else

        insert(mid+,r,data[now].ch[],lim,x);

    data[now].max=max(data[data[now].ch[]].max,data[data[now].ch[]].max);

}

LL get_max(int l,int r,int now,int L,int R){

    if(L>R)return data[].max;

    if(L<=l&&r<=R)

        return data[now].max;

    int mid=(l+r)>>;

    LL lm=-INF,rm=-INF;

    if(L<=mid)

        lm=get_max(l,mid,data[now].ch[],L,R);

    if(R>mid)

        rm=get_max(mid+,r,data[now].ch[],L,R);

    if(lm>rm)    return lm;

    return rm;

}

LL get_poi_max(int l,int r,int now,int lim){

    if(l==r)return data[now].max;

    int mid=(l+r)>>;

    if(lim<=mid)

        return get_poi_max(l,mid,data[now].ch[],lim);

    else

        return get_poi_max(mid+,r,data[now].ch[],lim);

}

void merge(int l,int r,int pre,int&now){

    if(!now||!pre){

        now+=pre;

        return ;

    }

    if(l==r){

        data[now].max=max(data[now].max,data[pre].max);

        return ;

    }

    int mid=(l+r)>>;

    merge(l,mid,data[pre].ch[],data[now].ch[]);

    merge(mid+,r,data[pre].ch[],data[now].ch[]);

    data[now].max=max(data[data[now].ch[]].max,data[data[now].ch[]].max);

}

（bzoj卡到39S......）