NOIp 2018 普及组

T1标题统计

传送门

题目描述

凯凯刚写了一篇美妙的作文，请问这篇作文的标题中有多少个字符？注意：标题中可能包含大、小写英文字母、数字字符、空格和换行符。统计标题字符数时，空格和换行符不计算在内。

输入输出格式

输入格式：

输入文件只有一行，一个字符串 $ s $ 。

输出格式：

输出文件只有一行，包含一个整数，即作文标题的字符数（不含空格和换行符）。

输入输出样例

输入样例#1：

234

输出样例#1：

3

输入样例#2：

Ca 45

输出样例#2：

4

说明

【数据规模与约定】

规定 $ |s| $ 表示字符串 $ s $ 的长度（即字符串中的字符和空格数）。

对于 $ %40 $ 的数据，$ 1 ≤ |s| ≤ 5 $ ，保证输入为数字字符及行末换行符。

对于 $ %80 $ 的数据，$ 1 ≤ |s| ≤ 5 $ ，输入只可能包含大、小写英文字母、数字字符及行末换行符。

对于 $ %100% $ 的数据，$ 1 ≤ |s| ≤ 5 $ ，输入可能包含大、小写英文字母、数字字符、空格和行末换行符。

这个题感觉大水题吧，会用 $ gets $ 输入感觉问题就不大。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <map>
#include <set>
#define re register
using namespace std ;
char s[10] ;
int ans , len ;
int main() {
	gets(s) ;
	len = strlen(s);
	for(re int i = 0 ; i < len ; ++i) {
		if(s[i] >= '0' && s[i] <= '9')  ans ++ ;
		if(s[i] >= 'A' && s[i] <= 'Z')  ans ++ ;
		if(s[i] >= 'a' && s[i] <= 'z')  ans ++ ;
	}
	printf("%d\n" , ans) ;
	return 0 ;
}

T2龙虎斗

传送门啦

题目描述

轩轩和凯凯正在玩一款叫《龙虎斗》的游戏，游戏的棋盘是一条线段，线段上有 $ n $ 个兵营（自左至右编号 $ 1 \sim n $ ），相邻编号的兵营之间相隔 $ 1 $ 厘米，即棋盘为长度为 $ n-1 $ 厘米的线段。$ i $ 号兵营里有 $ c[i] $ 位工兵。

下面图 1 为 $ n=6 $ 的示例：

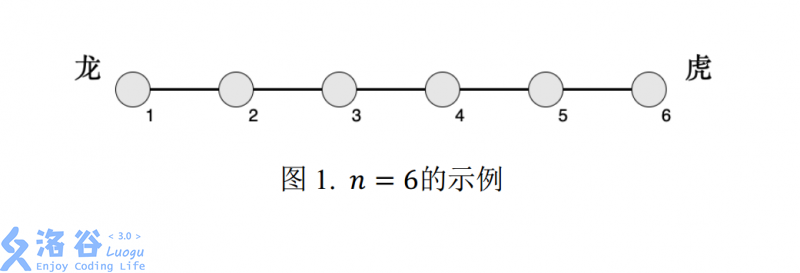
轩轩在左侧，代表“龙”；凯凯在右侧，代表“虎”。他们以 $ m $ 号兵营作为分界，靠左的工兵属于龙势力，靠右的工兵属于虎势力，而第 $ m $ 号兵营中的工兵很纠结，他们不属于任何一方。

一个兵营的气势为：该兵营中的工兵数 $ \times $ 该兵营到 $ m $ 号兵营的距离；参与游戏一方的势力定义为：属于这一方所有兵营的气势之和。

下面图 2 为 $ n = 6,m = 4 $ 的示例，其中红色为龙方，黄色为虎方：

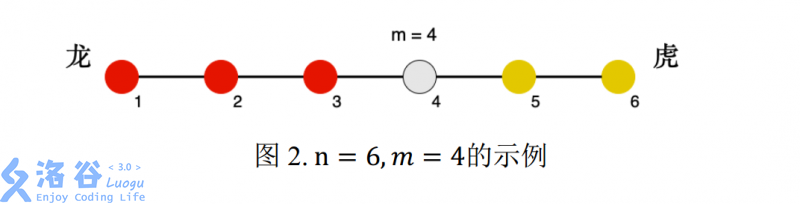
游戏过程中，某一刻天降神兵，共有 $ s_1 $ 位工兵突然出现在了 $ p_1 $ 号兵营。作为轩轩和凯凯的朋友，你知道如果龙虎双方气势差距太悬殊，轩轩和凯凯就不愿意继续玩下去了。为了让游戏继续，你需要选择一个兵营 $ p_2 $ ，并将你手里的 $ s_2 $ 位工兵全部派往兵营 $ p_2 $ ，使得双方气势差距尽可能小。

注意：你手中的工兵落在哪个兵营，就和该兵营中其他工兵有相同的势力归属（如果落在 $ m $ 号兵营，则不属于任何势力）。

输入输出格式

输入格式：

输入文件的第一行包含一个正整数 $ n $ ，代表兵营的数量。

接下来的一行包含 $ n $ 个正整数，相邻两数之间以一个空格分隔，第 $ i $ 个正整数代表编号为 $ i $ 的兵营中起始时的工兵数量 $ c[i] $ 。

接下来的一行包含四个正整数，相邻两数间以一个空格分隔，分别代表 $ m,p_1,s_1,s_2 $ 。

输出格式：

输出文件有一行，包含一个正整数，即 $ p_2 $ ，表示你选择的兵营编号。如果存在多个编号同时满足最优，取最小的编号。

输入输出样例

输入样例#1：

6

2 3 2 3 2 3

4 6 5 2

输出样例#1：

2

输入样例#2：

6

1 1 1 1 1 16

5 4 1 1

输出样例#2：

1

说明

【输入输出样例 1 说明】

见问题描述中的图 2。

双方以 $ m=4 $ 号兵营分界，有 $ s_1=5 $ 位工兵突然出现在 $ p_1=6 $ 号兵营。龙方的气势为：

$ 2 \times (4-1)+3 \times (4-2)+2 \times (4-3) = 142×(4−1)+3×(4−2)+2×(4−3)=14 $

虎方的气势为：

$ 2 \times (5 - 4) + (3 + 5) \times (6 - 4) = 182×(5−4)+(3+5)×(6−4)=18 $

当你将手中的 $ s_2 = 2 $ 位工兵派往 $ p_2 = 2 $ 号兵营时，龙方的气势变为：

$ 14 + 2 \times (4 - 2) = 1814+2×(4−2)=18 $

此时双方气势相等。

【输入输出样例 2 说明】

双方以 $ m = 5 $ 号兵营分界，有 $ s_1 = 1 $ 位工兵突然出现在 $ p_1 = 4 $ 号兵营。

龙方的气势为：

$ 1 \times (5 - 1) + 1 \times (5 - 2) + 1 \times (5 - 3) + (1 + 1) \times (5 - 4) =11 $

虎方的气势为：

$ 16 \times (6 - 5) = 16 $

当你将手中的 $ s_2 = 1 $ 位工兵派往 $ p_2 = 1 $ 号兵营时，龙方的气势变为：

$ 11 + 1 \times (5 - 1) = 15 $

此时可以使双方气势的差距最小。

【数据规模与约定】

$ 1 < m < n,1 ≤ p_1 ≤ n $ 。

对于 $ %20 $ 的数据，$ n = 3,m = 2, c_i = 1, s_1,s_2 ≤ 100 $ 。

另有 $ %20 $ 的数据，$ n ≤ 10, p_1 = m, c_i = 1, s_1,s_2 ≤ 100 $ 。

对于 $ %60 $ 的数据，$ n ≤ 100, c_i = 1, s_1,s_2 ≤ 100 $ 。

对于 $ %80 $ 的数据，$ n ≤ 100, c_i,s_1,s_2 ≤ 100 $ 。

对于 $ %100 $ 的数据， $ n≤10^5

,c_i,s_1,s_2≤10^9 $ 。

分析：

这个题是很纯的模拟题，就是各种符号有点乱，注意不要打错就好了。模拟的时候在每个点上都加上一次试试，不会超时，而且实现更简单，维护一个最小的差。

需要注意的是如果我们加上这些士兵之后比原来的差值还大，那就放 $ m $ 号点上就好了（ $ m $ 点加没加无所谓）

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <map>
#include <queue>
#define re register
using namespace std ;
const int maxn = 1e5 + 3 ;
inline long long read() {
    char ch = getchar();
    long long f = 1 , x = 0;
    while(ch > '9' || ch < '0') { if(ch == '-') f = -1 ; ch = getchar () ;}
    while(ch >= '0' && ch <= '9') { x = (x << 1) + (x << 3 ) + ch - '0' ; ch = getchar() ;}
    return x * f;
}
long long n , c[maxn] , m , p1 , s1 , s2 , p2 ;
long long now1 , now2 ;
int main () {
	//freopen("lhd.in","r",stdin);
	n = read() ;
	for(re int i = 1 ; i <= n ; ++ i) {
		c[i] = read() ;
	}
	m = read() ; p1 = read() ; s1 = read() ; s2 = read() ;
	c[p1] += s1 ;
	for(re int i = 1 ; i <= m - 1 ; ++ i)  now1 += (m - i) * c[i] ;
	for(re int i = m + 1 ; i <= n ; ++ i)  now2 += (i - m) * c[i] ;
	//printf("\n%lld\n%lld\n\n" , now1 , now2) ;
	long long cha = 1e9 ;
	long long f = 0 ;
	if(now1 == now2)  printf("%lld\n" , m) ;
	else if(now1 > now2) {
		for(re int i = m + 1 ; i <= n ; ++ i) {
			if(now2 + (i - m) * s2 == now1) {
				f = i ;
				break ;
			}
			else {
				if(cha > abs(now2 + (i - m) * s2 - now1)) {
					cha = abs(now2 + (i - m) * s2 - now1) ;
					f = i ;
				}
			}
		}
		if(now1 - now2 < cha)  printf("%lld\n" , m) ;
		else printf("%lld\n" , f) ;
	}
	else {
		for(re int i = 1 ; i <= m - 1 ; ++ i) {
			if(now1 + (m - i) * s2 == now2) {
				f = i ;
				break ;
			}
			else {
				if(cha > abs(now1 + (m - i) * s2 - now2)) {
					f = i ;
					cha = abs(now1 + (m - i) * s2 - now2) ;
				}
			}
		}
		if(now2 - now1 < cha)  printf("%lld\n" , m) ;
		else printf("%lld\n" , f) ;
	}
	return 0 ;
}

对称二叉树

传送门

题目描述

一棵有点权的有根树如果满足以下条件，则被轩轩称为对称二叉树：

二叉树；
将这棵树所有节点的左右子树交换，新树和原树对应位置的结构相同且点权相等。

下图中节点内的数字为权值，节点外的 id 表示节点编号。

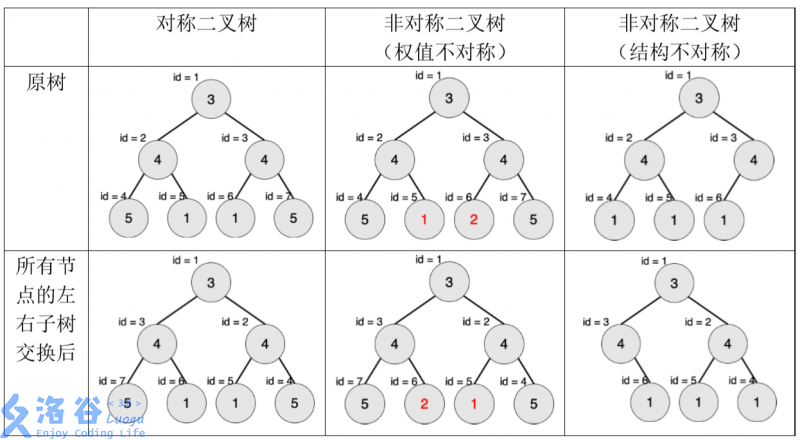
现在给出一棵二叉树，希望你找出它的一棵子树，该子树为对称二叉树，且节点数最多。请输出这棵子树的节点数。

注意：只有树根的树也是对称二叉树。本题中约定，以节点 $ T $ 为子树根的一棵“子树”指的是：节点 $ T $ 和它的全部后代节点构成的二叉树。

输入输出格式

输入格式：

第一行一个正整数 $ n $ ，表示给定的树的节点的数目，规定节点编号 $ 1 \sim n $ ，其中节点 $ 1 $ 是树根。

第二行 $ n $ 个正整数，用一个空格分隔，第 $ i $ 个正整数 $ v_i $ 代表节点 $ i $ 的权值。

接下来 $ n $ 行，每行两个正整数 $ l_i , r_i $ ，分别表示节点 $ i $ 的左右孩子的编号。如果不存在左 / 右孩子，则以 $ -1 $ 表示。两个数之间用一个空格隔开。

输出格式：

输出文件共一行，包含一个整数，表示给定的树的最大对称二叉子树的节点数。

输入输出样例

输入样例#1：

2

1 3

2 -1

-1 -1

输出样例#1：

1

输入样例#2：

10

2 2 5 5 5 5 4 4 2 3

9 10

-1 -1

-1 -1

-1 -1

-1 -1

-1 2

3 4

5 6

-1 -1

7 8

输出样例#2：

3

【数据规模与约定】

共 $ 25 $ 个测试点。 $ v_i ≤ 1000 $ 。

测试点 $ 1 \sim 3, n ≤ 10 $ ，保证根结点的左子树的所有节点都没有右孩子，根结点的右子树的所有节点都没有左孩子。

测试点 $ 4 \sim 8 , n ≤ 10 $ 。

测试点 $ 9 \sim 12, n ≤ 10^5 $ ，保证输入是一棵“满二叉树” 。

测试点 $ 13 \sim 16, n ≤ 10^5 $ ，保证输入是一棵“完全二叉树”。

测试点 $ 17 \sim 20, n ≤ 10^5 $ ，保证输入的树的点权均为 1。

测试点 $ 21 \sim 25, n ≤ 10^6 $ 。

本题约定：

层次：节点的层次从根开始定义起，根为第一层，根的孩子为第二层。树中任一节点的层次等于其父亲节点的层次加 $ 1 $ 。

树的深度：树中节点的最大层次称为树的深度。

满二叉树：设二叉树的深度为 $ h $ ，且二叉树有 $ 2h-1 $ 个节点，这就是满二叉树。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
using namespace std ;
#define re register
const int maxn = 1e6 + 3 ;
inline int read () {
	int f = 1 , x = 0 ;
	char ch = getchar() ;
	while(ch > '9' || ch < '0') {if(ch == '-') f = -1 ; ch = getchar () ;}
	while(ch >= '0' && ch <= '9') {x = (x << 1) + (x << 3) + ch - '0' ; ch = getchar () ;}
	return x * f ;
}
int n , v[maxn] ;
int l[maxn] , r[maxn] ;
int ch[maxn][2] , c[maxn] , ans ;
//c[]记录当前最大的节点数
bool check (int a , int b) {
	//判断两个点是否对称
	if(a == b)  return true ; //同一个点也算对称
	//if(!a || !b)  return false ;
	if(v[a] != v[b])  return false ;  //值不相等不算
	return (check(ch[a][1] , ch[b][2]) && check(ch[a][2] , ch[b][1]) ) ;
}
inline void dfs (int x) {
	if(!x)  return ;
	dfs(ch[x][1]) ;
	dfs(ch[x][2]) ;
	c[x] = 1 + c[ch[x][1]] + c[ch[x][2]] ;
	//该点最大节点数 = 本身 1 + 左儿子的节点数 + 右儿子的节点数 ；
	v[x] = v[x] + v[ch[x][1]] + v[ch[x][2]] ;
	//为了判断（两个子树中的总值不相等也说明不对称）
	if(ans < c[x] && check(ch[x][1] , ch[x][2])) //左右儿子对称
		ans = c[x] ;
}
int main () {
	n = read () ;
	for(re int i = 1 ; i <= n ; ++ i) {
		v[i] = read () ;
	}
	v[0] = 1005 ;
	for(re int i = 1 ; i <= n ; ++ i) {
		l[i] = read () ;
		if(l[i] != -1)	ch[i][1] = l[i] ;
		r[i] = read () ;
		if(r[i] != -1)	ch[i][2] = r[i] ;
	}
	dfs(1) ;
	printf("%d\n" , ans ) ;
	return 0 ;
}