计算几何---凸包问题（Graham/Andrew Scan ）

概念

凸包(Convex Hull)是一个计算几何（图形学）中的概念。用不严谨的话来讲，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边型，它能包含点集中所有点的。严谨的定义和相关概念参见维基百科：凸包。

也被称为：Graham/Andrew Scan 算法。在二维欧几里得空间中，凸包可想象为一条刚好包着所有点的橡皮圈。

问题

给定平面上的二维点集，求解其凸包。

　　

过程

1. 在所有点中选取y坐标最小的一点H，当作基点。如果存在多个点的y坐标都为最小值，则选取x坐标最小的一点。坐标相同的点应排除。然后按照其它各点p和基点构成的向量<H,p>与x轴的夹角进行排序，夹角由大至小进行顺时针扫描，反之则进行逆时针扫描。实现中无需求得夹角，只需根据向量的内积公式求出向量的模即可。以下图为例，基点为H，根据夹角由小至大排序后依次为H，K，C，D，L，F，G，E，I，B，A，J。下面进行逆时针扫描。

2. 线段<H, K>一定在凸包上，接着加入C。假设线段<K, C>也在凸包上，因为就H，K，C三点而言，它们的凸包就是由此三点所组成。但是接下来加入D时会发现，线段<K, D>才会在凸包上，所以将线段<K, C>排除，C点不可能是凸包。

3. 即当加入一点时，必须考虑到前面的线段是否会出现在凸包上。从基点开始，凸包上每条相临的线段的旋转方向应该一致，并与扫描的方向相反。如果发现新加的点使得新线段与上线段的旋转方向发生变化，则可判定上一点必然不在凸包上。实现时可用向量叉积进行判断，设新加入的点为p_{n + 1}，上一点为p_n，再上一点为p_{n - 1}。顺时针扫描时，如果向量<p_{n - 1}, p_n>与<p_n, p_{n + 1}>的叉积为正（逆时针扫描判断是否为负），则将上一点删除。删除过程需要回溯，将之前所有叉积符号相反的点都删除，然后将新点加入凸包。

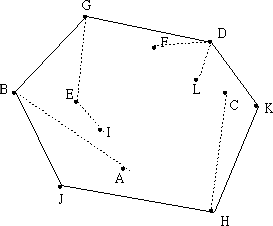
在上图中，加入K点时，由于线段<H,K>相对于<H,C>为顺时针旋转，所以C点不在凸包上，应该删除，保留K点。接着加入D点，由于线段<K, D>相对<H, K>为逆时针旋转，故D点保留。按照上述步骤进行扫描，直到点集中所有的点都遍例完成，即得到凸包。

复杂度

这个算法可以直接在原数据上进行运算，因此空间复杂度为O(1)。但如果将凸包的结果存储到另一数组中，则可能在代码级别进行优化。由于在扫描凸包前要进行排序，因此时间复杂度至少为快速排序的O(nlgn)。后面的扫描过程复杂度为O(n)，因此整个算法的复杂度为O(nlgn)。

代码实现（C++&STL）

 #include <algorithm>
 #include <iostream>
 #include <vector>
 #include <math.h>
 using namespace std;
 //二维点(或向量)结构体定义
 #ifndef _WINDEF_
 struct POINT { int x; int y; };
 #endif
 typedef vector<POINT> PTARRAY;
 //判断两个点(或向量)是否相等
 bool operator==(const POINT &pt1, const POINT &pt2) {
     return (pt1.x == pt2.x && pt1.y == pt2.y);
 }
 // 比较两个向量pt1和pt2分别与x轴向量(1, 0)的夹角
 bool CompareVector(const POINT &pt1, const POINT &pt2) {
     //求向量的模
     float m1 = sqrt((float)(pt1.x * pt1.x + pt1.y * pt1.y));
     float m2 = sqrt((float)(pt2.x * pt2.x + pt2.y * pt2.y));
     //两个向量分别与(1, 0)求内积
     float v1 = pt1.x / m1, v2 = pt2.x / m2;
     return (v1 > v2 || (v1 == v2 && m1 < m2));
 }
 //计算凸包
 void CalcConvexHull(PTARRAY &vecSrc) {
     //点集中至少应有3个点，才能构成多边形
     if (vecSrc.size() < ) {
         return;
     }
     //查找基点
     POINT ptBase = vecSrc.front(); //将第1个点预设为最小点
     for (PTARRAY::iterator i = vecSrc.begin() + ; i != vecSrc.end(); ++i) {
         //如果当前点的y值小于最小点，或y值相等，x值较小
         if (i->y < ptBase.y || (i->y == ptBase.y && i->x > ptBase.x)) {
             //将当前点作为最小点
             ptBase = *i;
         }
     }
     //计算出各点与基点构成的向量
     for (PTARRAY::iterator i = vecSrc.begin(); i != vecSrc.end();) {
         //排除与基点相同的点，避免后面的排序计算中出现除0错误
         if (*i == ptBase) {
             i = vecSrc.erase(i);
         }
         else {
             //方向由基点到目标点
             i->x -= ptBase.x, i->y -= ptBase.y;
             ++i;
         }
     }
     //按各向量与横坐标之间的夹角排序
     sort(vecSrc.begin(), vecSrc.end(), &CompareVector);
     //删除相同的向量
     vecSrc.erase(unique(vecSrc.begin(), vecSrc.end()), vecSrc.end());
     //计算得到首尾依次相联的向量
     for (PTARRAY::reverse_iterator ri = vecSrc.rbegin();
         ri != vecSrc.rend() - ; ++ri) {
         PTARRAY::reverse_iterator riNext = ri + ;
         //向量三角形计算公式
         ri->x -= riNext->x, ri->y -= riNext->y;
     }
     //依次删除不在凸包上的向量
     for (PTARRAY::iterator i = vecSrc.begin() + ; i != vecSrc.end(); ++i) {
         //回溯删除旋转方向相反的向量，使用外积判断旋转方向
         for (PTARRAY::iterator iLast = i - ; iLast != vecSrc.begin();) {
             int v1 = i->x * iLast->y, v2 = i->y * iLast->x;
             //如果叉积小于0，则无没有逆向旋转
             //如果叉积等于0，还需判断方向是否相逆
             if (v1 < v2 || (v1 == v2 && i->x * iLast->x >  &&
                 i->y * iLast->y > )) {
                     break;
             }
             //删除前一个向量后，需更新当前向量，与前面的向量首尾相连
             //向量三角形计算公式
             i->x += iLast->x, i->y += iLast->y;
             iLast = (i = vecSrc.erase(iLast)) - ;
         }
     }
     //将所有首尾相连的向量依次累加，换算成坐标
     vecSrc.front().x += ptBase.x, vecSrc.front().y += ptBase.y;
     for (PTARRAY::iterator i = vecSrc.begin() + ; i != vecSrc.end(); ++i) {
         i->x += (i - )->x, i->y += (i - )->y;
     }
     //添加基点，全部的凸包计算完成
     vecSrc.push_back(ptBase);
 }

 int main(void) {
     int nPtCnt = ; //生成的随机点数
     PTARRAY vecSrc, vecCH;
     for (int i = ; i < nPtCnt; ++i) {
         POINT ptIn = { rand() % , rand() %  };
         vecSrc.push_back(ptIn);
         cout << ptIn.x << ", " << ptIn.y << endl;
     }
     CalcConvexHull(vecSrc);
     cout << "\nConvex Hull:\n";
     for (PTARRAY::iterator i = vecSrc.begin(); i != vecSrc.end(); ++i) {
         cout << i->x << ", " << i->y << endl;
     }
     return ;
 }

参考博客： http://www.cnblogs.com/devymex/archive/2010/08/09/1795392.html

endl;