CS229 1 .线性回归与特征归一化(feature scaling)

线性回归是一种回归分析技术，回归分析本质上就是一个函数估计的问题（函数估计包括参数估计和非参数估计），就是找出因变量和自变量之间的因果关系。回归分析的因变量是应该是连续变量，若因变量为离散变量，则问题转化为分类问题，回归分析是一个有监督学习问题。

线性其实就是一系列一次特征的线性组合，在二维空间中是一条直线，在三维空间中是一个平面，然后推广到n维空间，可以理解维广义线性吧。

例如对房屋的价格预测，首先提取特征，特征的选取会影响模型的精度，比如房屋的高度与房屋的面积，毫无疑问面积是影响房价的重要因素，二高度基本与房价不相关

下图中挑选了 面积、我是数量、层数、建成时间四个特征，然后选取了一些train Set{x⁽ⁱ⁾ , y⁽ⁱ⁾}。

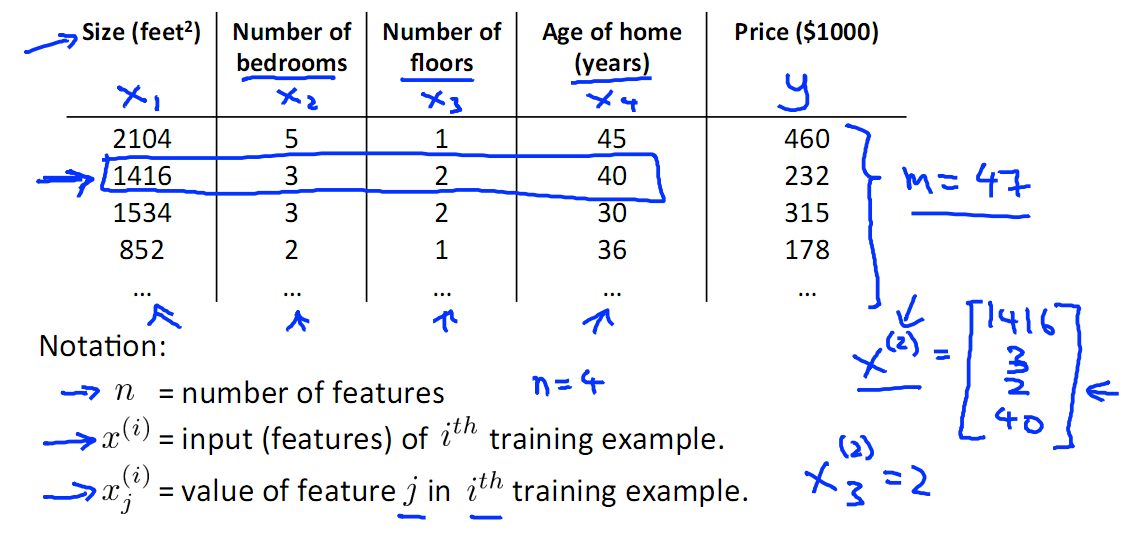
有了这些数据之后就是进行训练，下面附一张有监督学习的示意图

Train Set 根据 学习算法得到模型h，对New Data x，直接用模型即可得到预测值y，本例中即可得到房屋大小，其实本质上就是根据历史数据来发现规律，事情总是偏向于向历史发生过次数多的方向发展。

下面就是计算模型了，才去的措施是经验风险最小化，即我们训练模型的宗旨是，模型训练数据上产生结果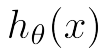, 要与实际的y⁽ⁱ⁾越接近越好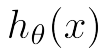（假定x₀ =1），定义损失函数J(θ)如下,即我们需要损失函数越小越好，本方法定义的J(θ)在最优化理论中称为凸（Convex）函数，即全局只有一个最优解，然后通过梯度下降算法找到最优解即可，梯度下降的形式已经给出。

梯度下降的具体形式：关于梯度下降的细节，请参阅 梯度下降详解

局部加权回归

有时候样本的波动很明显，可以采用局部加权回归，如下图，红色的线为局部加权回归的结果，蓝色的线为普通的多项式回归的结果。蓝色的线有一些欠拟合了。

局部加权回归的方法如下，首先看线性或多项式回归的损失函数“

很明显，局部加权回归在每一次预测新样本时都会重新确定参数，以达到更好的预测效果。当数据规模比较大的时候计算量很大，学习效率很低。并且局部加权回归也不是一定就是避免underfitting，因为那些波动的样本可能是异常值或者数据噪声。

在求解线性回归的模型时，有两个需要注意的问题

一就是特征组合问题，比如房子的长和宽作为两个特征参与模型的构造，不如把其相乘得到面积然后作为一个特征来进行求解，这样在特征选择上就做了减少维度的工作。

二就是特征归一化（Feature Scaling），这也是许多机器学习模型都需要注意的问题。

有些模型在各个维度进行不均匀伸缩后，最优解与原来不等价，例如SVM。对于这样的模型，除非本来各维数据的分布范围就比较接近，否则必须进行标准化，以免模型参数被分布范围较大或较小的数据dominate。

有些模型在各个维度进行不均匀伸缩后，最优解与原来等价，例如logistic regression。对于这样的模型，是否标准化理论上不会改变最优解。但是，由于实际求解往往使用迭代算法，如果目标函数的形状太“扁”，迭代算法可能收敛得很慢甚至不收敛。所以对于具有伸缩不变性的模型，最好也进行数据标准化。

归一化后有两个好处：

1. 提升模型的收敛速度

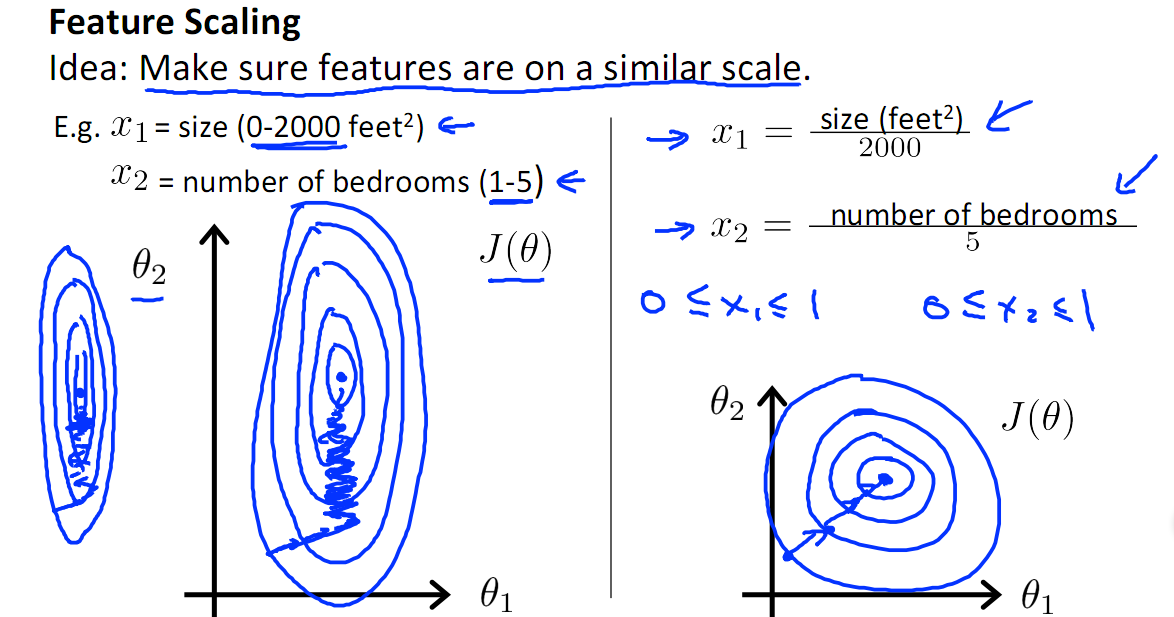
如下图，x₁的取值为0-2000，而x₂的取值为1-5，假如只有这两个特征，对其进行优化时，会得到一个窄长的椭圆形，导致在梯度下降时，梯度的方向为垂直等高线的方向而走之字形路线，这样会使迭代很慢，相比之下，右图的迭代就会很快

2.提升模型的精度

归一化的另一好处是提高精度，这在涉及到一些距离计算的算法时效果显著，比如算法要计算欧氏距离，上图中x2的取值范围比较小，涉及到距离计算时其对结果的影响远比x1带来的小，所以这就会造成精度的损失。所以归一化很有必要，他可以让各个特征对结果做出的贡献相同。

下边是常用归一化方法

1）. 线性归一化，线性归一化会把输入数据都转换到[0 1]的范围，公式如下

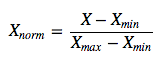
该方法实现对原始数据的等比例缩放，其中Xnorm为归一化后的数据，X为原始数据，Xmax、Xmin分别为原始数据集的最大值和最小值。

2）. 0均值标准化，0均值归一化方法将原始数据集归一化为均值为0、方差1的数据集，归一化公式如下：

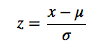
其中，μ、σ分别为原始数据集的均值和方法。该种归一化方式要求原始数据的分布可以近似为高斯分布，否则归一化的效果会变得很糟糕。

关于归一化方法的选择

1） 在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，第二种方法(Z-score standardization)表现更好。

2） 在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用第一种方法或其他归一化方法。比如图像处理中，将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。

选择方法是参考自http://blog.csdn.net/zbc1090549839/article/details/44103801，至于为什么，我现在也还不清楚

线性回归，我用java实现的，源码地址 https://github.com/ooon/toylib

参考文献：

http://www.cnblogs.com/LBSer/p/4440590.html