三个理论上界：

三个线性模型：

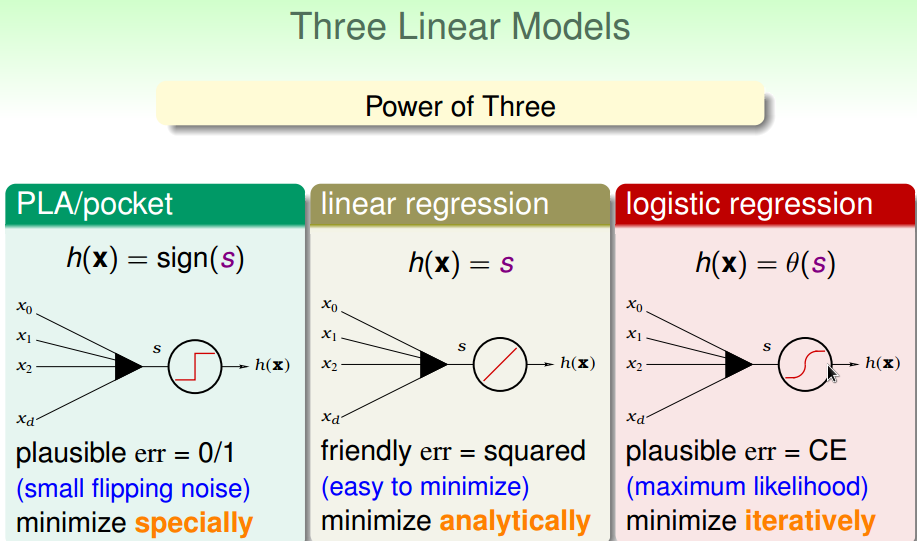
三个关键工具：

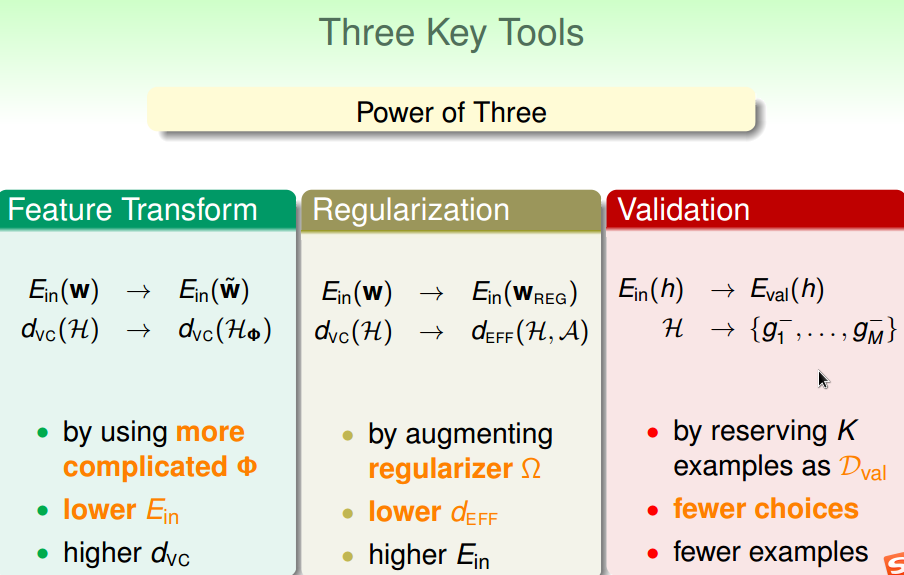
三条学习规则：

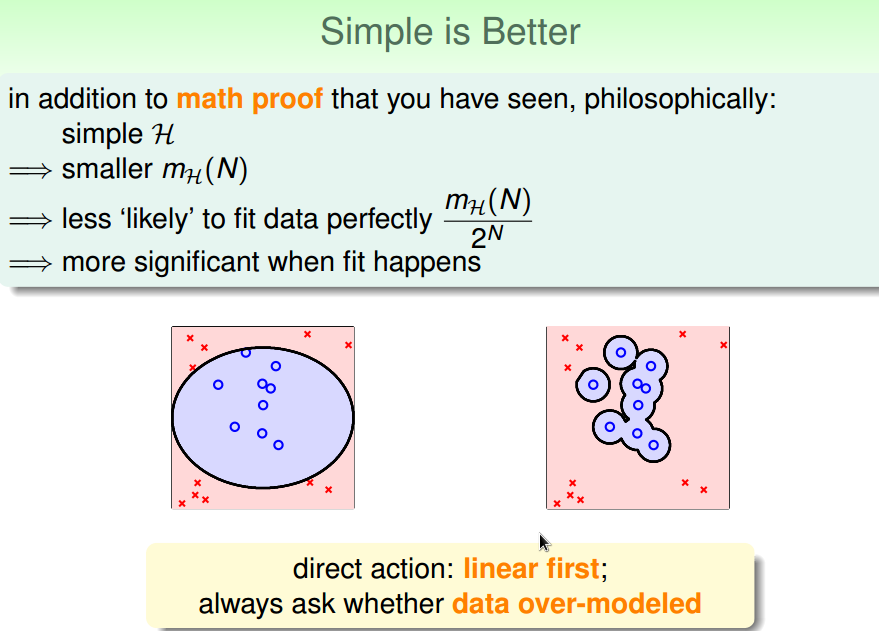
1.奥卡姆剃刀定律

先从简单模型开始,

训练后出现欠拟合,

再尝试复杂点模型。

2.采样误差

训练、验证、测试数据尽量同分布。

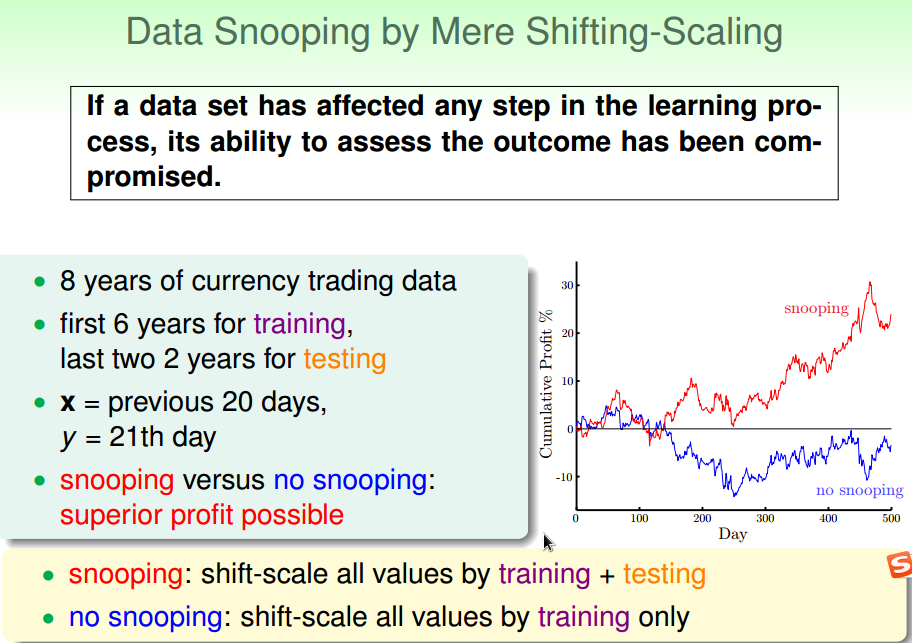
3.数据偷看

找到折中方法。

机器学习基石笔记：16 Three Learning Principles的更多相关文章

  1. 机器学习基石：16 Three Learning Principles

    三个理论上界: 三个线性模型: 三个关键工具: 三条学习规则: 1.奥卡姆剃刀定律 先从简单模型开始, 训练后出现欠拟合, 再尝试复杂点模型. 2.采样误差 训练.验证.测试数据尽量同分布. 3.数据 ...

  2. Coursera台大机器学习课程笔记15 -- Three Learning Principles

    这节课是最后一节,讲的是做机器学习的三个原则. 第一个是Occan's razor,即越简单越好.接着解释了什么是简单的hypothesis,什么是简单的model.关于为什么越简单越好,林老师从大致 ...

  3. 林轩田机器学习基石笔记1—The Learning Problem

    机器学习分为四步: When Can Machine Learn? Why Can Machine Learn? How Can Machine Learn? How Can Machine Lear ...

  4. 机器学习基石笔记：02 Learning to Answer Yes/No、PLA、PA

    原文地址:https://www.jianshu.com/p/ed0aee74523f 一.Perceptron Learning Algorithm (一)算法原理 PLA本质是二元线性分类算法,即 ...

  5. 机器学习基石 4 Feasibility of Learning

    机器学习基石 4 Feasibility of Learning Learning is Impossible? 机器学习:通过现有的训练集 \(D\) 学习,得到预测函数 \(h(x)\) 使得它接 ...

  6. 机器学习基石 3 Types of Learning

    机器学习基石 3 Types of Learning Learning with Different Output Space Learning with Different Data Label L ...

  7. 机器学习基石笔记：01 The Learning Problem

    原文地址:https://www.jianshu.com/p/bd7cb6c78e5e 什么时候适合用机器学习算法? 存在某种规则/模式,能够使性能提升,比如准确率: 这种规则难以程序化定义,人难以给 ...

  8. 林轩田机器学习基石笔记4—Feasibility of Learning

    上节课介绍了机器学习可以分为不同的类型.其中,监督式学习中的二元分类和回归分析是最常见的也是最重要的机器学习问题.本节课,我们将介绍机器学习的可行性,讨论问题是否可以使用机器学习来解决. 一.Lear ...

  9. 林轩田机器学习基石笔记3—Types of Learning

    上节课我们主要介绍了解决线性分类问题的一个简单的方法:PLA.PLA能够在平面中选择一条直线将样本数据完全正确分类.而对于线性不可分的情况,可以使用Pocket Algorithm来处理.本节课将主要 ...

随机推荐

  1. AOP （切点表达式讲解）

    Spring EL表达式:: 1.execution 表达式 语法格式: execution(返回类型.包名.类名.方法名(参数表)) exection(*.com.xxx.AService.*(.. ...

  2. php 超时设置笔记

    php.ini default_socket_timeout=5 mysql.connect_timeout = 5 max_execution_time = 5 php-fpm pm = dynam ...

  3. floor函数

    C++中 可以用floor函数来截断小数部分 floor(x)返回一个不大于x的整数,有点像取整函数

  4. 2019.01.04 bzoj2962: 序列操作（线段树+组合数学）

    传送门 线段树基础题. 题意:要求维护区间区间中选择ccc个数相乘的所有方案的和(c≤20c\le20c≤20),支持区间加,区间取负. 由于c≤20c\le20c≤20,因此可以对于每个线段树节点可 ...

  5. Le Chapitre I

    Lorsque j'avais six ans j'ai vu, une fois, une magnifique image, dans un livre sur la Forêt[fɔrε] Vi ...

  6. DevExpress 只允许修改指定列

    gridView1.OptionsBehavior.Editable = true; gridView1.OptionsBehavior.ReadOnly = false; foreach (Grid ...

  7. rm与管道使用

    一 问题初始:用通常意义的管道使用这样可以:(1)ls -l | sed -n '/~$/p' 我用显示出系统自己建立的备份文件这时,我想删除这些文件,我仍然使用了管道,并执行了以下命令(2)ls - ...

  8. Eclipse的maven项目一直无故报错

    maven项目里面没报错,就是项目名称上有红色的叉叉,看着很不舒服: install都成功,但还是有红叉,刷新也没有用,最后搞了好一会才好: 操作步骤: 1.先把项目clean下: 选中要清理的项目, ...

  9. java并发里的一些基础概念

    转载自:https://my.oschina.net/hosee/blog/597934: 摘要: 本系列基于炼数成金课程,为了更好的学习,做了系列的记录. 本文主要介绍 1.高并发的概念,为以后系列 ...

  10. noip第2课作业

    1.    大象喝水 [问题描述] 一只大象口渴了,要喝20升水才能解渴,但现在只有一个深h厘米,底面半径为r厘米的小圆桶(h和r都是整数).问大象至少要喝多少桶水才会解渴. 输入:输入有一行,包行两 ...