吴恩达《深度学习》-课后测验-第一门课 (Neural Networks and Deep Learning)-Week 3 - Shallow Neural Networks（第三周测验 - 浅层神 经网络）

Week 3 Quiz - Shallow Neural Networks（第三周测验 - 浅层神经网络）

\1. Which of the following are true? (Check all that apply.) Notice that I only list correct options(以下哪一项是正确的？只列出了正确的答案)

【 】 is a matrix in which each column is one training example.(是一个矩阵，其中每个列都 是一个训练样本。)

【 】\(_4^{[2]}\) is the activation output by the 4th neuron of the 2nd layer(4 [2]是第二层第四层神经 元的激活的输出。)

【 】\(^{[2](12)}\) denotes the activation vector of the 2nd layer for the 12th training example.(表\(^{[2](12)}\)示第二层和第十二层的激活向量。)

【 】\(^{[2]}\) denotes the activation vector of the 2nd layer.(\(^{[2]}\) 表示第二层的激活向量。)

答案

全对

\2. The tanh activation usually works better than sigmoid activation function for hidden units because the mean of its output is closer to zero, and so it centers the data better for the next layer. True/False?(tanh 激活函数通常比隐藏层单元的 sigmoid 激活函数效果更好，因为其 输出的平均值更接近于零，因此它将数据集中在下一层是更好的选择，请问正确吗？)

【 】True(正确) 【 】 False(错误)

答案

True

Note: You can check this post and(this paper)(请注意，你可以看一下这篇文章 和这篇文档.)

As seen in lecture the output of the tanh is between -1 and 1, it thus centers the data which makes the learning simpler for the next layer.(tanh 的输出在-1 和 1 之间，因此它将数据集中在一起，使得下 一层的学习变得更加简单。)

\3. Which of these is a correct vectorized implementation of forward propagation for layer , where ≤ ≤ ? Notice that I only list correct options(其中哪一个是第 l 层向前传播的正确 向量化实现，其中 ≤ ≤ )(以下哪一项是正确的？只列出了正确的答案)

【 】$^{[]} = ^{[]}{[−1]} + ^{[]} $

【 】\(^{[]} = ^{[]} (^{[]} )\)

答案

全对

\4. You are building a binary classifier for recognizing cucumbers (y=1) vs. watermelons (y=0). Which one of these activation functions would you recommend using for the output layer?(您 正在构建一个识别黄瓜（y = 1）与西瓜（y = 0）的二元分类器。 你会推荐哪一种激活函数 用于输出层？)

【 】 ReLU 【 】 Leaky ReLU 11 【 】 sigmoid 【 】 tanh

答案

sigmoid

Note: The output value from a sigmoid function can be easily understood as a probability.(注意：来自 sigmoid 函数的输出值可以很容易地理解为概率。)

Sigmoid outputs a value between 0 and 1 which makes it a very good choice for binary classification.You can classify as 0 if the output is less than 0.5 and classify as 1 if the output is more than 0.5. It can be done with tanh as well but it is less convenient as the output is between -1 and 1. Sigmoid 输出的值介于 0 和 1 之间，这使其成为二元分类的一个非常好的选择。 如果输出小于 0.5，则可以将其归类为 0，如果输出大于 0.5，则归类为 1。 它也可以用 tanh 来完成，但是它不太方便，因为输出在-1 和 1 之间。)

\5. Consider the following code:(看一下下面的代码：)

A = np.random.randn(4,3)
B = np.sum(A, axis = 1, keepdims = True)
What will be B.shape?(请问 B.shape 的值是多少?)

答案

B.shape = (4, 1)

we use (keepdims = True) to make sure that A.shape is (4,1) and not (4, ). It makes our code more rigorous.(我们使用（keepdims = True）来确保 A.shape 是（4,1）而不是（4，），它使 我们的代码更加严格。)

\6. Suppose you have built a neural network. You decide to initialize the weights and biases to be zero. Which of the following statements are True? (Check all that apply)(假设你已经建立 了一个神经网络。 您决定将权重和偏差初始化为零。 以下哪项陈述是正确的？)

【 】Each neuron in the first hidden layer will perform the same computation. So even after multiple iterations of gradient descent each neuron in the layer will be computing the same thing as other neurons.(第一个隐藏层中的每个神经元节点将执行相同的计算。 所以即使经过 多次梯度下降迭代后，层中的每个神经元节点都会计算出与其他神经元节点相同的东西。)

【 】Each neuron in the first hidden layer will perform the same computation in the first iteration. But after one iteration of gradient descent they will learn to compute different things because we have “broken symmetry”.( 第一个隐藏层中的每个神经元将在第一次迭代中执行相 同的计算。 但经过一次梯度下降迭代后，他们将学会计算不同的东西，因为我们已经“破坏了 对称性”。)

【 】Each neuron in the first hidden layer will compute the same thing, but neurons in different layers will compute different things, thus we have accomplished “symmetry breaking” as described in lecture.(第一个隐藏层中的每一个神经元都会计算出相同的东西，但是不同层的神 经元会计算不同的东西，因此我们已经完成了“对称破坏”。)

【 】The first hidden layer’s neurons will perform different computations from each other even in the first iteration; their parameters will thus keep evolving in their own way.(即使在第一次迭 代中，第一个隐藏层的神经元也会执行不同的计算， 他们的参数将以自己的方式不断发展。)

答案

【★】Each neuron in the first hidden layer will perform the same computation. So even after multiple iterations of gradient descent each neuron in the layer will be computing the same thing as other neurons.(第一个隐藏层中的每个神经元节点将执行相同的计算。 所以即使经过 多次梯度下降迭代后，层中的每个神经元节点都会计算出与其他神经元节点相同的东西。)

\7. Logistic regression’s weights w should be initialized randomly rather than to all zeros, because if you initialize to all zeros, then logistic regression will fail to learn a useful decision boundary because it will fail to “break symmetry”, True/False?(Logistic 回归的权重 w 应该随 机初始化，而不是全零，因为如果初始化为全零，那么逻辑回归将无法学习到有用的决策边 界，因为它将无法“破坏对称性”，是正确的吗？)

【 】True(正确) 【 】 False(错误)

答案

False

Note: Logistic Regression doesn’t have a hidden layer. If you initialize the weights to zeros, the first example x fed in the logistic regression will output zero but the derivatives of the Logistic Regression depend on the input x (because there’s no hidden layer) which is not zero. So at the second iteration, the weights values follow x’s distribution and are different from each other if x is not a constant vector.(Logistic 回归没有隐藏层。 如果将权重初始化为零，则 Logistic 回归中的第一个样本 x 将输 出零，但 Logistic 回归的导数取决于不是零的输入 x（因为没有隐藏层）。 因此，在第二次迭代 中，如果 x 不是常量向量，则权值遵循 x 的分布并且彼此不同。)

\8. You have built a network using the tanh activation for all the hidden units. You initialize the weights to relative large values, using np.random.randn(..,..)1000. What will happen?(您已经 为所有隐藏单元使用 tanh 激活建立了一个网络。 使用 np.random.randn（..，..） 1000 将 权重初始化为相对较大的值。 会发生什么？)

【 】 It doesn’t matter. So long as you initialize the weights randomly gradient descent is not affected by whether the weights are large or small.(这没关系。只要随机初始化权重，梯度下降 不受权重大小的影响。)

【 】 This will cause the inputs of the tanh to also be very large, thus causing gradients to also become large. You therefore have to set \(\alpha\) to be very small to prevent divergence; this will slow down learning.(这将导致 tanh 的输入也非常大，因此导致梯度也变大。因此，您必须将 α 设 置得非常小以防止发散; 这会减慢学习速度。)

【 】 This will cause the inputs of the tanh to also be very large, causing the units to be “highly activated” and thus speed up learning compared to if the weights had to start from small values.(这会导致 tanh 的输入也非常大，导致单位被“高度激活”，从而加快了学习速度，而权重必须从小数值开始。)

【 】 This will cause the inputs of the tanh to also be very large, thus causing gradients to be close to zero. The optimization algorithm will thus become slow.(这将导致 tanh 的输入也很 大，因此导致梯度接近于零， 优化算法将因此变得缓慢。)

答案

【★】 This will cause the inputs of the tanh to also be very large, thus causing gradients to be close to zero. The optimization algorithm will thus become slow.(这将导致 tanh 的输入也很大，因此导致梯度接近于零， 优化算法将因此变得缓慢。)

Note:tanh becomes flat for large values, this leads its gradient to be close to zero. This slows down the optimization algorithm.(注：tanh 对于较大的值变得平坦，这导致其梯度接近于零。 这减慢了 优化算法。)

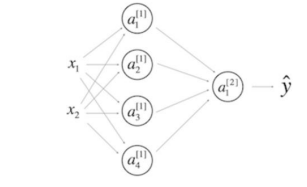
\9. Consider the following 1 hidden layer neural network:(看一下下面的单隐层神经网络)

【 】\(^{[1]}\) will have shape (4, 1)(\(^{[1]}\)的维度是(4, 1))

【 】\(^{[1]}\) will have shape (4, 2)(\(^{[1]}\)的维度是 (4, 2))

【 】\(^{[2]}\) will have shape (1, 4)(\(^{[2]}\) 的维度是 (1, 4))

【 】\(^{[2]}\) will have shape (1, 1)(\(^{[2]}\)的维度是 (1, 1))

答案

全对

Note: Check here for general formulas to do this.(注:来看一下公式)

\10. In the same network as the previous question, what are the dimensions of \(^{[]}\) and \(^{[]}\) ?(在 和上一个相同的网络中，\(^{[]}\) 和 \(^{[]}\)的维度是多少？)

答案

【★】维度都是 (4,m))

---

---

Week 3 Code Assignments：

✧Course 1 - 神经网络和深度学习 - 第三周测验 - 浅层神经网络

✦assignment3：Planar data classification with one hidden layer)