N皇后问题的二进制优化详细思路

题目啊常规解法(DFS)在此就不赘述了。。。

直接进入正题。

　　众所周知，N皇后是NP完全类问题，n稍微大了点求解过程就会变得很长。

算法方面很难再有质的效率突破，但这不妨在其他细节上下下功夫。

　　揆诸常规解法，采用了数组来做mark,以行为每一层进行回溯算法，每个操作周期中无非就做了下面这些事情：

更新元素

判定元素

做出反应

　　更新元素这上面基本上想不到能有啥提升空间了（一次更新多个？？似乎更加复杂了不谈不谈）。。。

做出反应嘛也同样没啥可以进步的地方（做出预判类反应？？也复杂了，不谈不谈）。。。

很显然，有提升空间的就是判定元素环节了。

　　首先，从存储上考虑：

我们采用了三个数组来分别mark两个斜线和一列的占用情况（这里用"占用情况"表示此处是否能落子，如果被‘占用了’，则不能放棋子）

可不可以并成一个数组呢？那么这一个数组就要能够表示三个信息:当前位置一列两斜线的占用情况。有时即使能表示了，但是当移动到下一个位置的时候又得获得新的信息。。似乎不可行。

　　（于是我们又开始无聊地在纸上模拟算法过程了。。。。）

　　诶，然后就会发现，当进行DFS的时候，比如进行到第k层，放下了一个棋子，然后我们就要到下面一层去继续判定，此刻我们用到的信息是第k+1层的占用情况,而k+1的占用情况受到第k层情况的直接影响，如下图：

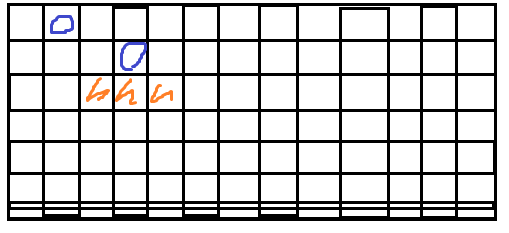
我们会发现第三层涂色的三个位置就不能放棋子了，

　　而除了第k层的影响，前k-1层也对第k+1层有着制约:

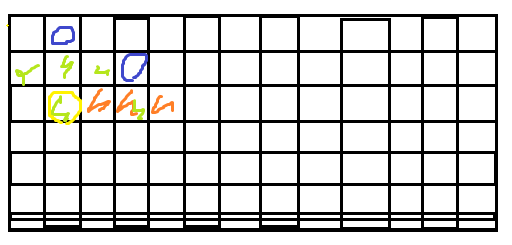
　　再回来看经典算法，每一次标记直接就否定了一条线上的位置，我们跳出这个思维，可不可以“步步为营”，进入到下一行的同时更新出下一行的占用信息？如果这样的话，一个数组足矣。　　

　　再思考，都已经一个数组了（相当于一串数字），而且每个格子就两个状态：有棋子，没棋子。

　　　　显然，二进制是不二选择！而且二进制运算的效率比较高！

　　大概的思路出来了，还有最后一个难点，就是前k-1层的占用信息如何安全过度到第k+1行。。

　　动手尝试了就不难发现这个规律：一个棋子会产生三种影响效果，斜向影响的，到下一层“占用”会斜向相应的方向偏移一格；垂直影响的，到下一层“占用”依旧在相应位置。

如图：

　　这时候就出现了三种类型的信息更新，一串二进制就难以实现了。。。那就三串呗，比起数组仍然不亏了。

　　大的逻辑疙瘩在脑子里基本上解开了，下面开始改代码:

　　首先，咱不用数组，改成int就够了。其次，考虑到每次信息更新的特点，我们可以用函数的形参来传递，省的搞个全局变量让人不爽。

　　函数头这亚子：

void Dfs(int i,int left,int col,int right)//分别是 层数  反斜杠mark  一列mark  斜杠mark 

然后仍然是一般DFS解法的框架，只需要把其中用bool数组mark判断的地方用二进制方法进行替换即可。

放代码：

 void Dfs(int i,int left,int col,int right)//分别是 层数  反斜杠mark  一列mark  斜杠mark
 {
     if (i > N)              //判断是否已经枚举完了N行
     {
         showOneSolution();  //枚举完了就输出（此刻我们处于N+1行）
         return;             //返回到第N行
     }
     for (int j = N-; j >=; --j) //为啥J倒过来数呢？方便下面if中的偏移判断
     {
         if (!(((left|col|right)>>j)&))//(自己解读，有助于提升能力 (好吧我懒）)
         {
             ans[i] = N-j;
             Dfs(i + ,(left|(<<j))<<,(col|(<<j)),(right|(<<j))>>);  //更新“占用信息”的工作就放在参数传递这里了
                                               //这样子的好处就是，回溯的时候不用做什么恢复处理，
                                               //因为这一层的东西基本没变动
         }
     }
 }

这么多括号嵌套的。。哎呀我知道这可读性差，不提倡不提倡！

但是咱们现在是学习又不是工作，尽量读一些奇怪的代码有助于提高读代码能力（可着劲找借口··）

好了下面放上完整代码：

 #include<iostream>

 using namespace std;

 int total = ;
 int N = ;
 int ans[] = {  }; //结果还是要用数组存滴
 void showOneSolution()//用来显示一个解
 {
     total++;
     for (int i = ; i<=N; ++i)
     {
         cout << ans[i] << " ";
     }
         cout << endl;
 }
 void Dfs(int i,int left,int col,int right)//分别是 层数  反斜杠mark  一列mark  斜杠mark
 {
     if (i > N)              //判断是否已经枚举完了N行
     {
         showOneSolution();  //枚举完了就输出（此刻我们处于N+1行）
         return;             //返回到第N行
     }
     for (int j = N-; j >=; --j) //为啥J倒过来数呢？方便下面if中的偏移判断
     {
         if (!(((left|col|right)>>j)&))//(自己解读，有助于提升能力 )
         {
             ans[i] = N-j;
             Dfs(i + ,(left|(<<j))<<,(col|(<<j)),(right|(<<j))>>);  //更新“占用信息”的工作就放在参数传递这里了
                                               //这样子的好处就是，回溯的时候不用做什么恢复处理，
                                               //因为这一层的东西基本没变动
         }
     }
 }

 int main()
 {
     cin >> N;
     Dfs(,,,);
     cout << total;
     system("pause");
     return ;
 }

---

总结：

　　巧妙运用位运算可以达到锦上添花的效果（装逼），不过大多数人看到位运算&|^<<>>啥的就打哈欠。

　　但是恰巧就有那么一些问题，能够完美契合二进制和位运算的特殊性质（不是指这个==)，当你遇到的时候，你就会惊异于0101010···的奇妙。