最短路径(Dijskra算法）

声明：图片及内容基于：https://www.bilibili.com/video/BV16C4y1H7Zc?from=articleDetail

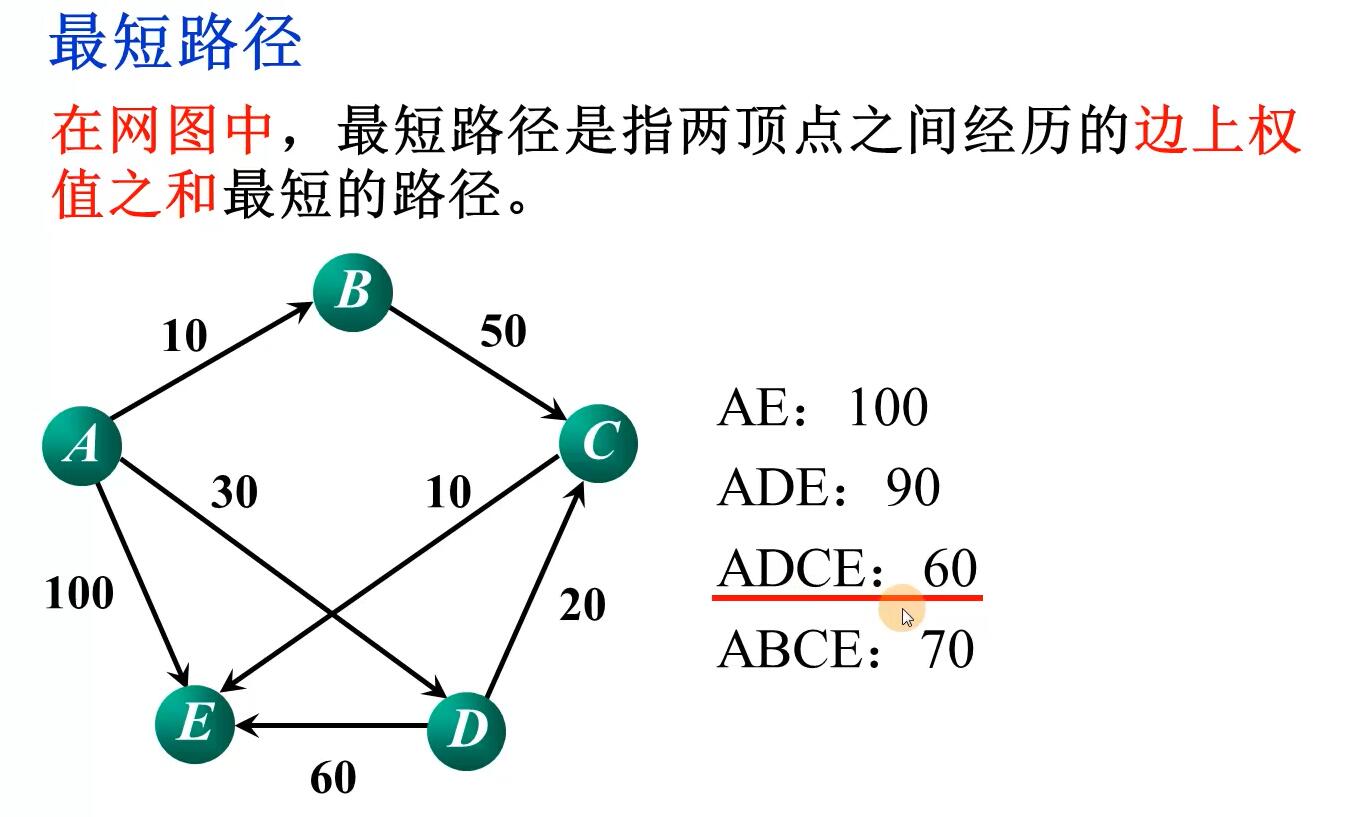
最短路径

Dijkstra算法

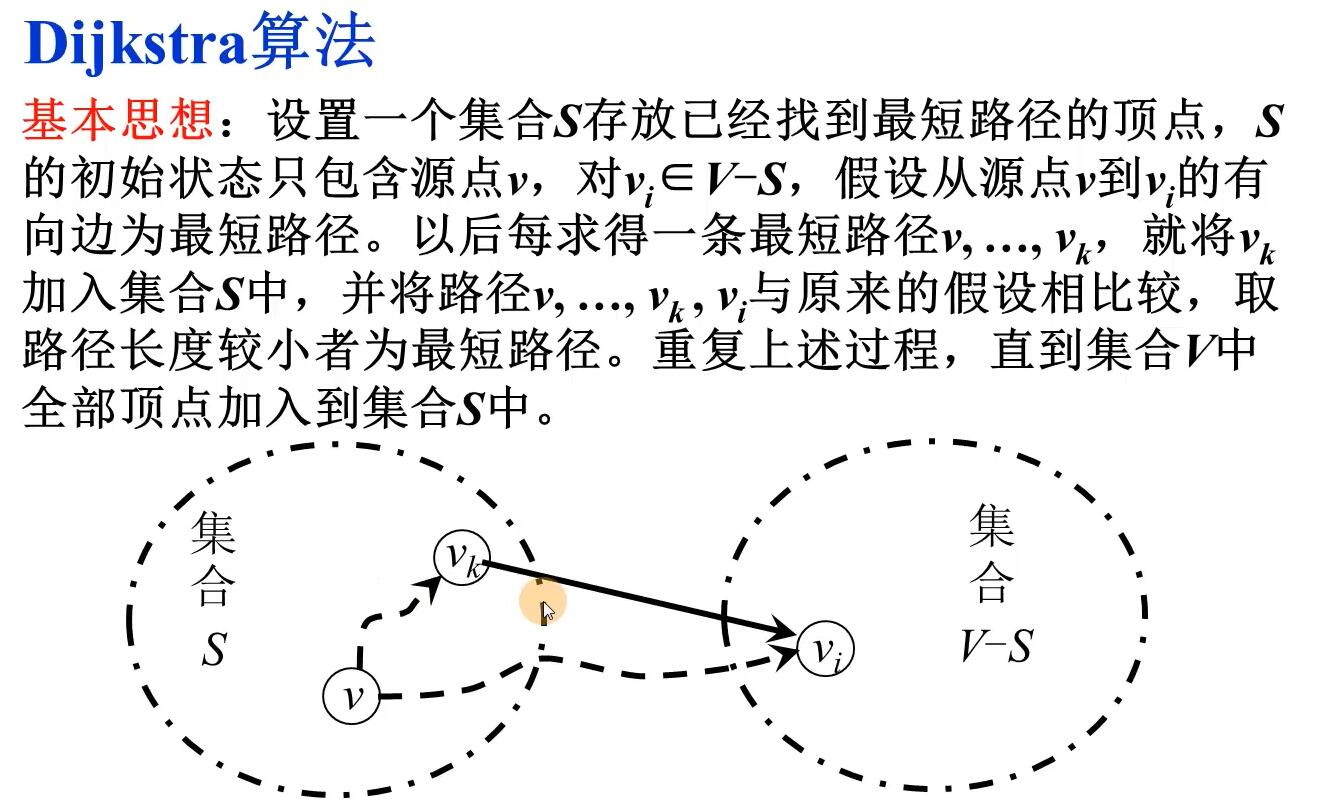
原理

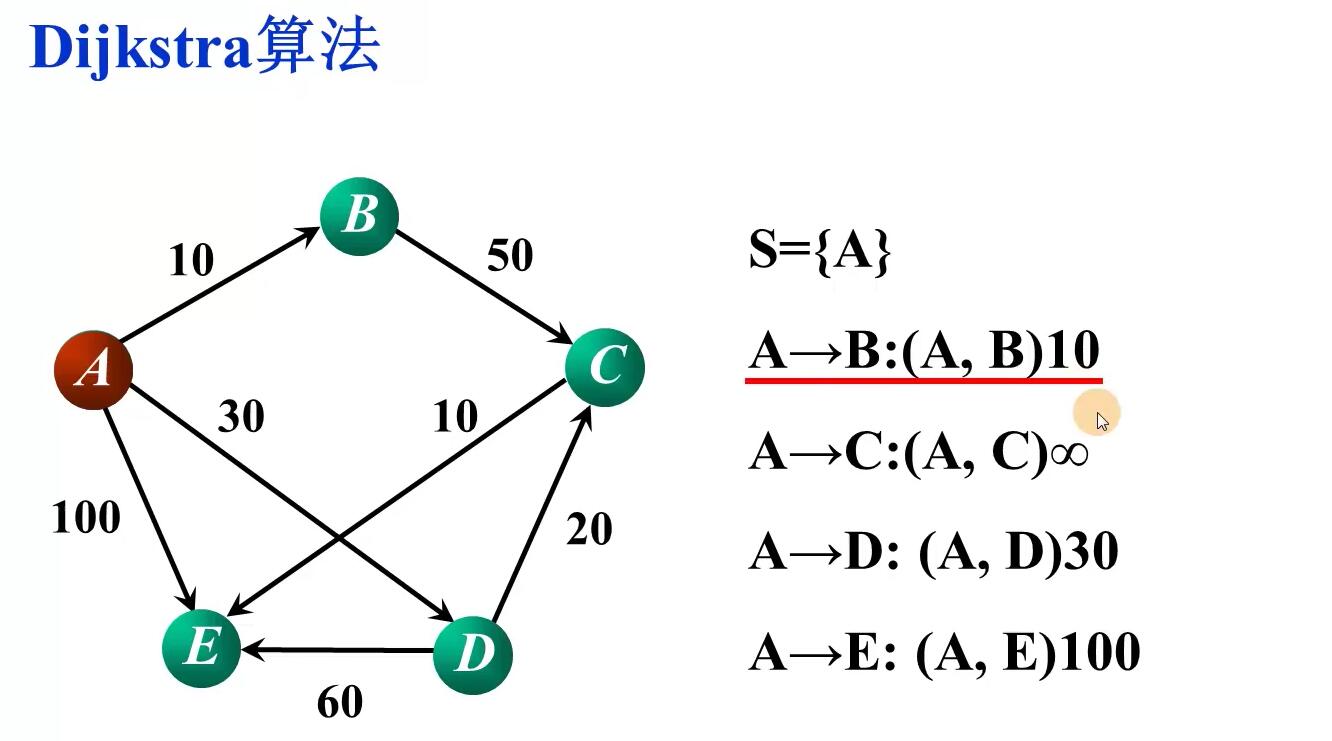
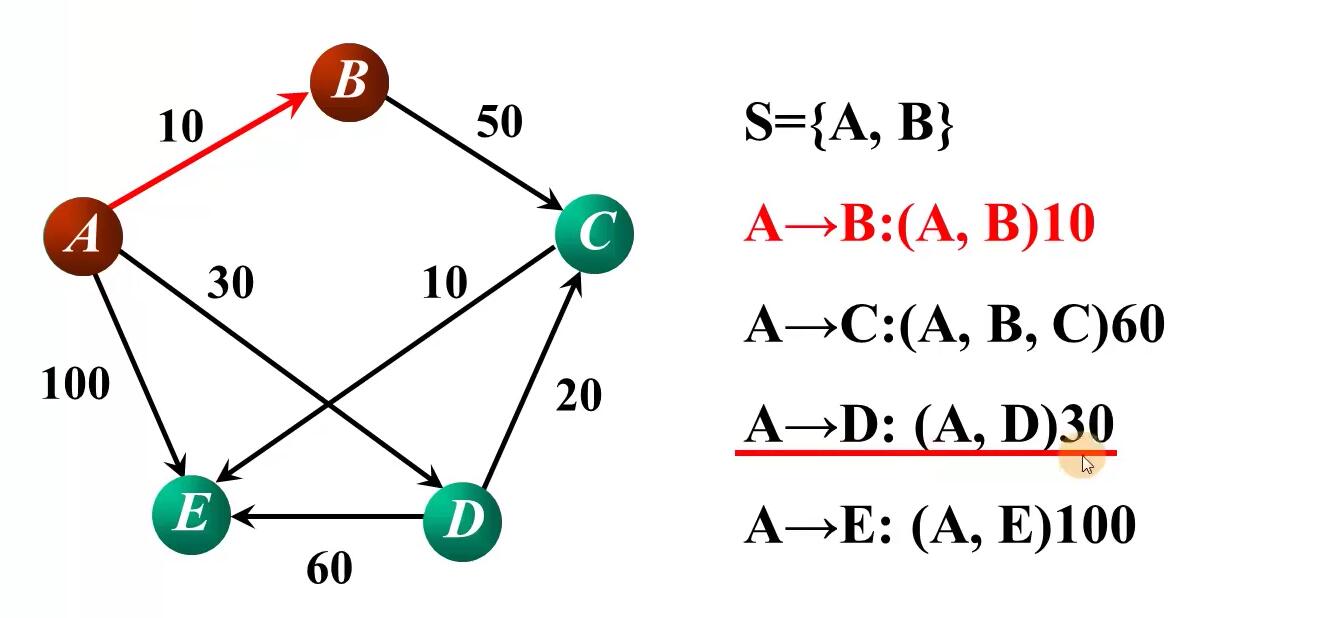
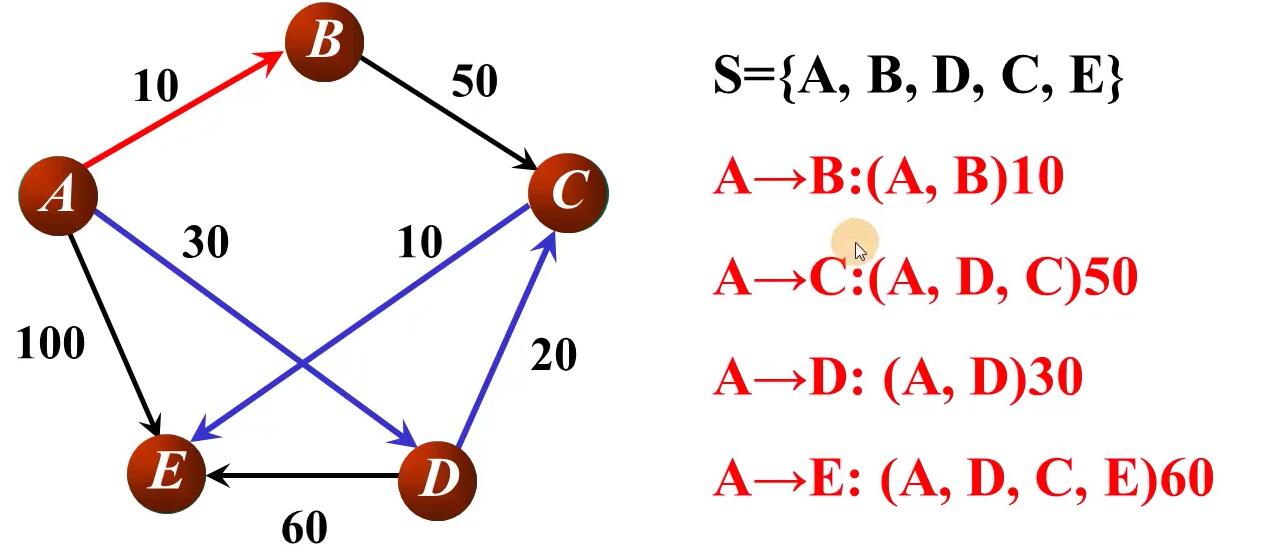
数据结构

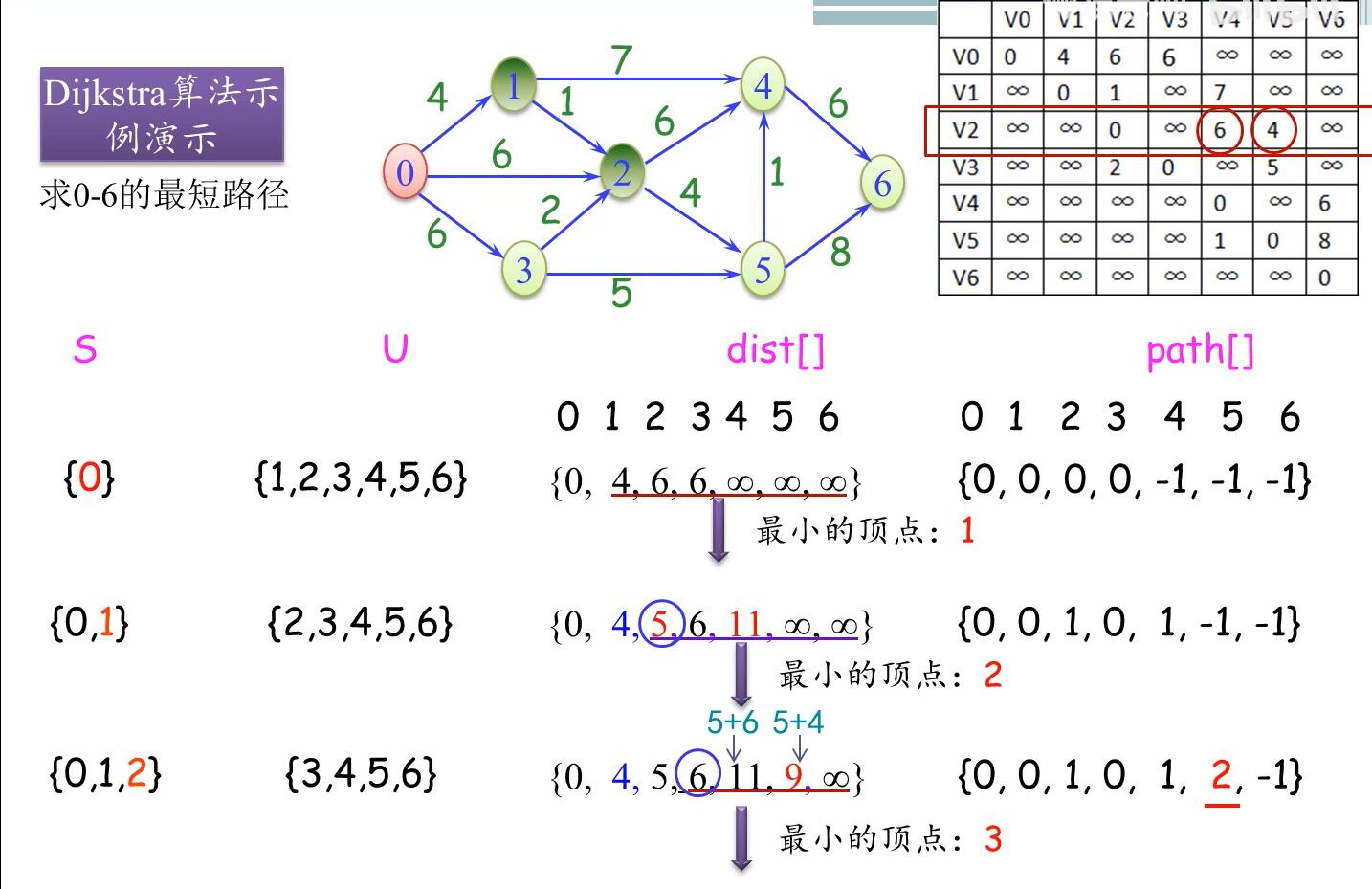
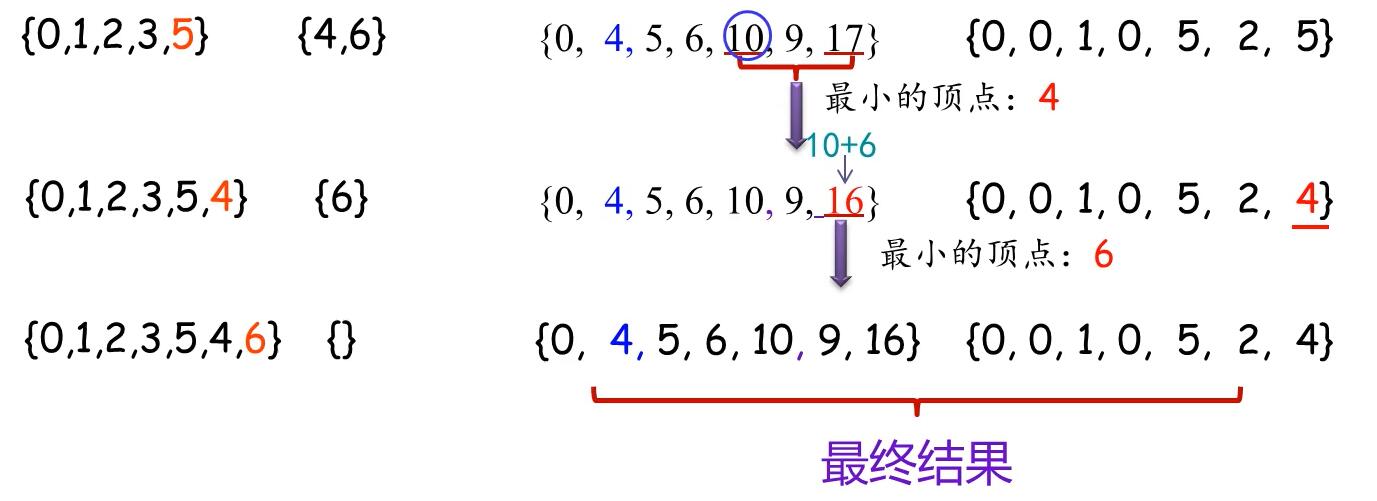
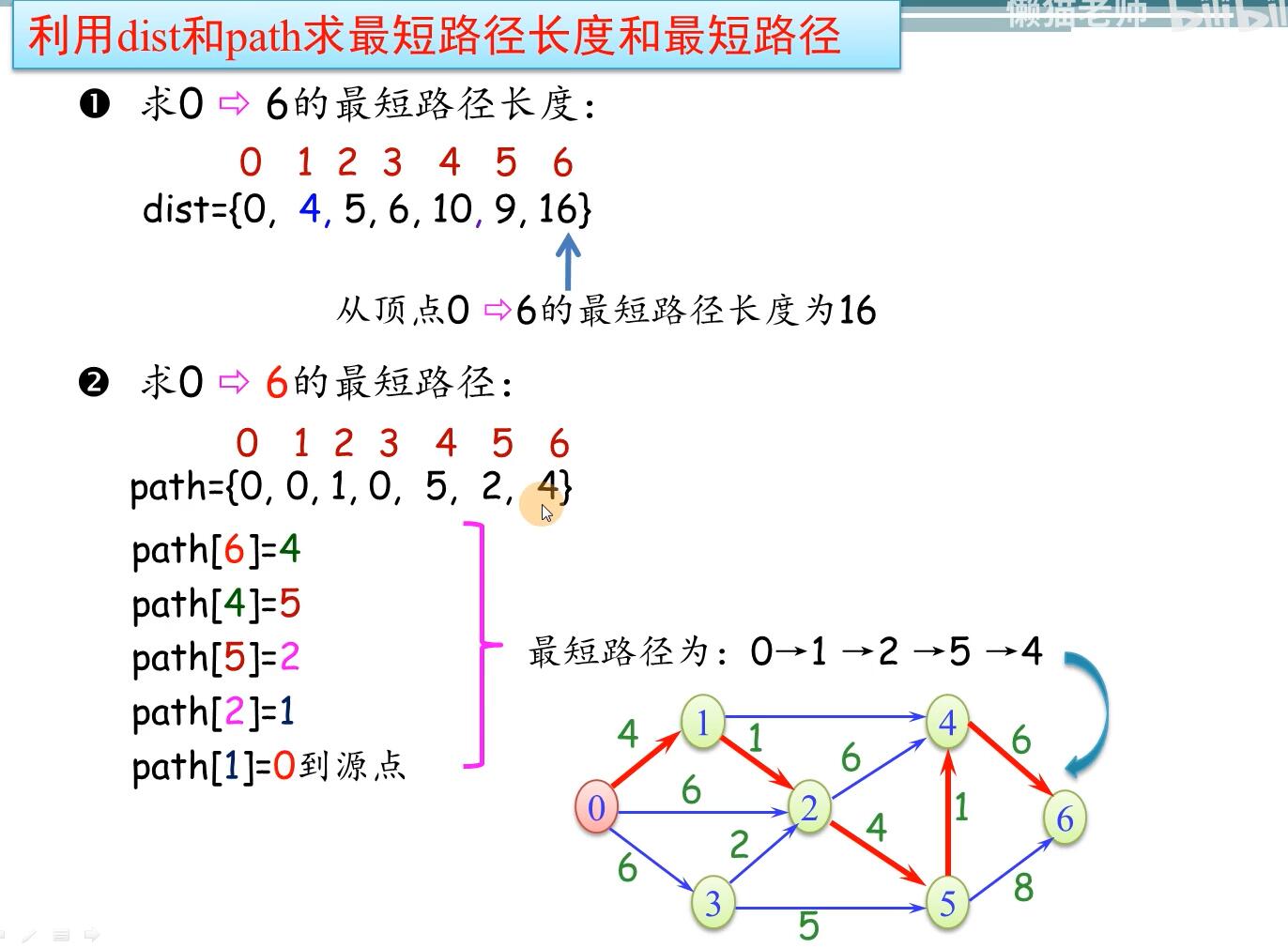
核心代码

findMinDist()

int MGraph::findMinDist(){
    int length=INFINIT;
    for(int i=0;i<vertexNum;i++){
        if(s[i]==0){
            if(length>dist[i]&&dist[i]!=0&&dist[i]!=INFINIT){
                length=i;   //注意记录的是下标，我原来写成length=dist[i]了，太惨了
            }
        }
    }
    return length;
}

displayPath()

void MGraph::displayPath(){            //打印最短路径
    for(int i=0;i<vertexNum;i++){
        if(i==startV) cout<<i<<endl;   //起点直接打印
        if(i!=startV){                 //其他结点
            int tmp=i;
            stack<int> s;              //逆序输出使用栈
            while(tmp!=startV){
                s.push(path[tmp]);
                tmp=path[tmp];
            }
            while(!s.empty()){
                cout<<s.top()<<"->";
                s.pop();
            }
            cout<<i;
            cout<<endl;
        }
    }
}

Dijkstra(int startV)

void MGraph::Dijkstra(int startV){
    this->startV=startV;            //别忘了，startV也是MGraph的数据成员
    for(int i=0;i<vertexNum;i++){
        dist[i]=arc[startV][i];     //dist数组初始化 

        if(dist[i]!=INFINIT)        //path数组初始化
            path[i]=startV;
        else
            path[i]=-1;
    }
    for(int i=0;i<vertexNum;i++)    //s数组初始化
        s[i]=0;

    s[startV]=1;                    //startV放入集合
    int num=1;                      //集合数据个数1
    while(num<vertexNum){
        int min=findMinDist();      //min是当前dist数组中最短路径的下标，前提是s[i]=0，即查找的
                                    //是集合的补集元素
        s[min]=1;                   //min放入集合
        for(int i=0;i<vertexNum;i++){      //更新dist和path数组
            if(s[i]==0&&(dist[i]>dist[min]+arc[min][i])){
                dist[i]=dist[min]+arc[min][i];
                path[i]=min;
            }
        }
        num++;
    }
    displayPath();        //显示全部最短路径
}

完整代码

#include<iostream>
#define MAX 50
#define INFINIT 65535
#include <stack>
using namespace std;
class MGraph{
    private:
        int vertexNum,arcNum;    //顶点数，边数
        int arc[MAX][MAX];       //邻接矩阵
        int vertex[MAX];  //顶点信息
        int dist[MAX];      //记录单源到每个点的最短路径的长度
        int path[MAX];      //记录当前从某点到某点的最短路径，存放的是某点起点的顶点信息
        int s[MAX];         //记录已经确定的最短路径的结点集合
        int startV;
    public:
        MGraph(int v[],int n,int e);
        void display();
        void Dijkstra(int startV);
        int findMinDist();
        void displayPath();
        void displayDistPathS();
};
void MGraph::displayDistPathS(){
    cout<<"dist:"<<endl;
    for(int i=0;i<vertexNum;i++){
        cout<<dist[i]<<" ";
    }
    cout<<endl;
    cout<<"path:"<<endl;
    for(int i=0;i<vertexNum;i++){
        cout<<path[i]<<" ";
    }
    cout<<endl;
    cout<<"S:"<<endl;
    for(int i=0;i<vertexNum;i++){
        cout<<s[i]<<" ";
    }
    cout<<endl;
}
MGraph::MGraph(int v[],int n,int e){   //n是顶点数，e是边数
    vertexNum=n;
    arcNum=e;
    for(int i=0;i<vertexNum;i++){
        vertex[i]=v[i];
    }
    for(int i=0;i<arcNum;i++){        //初始化邻接矩阵
        for(int j=0;j<arcNum;j++){
            if(i==j) arc[i][j]=0;
            else arc[i][j]=INFINIT;
        }
    }
    int vi,vj,w;
    for(int i=0;i<arcNum;i++){
        cout<<"请输入有向边的两个顶点和这条边的权值"<<endl;
        cin>>vi>>vj>>w;   //输入边依附的两个顶点的编号 和权值
        arc[vi][vj]=w; //有边标志
    }
}
void MGraph::display(){
    cout<<"邻接矩阵："<<endl;
    for(int i=0;i<vertexNum;i++){
        for(int j=0;j<vertexNum;j++){
            if(arc[i][j]==INFINIT)
                cout<<"∞"<<"\t";
            else cout<<arc[i][j]<<"\t";
        }
        cout<<endl;
    }
    cout<<endl;
    cout<<"结点信息："<<endl;
    for(int i=0;i<vertexNum;i++){
        cout<<vertex[i]<<" ";
    }
    cout<<endl;
}
int MGraph::findMinDist(){
    int length=INFINIT;
    for(int i=0;i<vertexNum;i++){
        if(s[i]==0){
            if(length>dist[i]&&dist[i]!=0&&dist[i]!=INFINIT){
                length=i;   //注意记录的是下标，我原来写成length=dist[i]了，太惨了
            }
        }
    }
    return length;
}
void MGraph::displayPath(){            //打印最短路径
    for(int i=0;i<vertexNum;i++){
        if(i==startV) cout<<i<<endl;   //起点直接打印
        if(i!=startV){                 //其他结点
            int tmp=i;
            stack<int> s;              //逆序输出使用栈
            while(tmp!=startV){
                s.push(path[tmp]);
                tmp=path[tmp];
            }
            while(!s.empty()){
                cout<<s.top()<<"->";
                s.pop();
            }
            cout<<i;
            cout<<endl;
        }
    }
}
void MGraph::Dijkstra(int startV){
    this->startV=startV;            //别忘了，startV也是MGraph的数据成员
    for(int i=0;i<vertexNum;i++){
        dist[i]=arc[startV][i];     //dist数组初始化 

        if(dist[i]!=INFINIT)        //path数组初始化
            path[i]=startV;
        else
            path[i]=-1;
    }
    for(int i=0;i<vertexNum;i++)    //s数组初始化
        s[i]=0;

    s[startV]=1;                    //startV放入集合
    int num=1;                      //集合数据个数1
    while(num<vertexNum){
        int min=findMinDist();      //min是当前dist数组中最短路径的下标，前提是s[i]=0，即查找的
                                    //是集合的补集元素
        s[min]=1;                   //min放入集合
        for(int i=0;i<vertexNum;i++){      //更新dist和path数组
            if(s[i]==0&&(dist[i]>dist[min]+arc[min][i])){
                dist[i]=dist[min]+arc[min][i];
                path[i]=min;
            }
        }
        num++;
    }
    displayPath();        //显示全部最短路径
}

int main(){
    int n,e;
    int v[MAX];
    cout<<"请输入顶点数和边数"<<endl;
    cin>>n>>e;
    cout<<"请输入顶点信息"<<endl;
    for(int i=0;i<n;i++){
        cin>>v[i];
    }
    cout<<"请输入起点："<<endl;
    int t;
    cin>>t;
    MGraph mgraph(v,n,e);
    mgraph.display();
    mgraph.Dijkstra(t);
    mgraph.displayDistPathS();
    return 0;
}

输入：

7 12
0 1 2 3 4 5 6
0
0 1 4
0 2 6
0 3 6
1 2 1
1 4 7
2 4 6
2 5 4
3 2 2
3 5 5
4 6 6
5 4 1
5 6 8

输出：

邻接矩阵：
0 4  6  6 ∞  ∞ ∞
∞ 0 1  ∞ 7  ∞ ∞
∞ ∞ 0 ∞ 6  4 ∞
∞ ∞ 2 0 ∞  5 ∞
∞ ∞ ∞ ∞ 0  ∞ 6
∞ ∞ ∞ ∞ 1  0 8
∞ ∞ ∞ ∞ ∞ ∞ 0

结点信息：
0 1 2 3 4 5 6
0
0->1
0->1->2
0->3
0->1->4
0->1->2->5
0->1->4->6
dist:
0 4 5 6 11 9 17
path:
0 0 1 0 1 2 4
S:
1 1 1 1 1 1 1