2021-2-22：请你说下 CAP 理论并举例

CAP

CAP 理论是分布式系统中的一个老生常谈的理论了，最早由 Eric Brewer 在一个讲座中提出。在这个讲座中，在传统 ACID 理论以及当时比较流行但是比较抽象的的设计指导理论 BASE 理论（当时的 BASE 理论还很抽象，直到好几年后才出现一份比较权威的被广泛接受的 BASE 理论完整解释和设计）的类比中，提出

• C(Consistency，一致性)：在一个分布式的系统中，同一个数据的所有备份，在同一时刻是否有相同的值。也就是，对于同一个数据的读写，是否立刻对于所有副本都能看到一致的结果。一种比较常见的强一致性实现就是，在看到一致的结果之前，写请求不返回，读请求阻塞或者超时。
• A(Availability，可用性)：在集群中一些节点故障时，集群还可以响应读写请求。
• P(Partition-tolerance，分区容忍性)：分布式系统具有多个节点，如果节点间网络中断，就会造成分区。

并且提出了，CAP 并不能全部满足，而是一般选两个满足

之后，Seth Gilbert 以及 Nancy Lynch 在一篇 Notes中，证明了 CAP 并不能同时都满足。并且，将 CAP 定义的更加清晰：

• C: 需要满足原子一致性，也就是任何读写都是具有原子性的，也就是对于同一个数据的写之后的读取，一定能读取到写的值，也就是最新的值
• A：对于所有成功的请求，都需要在有限的时间内返回，也就是成功请求是有效的，可终止的。
• P：可能节点间传输丢失一些消息。

CA 系统

也就是不允许分区的系统，也其实就不是分布式系统，而是单机系统。例如单机数据库，或者是共享存储数据库，比如 Aurora DB 类似的思路设计的数据库，共享同一份存储，上面建立不同的 MySQL 进程，一个 MySQL 读写，其他的只读，由于使用的同一块存储，并且只有一个 MySQL 进程写入，满足 ACID 的事务特性，能保证强一致性，以及可用性。

CP 系统

也就是不要求高可用性，但是要求强一致性的系统，哪怕当前业务不可用，也不能出现数据不一致的情况。并且，如果节点间传输消息丢失导致没有同步成功，或者重试，或者返回更新失败，回滚更新请求。

CP 的一种实际应用就是分布式锁，一般的，如果没有获取到锁，或者获取锁失败，我们都会选择阻塞等待，或者直接失败，而不会冒着可能会有并发危险而去执行业务。并且，分布式锁必须保持所有节点看到的锁状态一致，不能有差异，否则认为获取锁失败。

同时，大部分分布式数据库都是 CP 系统，但是他们的一致性协议方案是不同的，常见的例如 Paxos，2PC，3PC，RAFT等等。

AP 系统

也就是要求高可用性，但是不用强一致性的系统。在这种情况下，一旦分区发生，节点间的数据可能不一致，每个节点用自己的本地数据继续提供服务。这样情况下，可能会出现数据不一致，系统一般会实现最终一致性。也就是在分区结束后，通过一些机制将数据同步。

基本上具有多层缓存的系统，都是 AP 的系统设计。例如 DNS，客户端缓存，浏览器缓存以及进程内缓存等等。

一个 CP 与 AP 系统的对比

一个比较经典的例子就是 Zookeeper 作为注册中心和 Eureka 作为注册中心。

假设注册中心有两个接口，一个是注册实例，一个是读取实例。

如果以 Zookeeper 为注册中心，对于注册实例请求也就是更新请求，采用的是过半写以及 2 PC 的同步机制。

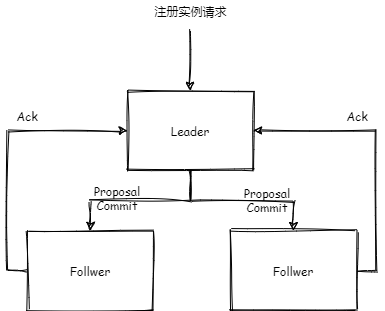
只有过半 2PC 更新成功，这个注册请求才成功，这样读取每个节点都会读取到这个更新请求，否则会回滚已经更新的节点。并且每个节点数据是一致的。如果过半的节点不可用，那么整个集群都不能处理注册实例请求以及读取实例的请求。这样保证的强一致性，但是可用性是打了折扣的。

如果以 Eureka 为注册中心，注册请求发到一个 Eureka 实例上之后，这个 Eureka 会转发到集群内其他 Eureka 节点。

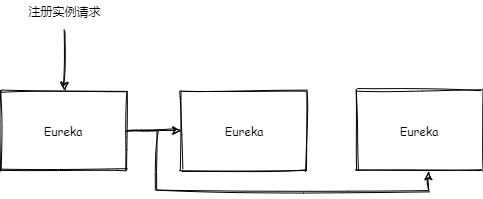
即使某些节点失败，也不会将已经更新的回滚。并且无论集群内哪些 Eureka 挂了，也不会影响其他正常的 Eureka 继续服务工作，虽然可能读取到比较老的数据，以及有一些数据不一致。

目前的 CAP 理论

随着技术的不断发展以及理论的不断完善，我们发现，分区并不是会经常出现的情况，大部分情况下，如果我们忽略 P ，其实就是可以实现 CA 共存的情况。如果分区是可以感知的，纳闷我们可以提前制定响应策略，例如进入服务降级限制某些操作，通过恢复补偿逻辑修正数据不一致。

在 CAP 基础上演变的 PACELC 理论，就是针对这种情况的更为实际的指导意见。在出现分区的情况下，取前半部分，其实还是 CAP 理论。如果不出现分区的情况，也就是大部分的情况下，我们考虑 L（Latency，延迟） 与 C（Consistency 一致性）的权衡。

微信搜索“我的编程喵”关注公众号，每日一刷，轻松提升技术，斩获各种offer：