Java数据结构（十）—— 树
树
树的概念和常用术语
常用术语
节点
根节点
父节点
子节点
叶子节点：没有子节点的节点
节点的权：节点的值
路径：节点A到节点B的路径
层
子树
树的高度：最大层数
森林：多颗子树构成森林
二叉树概念
每个节点最多只有两个子节点的树，叫二叉树
若该二叉树是满二叉树，节点数是2^n - 1，n为层数
完全二叉树：每一层节点都是连续的，即有子节点的父节点都有两个子节点
建立二叉树
思路分析
建立节点类
包含信息，左孩子指针，右孩子指针
二叉树的前中后序遍历算法
前序遍历
前序遍历
先输出父节点，再遍历左子树和右子树
中，左，右
思路分析
先输出当前节点，初始是root节点
如果左子节点不为空，则递归继续前序遍历
如果右子节点不为空，则递归继续前序遍历
中序遍历
中序遍历
先遍历左子树，在输出父节点，再遍历右子树
左，中，右
思路分析
如果左子节点不为空，则递归继续中序遍历
输出当前节点
如果右子节点不为空，则递归继续中序遍历
后序遍历
后序遍历
先遍历左子树，再遍历右子树，最后输出父节点
左，右，中
思路分析
如果左子节点不为空，则递归继续中序遍历
如果右子节点不为空，则递归继续中序遍历
输出当前节点
代码实现
package com.why.tree;
import java.sql.SQLOutput;
/**
* @Description TODO 前中后序遍历
* @Author why
* @Date 2020/11/4 16:49
* Version 1.0
**/
public class BinaryTreeDemo {
public static void main(String[] args) {
//创建二叉树
BinaryTree binaryTree = new BinaryTree();
//创建需要的节点
BNode root = new BNode(1,"why");
BNode node1 = new BNode(1,"cjl");
BNode node2 = new BNode(1,"wl");
BNode node3 = new BNode(1,"lrx");
//手动创建二叉树，后边以递归方式建立二叉树
root.setLeftChild(node1);
root.setRightChild(node2);
node2.setRightChild(node3);
//设置根节点
binaryTree.setRoot(root);
System.out.println("前序遍历：");
binaryTree.preOrder();
System.out.println();
System.out.println("中序遍历：");
binaryTree.midOrder();
System.out.println();
System.out.println("后序遍历：");
binaryTree.postOrder();
}
}
/**
* 定义二叉树
*/
class BinaryTree{
private BNode root;
public BNode getRoot() {
return root;
}
public void setRoot(BNode root) {
this.root = root;
}
/**
* 前序遍历
*/
public void preOrder(){
if (this.root != null){
this.root.preOrder();
}else {
System.out.println("二叉树为空");
}
}
/**
* 中序遍历
*/
public void midOrder(){
if (this.root != null){
this.root.midOrder();
}else {
System.out.println("二叉树为空");
}
}
/**
* 后序遍历
*/
public void postOrder(){
if (this.root != null){
this.root.postOrder();
}else {
System.out.println("二叉树为空");
}
}
}
/**
* 创建节点类
*/
class BNode{
private int id;
private String name;
private BNode leftChild;//左孩子节点
private BNode rightChild;//右孩子节点
public BNode(int id, String name) {
this.id = id;
this.name = name;
}
public int getId() {
return id;
}
public void setId(int id) {
this.id = id;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public BNode getLeftChild() {
return leftChild;
}
public void setLeftChild(BNode leftChild) {
this.leftChild = leftChild;
}
public BNode getRightChild() {
return rightChild;
}
public void setRightChild(BNode rightChild) {
this.rightChild = rightChild;
}
@Override
public String toString() {
return "BNode{" +
"id=" + id +
", name='" + name+
'}';
}
/**
* 前序遍历
*/
public void preOrder(){
//先输出当前(父节点）节点
System.out.println(this);
//递归左子树
if (this.leftChild != null){
this.leftChild.preOrder();
}
//递归右子树
if (this.rightChild != null){
this.rightChild.preOrder();
}
}
/**
* 中序遍历
*/
public void midOrder(){
//先中序遍历左子树
if (this.leftChild != null){
this.leftChild.midOrder();
}
//输出当前节点
System.out.println(this);
//中序遍历右子树
if (this.rightChild != null){
this.rightChild.midOrder();
}
}
/**
* 后序遍历
*/
public void postOrder(){
//后序遍历左子树
if (this.leftChild != null){
this.leftChild.preOrder();
}
//后序遍历右子树
if (this.rightChild != null){
this.rightChild.postOrder();
}
//输出当前节点
System.out.println(this);
}
}
二叉树的前中后序查找算法
前序查找
思路分析
和当前节点比较，若相等返回当前节点
若不相等
左子树不为空，左递归前序查找，找到节点返回
右子树不为空，右递归前序查找，找到节点返回，找不到显示没有搜索结果
代码实现
节点类
/**
* 前序查找
* @param no
* @return
*/
public BNode preSearch(int no){
if (this.getId() == no){//与当前节点比较，相等返回
return this;
}
//遍历左子树查找
BNode bNode = null;
if (this.leftChild != null){
bNode = this.leftChild.preSearch(no);
}
if (bNode != null){//左子树找到
return bNode;
}
//遍历右子树
if (this.rightChild != null){
bNode = this.rightChild.preSearch(no);
}
return bNode;
}
二叉树类
/**
* 前序查找
* @param no
*/
public void preSearch(int no){
if (this.root != null){
BNode bNode = this.root.preSearch(no);
if (bNode != null){
System.out.println(bNode);
}else {
System.out.println("未找到");
}
}else {
System.out.println("二叉树为空");
}
}
中序查找
思路分析
左子树不为空，左递归中序查找，找到节点返回
若未找到
和当前节点比较，若相等返回当前节点
右子树不为空，右递归中序查找，找到节点返回，找不到显示没有搜索结果
代码实现
节点类
/**
* 中序查找
* @param no
* @return
*/
public BNode midSearch(int no){
BNode bNode = null;
//遍历左子树
if (this.leftChild != null){
bNode = this.leftChild.midSearch(no);
}
if (bNode != null){
return bNode;
}
//与当前节点比较
if (this.getId() == no){
return this;
}
//遍历右子树
if (this.rightChild != null){
bNode = this.rightChild.midSearch(no);
}
return bNode;
}
二叉树类
/**
* 中序查找
* @param no
*/
public void midSearch(int no){
if (this.root != null){
BNode bNode = this.root.midSearch(no);
if (bNode != null){
System.out.println(bNode);
}else {
System.out.println("未找到");
}
}else {
System.out.println("二叉树为空");
}
}
后序查找
思路分析
左子树不为空，左递归后序查找，找到节点返回
若未找到
右子树不为空，右递归后序查找，找到节点返回
和当前节点比较，若相等返回当前节点，找不到显示没有搜索结果
代码实现
节点类
/**
* 后序查找
* @param no
* @return
*/
public BNode postSearch(int no){
BNode bNode = null;
//遍历左子树
if (this.leftChild != null){
bNode = this.leftChild.postSearch(no);
}
if (bNode != null){
return bNode;
}
//遍历右子树
if(this.rightChild != null){
bNode = this.rightChild.postSearch(no);
}
if (bNode != null){
return bNode;
}
//与当前节点比较
if (this.getId() == no){
bNode = this;
}
return bNode;
}
二叉树类
/**
* 后序查找
* @param no
*/
public void postSearch(int no){
if (this.root != null){
BNode bNode = this.root.postSearch(no);
if (bNode != null){
System.out.println(bNode);
}else {
System.out.println("未找到");
}
}else {
System.out.println("二叉树为空");
}
}
删除二叉树指定的节点
要求
若删除的是叶子节点，则删除该节点
如果删除的节点是非叶子节点，则删除该子树
思路
因为二叉树是单向的，所以判断 当前节点的子节点是否是待删除的节点
不能判断当前节点是不是需要删除的节点
如果当前节点的左孩子节点不为空，并且左孩子节点是待删除的节点将this.left置空，返回
如果当前节点的左孩子节点不为空，并且左孩子节点是待删除的节点将this.left置空，返回
如果上述步骤，没有删除节点，那么就需要向左/右子树递归删除
如果只有一个root节点，则等价于将二叉树指控
代码实现
BNode.java
/**
* 删除指定的节点
* @param no
*/
public void delete(int no){
if(this.getLeftChild() != null && this.getLeftChild().getId() == no){
this.setLeftChild(null);
return;
}
if (this.getRightChild() != null && this.getRightChild().getId() == no){
this.setRightChild(null);
return;
}
//向左子树递归
if (this.getRightChild() != null){
this.getLeftChild().delete(no);
}
//向右子树递归
if (this.getRightChild() != null){
this.getRightChild().delete(no);
}
}
BinaryTree.java
/**
* 根据id删除节点/子树
* @param no
*/
public void delete(int no){
if (this.root != null){
if(this.root.getId() == no){
this.root = null;
}else {
this.root.delete(no);
}
}else {
System.out.println("二叉树为空");
}
}
顺序存储二叉树
存储结构
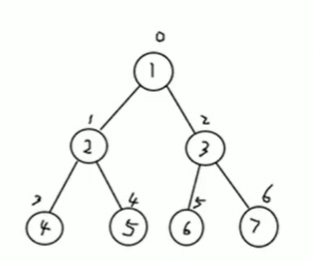
要求
上图二叉树的节点，要求以数组的方式来存放[1,2,3,4,5,6,]
但是仍然能够以树的形式来遍历
顺序存储二叉树的特点
顺序二叉树通常只考虑完全二叉树
第n个元素的左孩子节点是2*n + 1
第n个元素的右子节点是2*n + 2
第n个元素的父节点为（n-1)/2
代码实现
package com.why.tree;
/**
* @Description TODO
* @Author why
* @Date 2020/11/12 15:14
* Version 1.0
**/
public class ArrBinaryTreeDemo {
public static void main(String[] args) {
int[] arr = {1,2,3,4,5,6,7};
ArrBinaryTree abt = new ArrBinaryTree(arr);
// abt.preOrder();
// abt.midOrder();
abt.postOrder();
}
}
class ArrBinaryTree{
private int[] arr;
public ArrBinaryTree(int[] arr) {
this.arr = arr;
}
/**
* 顺序存储二叉树的前序遍历
* @param index 数组的下标
*/
public void preOrder(int index){
//如果数组为空，或者arr.length == 0
if (arr == null || arr.length == 0){
System.out.println("数组为空不能按照二叉树进行前序遍历");
}
//输出当前元素
System.out.println(arr[index]);
//向左递归遍历
if ((2 * index +1) < arr.length){
preOrder(2 * index +1);
}
//向右递归
if ((2 * index +2) < arr.length){
preOrder(2 * index +2);
}
}
/**
* 重载方法
*/
public void preOrder(){
this.preOrder(0);
}
/**
* 中序遍历
* @param index
*/
public void midOrder(int index){
if (arr == null || arr.length == 0){
System.out.println("数组为空");
}
//左递归
if ((2 * index + 1) < arr.length){
midOrder(2 * index + 1);
}
//输出当前元素
System.out.println(arr[index]);
if ((2 * index + 2) < arr.length){
midOrder(2 * index + 2);
}
}
public void midOrder(){
midOrder(0);
}
/**
* 后序遍历
* @param index
*/
public void postOrder(int index){
if (arr == null || arr.length == 0){
System.out.println("数组为空");
}
//左递归
if ((2 * index + 1) < arr.length){
postOrder(2 * index + 1);
}
//右递归
if ((2 * index + 2) < arr.length){
postOrder(2 * index + 2);
}
//输出当前元素
System.out.println(arr[index]);
}
public void postOrder(){
postOrder(0);
}
}
作用：堆排序用到二叉树的顺序存储
线索化二叉树
基本介绍
n个节点的二叉链表中含有n+1个空指针域。利用二叉链表中的空指针域，存放指向节点在某种遍历次序下的前驱和后继节点的指针（附加的指针叫线索）
加上了线索的二叉链表叫做线索链表，相应的二叉树称为线索二叉树（threaded BinaryTree）根据线索性质不同，线索二叉树可分为前序线索二叉树，中序线索二叉树，后序线索二叉树三种
一个节点的前一节点是前驱节点
一个节点的后一节点是后继结点
说明
当线索化二叉树后，Node节点的属性left和right，有如下情况：
left指向的是左子树，也可能指向前驱节点
right指向右子树也可能指向后继结点
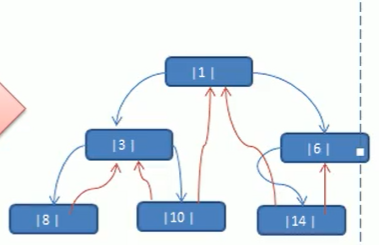
代码实现
package com.why.tree;
import javax.swing.*;
/**
* @Description TODO
* @Author why
* @Date 2020/11/24 15:08
* Version 1.0
**/
public class ThreadBinaryTreeDemo {
public static void main(String[] args) {
//测试中序线索二叉树
int[] arr = {8,3,10,1,14,6};
Node root = new Node(1);
Node node1 = new Node(3);
Node node2 = new Node(6);
Node node3= new Node(8);
Node node4 = new Node(10);
Node node5 = new Node(14);
//手动创建二叉树
ThreadBinaryTree tbt = new ThreadBinaryTree(root);
root.setLeft(node1);
root.setRight(node2);
node1.setLeft(node3);
node1.setRight(node4);
node2.setLeft(node5);
tbt.midOrder();
tbt.threadedNodes();
//测试中序线索化是否正确,验证10号节点前驱后继节点是否正确
System.out.println("前驱："+node4.getLeft());
System.out.println("后继：" + node4.getRight());
}
}
class ThreadBinaryTree{
//定义根节点
private Node root = new Node();
//为实现线索化，创建一个指向当前节点的前驱节点的指针
//递归进行线索化时，pre保留前一个节点
private Node pre = null;
public ThreadBinaryTree(Node root) {
this.root = root;
}
public Node getRoot() {
return root;
}
public void setRoot(Node root) {
this.root = root;
}
/**
* 判空
* @return
*/
boolean isEmpty(){
if (this.root == null){
return true;
}
return false;
}
/**
* 中序线索化
* @param node
*/
public void threadedNodes(Node node){
//如果node == null,不能线索化
if (node == null){
return;
}
//第一步，线索化左子树
threadedNodes(node.getLeft());
//第二步，线索化当前节点
//2.1.处理当前节点的前驱节点
if (node.getLeft() == null){
//当前节点的左指针指向前驱节点
node.setLeft(pre);
//修改当前节点的左指针类型
node.setLeftType(1);
}
//2.2.处理当前节点的后继结点,下一次处理，pre指向上一次node
if (pre != null && pre.getRight() == null){
//让前驱节点的右指针指向当前节点
pre.setRight(node);
//修改前驱节点的右指针类型
pre.setRightType(1);
}
//每处理一个节点后让当前节点是下一个节点的前驱节点
pre = node;
//第三步，线索化右子树
threadedNodes(node.getRight());
}
//重载
public void threadedNodes(){
threadedNodes(root);
}
/**
* 中序遍历
*/
public void midOrder(){
if (this.root != null){
this.root.midOrder();
}else {
System.out.println("二叉树为空");
}
}
}
//线索化二叉树节点
class Node{
private int no;//数值
private Node left;//左孩子节点 || 前驱节点
private Node right;//右孩子节点 || 后继结点
/**
* 说明：
* leftType == 0 表示指向左子树
* leftType == 1 表示指向前驱节点
*/
private int leftType;
/**
* 说明：
* rightType == 0 表示指向有子树
* rightType == 1 表示指向后继结点
*/
private int rightType;
public Node() {
}
public Node(int no) {
this.no = no;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
public int getLeftType() {
return leftType;
}
public void setLeftType(int leftType) {
this.leftType = leftType;
}
public int getRightType() {
return rightType;
}
public void setRightType(int rightType) {
this.rightType = rightType;
}
@Override
public String toString() {
return "Node{" +
"no=" + no +
'}';
}
public void midOrder(){
//遍历左子树
if (this.getLeft() != null){
this.left.midOrder();
}
//输出当前节点
System.out.println(this);
//遍历右子树
if (this.getRight() != null){
this.right.midOrder();
}
}
}遍历线索化二叉树
分析：由于线索化后各个节点的指向有变化，因此原来的遍历方式不能够再去使用
各个节点可以使用线性的方式遍历，无需使用递归，提高了遍历效率，遍历次序应和线索化方式相同
代码实现：
/**
* 中序遍历线索化二叉树
*/
public void midOrder(){
Node node = root;
while (node != null){
//存储当前便利的节，从root开始
//循环找到leftType == 1的节点
while (node.getLeftType() == 0){
node = node.getLeft();
}
//打印当前节点
System.out.println(node);
//如果当前节点的右指针指向的是后继节点就一直输出
while (node.getRightType() == 1){
//获取到当前节点的后继节点
node = node.getRight();
System.out.println(node);
}
//替换这个遍历的节点
node = node.getRight();
}
}
Java数据结构（十）—— 树的更多相关文章
- Java数据结构之树和二叉树（2）
从这里始将要继续进行Java数据结构的相关讲解,Are you ready?Let's go~~ Java中的数据结构模型可以分为一下几部分: 1.线性结构 2.树形结构 3.图形或者网状结构 接下来 ...
- Java数据结构之树和二叉树
从这里开始将要进行Java数据结构的相关讲解,Are you ready?Let's go~~ Java中的数据结构模型可以分为一下几部分: 1.线性结构 2.树形结构 3.图形或者网状结构 接下来的 ...
- java数据结构之树
树定义和基本术语定义树(Tree)是n(n≥0)个结点的有限集T,并且当n>0时满足下列条件: (1)有且仅有一个特定的称为根(Root)的结点: (2)当n>1时,其余结 ...
- Java数据结构——AVL树
AVL树(平衡二叉树)定义 AVL树本质上是一颗二叉查找树,但是它又具有以下特点:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树,并且拥有自平衡机制.在AV ...
- Java数据结构——字典树TRIE
又称单词查找树,Trie树,是一种树形结构,是一种哈希树的变种. 典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计. 它的优点是:利用字符串的公共 ...
- JAVA数据结构--AVL树的实现
AVL树的定义 在计算机科学中,AVL树是最先发明的自平衡二叉查找树.在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树.查找.插入和删除在平均和最坏情况下的时间复杂度都是.增 ...
- Java数据结构——2-3树
定义2-3树是平衡的3路查找树,其中2(2-node)是指拥有两个分支的节点,3(3-node)是指拥有三个分支的节点.B-树是一种平衡的多路查找树,2-3树属于b-树,其也同样具有B-树的性质,如m ...
- java数据结构-12树相关概念
一.树 1.概念: 包含n(n>=0)个结点的有穷集:树有多个节点(node),用以储存元素.某些节点之间存在一定的关系,用连线表示,连线称为边(edge).边的上端节点称为父节点,下端称为子节 ...
- Java数据结构和算法（十四）——堆
在Java数据结构和算法(五)——队列中我们介绍了优先级队列,优先级队列是一种抽象数据类型(ADT),它提供了删除最大(或最小)关键字值的数据项的方法,插入数据项的方法,优先级队列可以用有序数组来实现 ...
- Java数据结构和算法 - 什么是2-3-4树
Q1: 什么是2-3-4树? A1: 在介绍2-3-4树之前,我们先说明二叉树和多叉树的概念. 二叉树:每个节点有一个数据项,最多有两个子节点. 多叉树:(multiway tree)允许每个节点有更 ...
随机推荐
- TypeScript魔法堂：枚举的超实用手册
前言 也许前端的同学会问JavaScript从诞生至今都没有枚举类型,我们不是都活得挺好的吗?为什么TypeScript需要引入枚举类型呢? 也许被迫写前端的后端同学会问,TypeScript的枚举类 ...
- python基础二：循环
python 中循环的方式有两种: 一,for 循环 单向循环 可以用来遍历字符串,列表,元组,字典等 for value in 被遍历对象: print(value) 遍历字典dict的时候稍有不 ...
- 原生JS结合cookie实现商品评分组件
开发思路如下: 1.利用JS直接操作DOM的方式开发商品评分组件,主要实现功能有:显示评价评分的样式以及将用户操作后对应的数据返回到主页面 2.主页面引入商品评分组件的js文件并根据规定格式的数据,生 ...
- 安装Mysql，开发权限，以及复制数据库
官网下载 https://downloads.mysql.com/archives/community/ 解压后安装,管理员身份打开cmd,转到mysql的bin目录,mysqld --ins ...
- python机器学习实现逻辑斯蒂回归
逻辑斯蒂回归 关注公众号"轻松学编程"了解更多. [关键词]Logistics函数,最大似然估计,梯度下降法 1.Logistics回归的原理 利用Logistics回归进行分类的 ...
- 【API进阶之路】API带来的微创新，打动投资人鼓励我创业
摘要:怎么帮助创作者提高视频的推荐量呢?我发现了:视频的封面图非常重要. 上回说到,老板一拍脑门,交代了一个新项目:小成本开发一款短视频剪辑工具([<[API进阶之路]人少钱少需求多的新项目该怎 ...
- Serilog源码解析——使用方法
在上两篇文章(链接1和链接2)中,我们通过一个简易 demo 了解到了一个简单的日志记录类库所需要的功能,即一条日志有哪些数据,以及如何通过一次记录的方式将同一条日志消息记录到多个日志媒介中.在本文中 ...
- 云计算之路-出海记-小目标：Hello World from .NET 5.0 on AWS
品尝过船上的免费晚餐,眺望着 aws 上搭建博客园海外站的宏伟目标,琢磨着眼前可以实现的小目标,不由自主地在屏幕上敲出了 -- "Hello World!",就从这个最简单朴实的小 ...
- 深入探索Spring Data JPA， 从Repository 到 Specifications 和 Querydsl
数据访问层,所谓的CRUD是后端程序员的必修课程,Spring Data JPA 可以让我们来简化CRUD过程,本文由简入深,从JPA的基本用法,到各种高级用法. Repository Spring ...
- Docker 实战（3）- 搭建 Gitlab 容器并上传本地项目代码
如果你还想从头学起 Docker,可以看看这个系列的文章哦! https://www.cnblogs.com/poloyy/category/1870863.html 搭建 Gitlab 容器 搜索 ...