机器学习作业---K-Means算法

--------------------------K-Means算法使用--------------------------

一：数据导入及可视化

import numpy as np
import matplotlib.pyplot as plt
import scipy.io as sio

data = sio.loadmat("ex7data2.mat")
X = data['X']　　
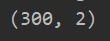
print(X.shape)

plt.figure()
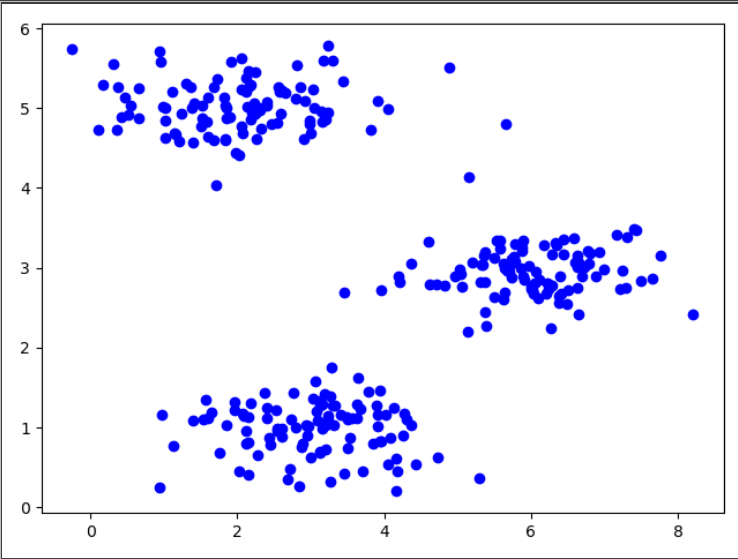
plt.scatter(X[:,],X[:,],c='b',marker="o")
plt.show()

注意：对于我们的无监督学习中，训练集中是没有标签值的，所以只有X，没有y

二：归类---寻找每个训练样本的聚类中心

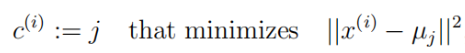
（一）代码实现

def find_closest_centroids(X,centroids):
    m = X.shape[0]
    idx = np.zeros(m)   #记录每个训练样本距离最短聚类中心最短的索引
    idx = idx.astype(int)   #因为numpy中没有int、float类型，是由系统决定是32、或者64位大小。所以我们这里手动设置位int类型，为后面做准备

    for i in range(m):
        idx[i] = np.argmin(np.sum(np.power((centroids-X[i]),2),1))  #先计算各个中心到该点的平方和距离，返回最小的索引

    return idx

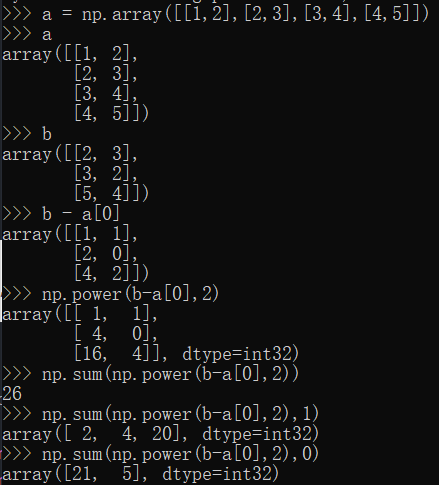
（二）补充矩阵减去向量、np.sum的使用

（三）结果测试

k =   # 设置聚簇中心个数为3
initial_centroids = np.array([[, ], [, ], [, ]]) #手动初始化三个聚类中心点
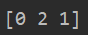
idx = find_closest_centroids(X,initial_centroids)
print(idx[:])

三：根据上一步归类结果---更新聚簇中心位置

（一）代码实现

def compute_centroids(X,idx,K):
    (m,n)=X.shape
    centroids_new = np.zeros((k,n))

    #进行更新操作，用每个聚类中心所有点的位置平均值作为新的聚类中心位置
    for i in range(K):
        centroids_new[i] = np.mean(X[np.where(idx==i)[0],0)    #按列求均值

    return  centroids_new

（二）回顾np.where操作

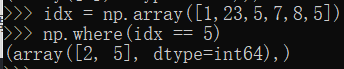
注意：我们这里np.where返回的是一个元组类型，我们如果想要获取内部数据，应该使用np.where(idx == 5)[0]可以获取np.array类型数据

（三）结果测试

data = sio.loadmat("ex7data2.mat")
X = data['X']

k =   # 设置聚簇中心个数为3
initial_centroids = np.array([[, ], [, ], [, ]]) #手动初始化三个聚类中心点
idx = find_closest_centroids(X,initial_centroids)

c_n = compute_centroids(X,idx,k)
print(c_n)

四：实现K-mean算法

（一）代码实现

def run_k_means(X,init_centroids,max_iters=):
    m,n = X.shape
    idx = np.zeros(m)
    k = init_centroids.shape[]
    centroids = init_centroids

    #开始迭代
    if max_iters != :
        for i in range(max_iters):  #按迭代次数进行迭代
            idx = find_closest_centroids(X,centroids)
            centroids = compute_centroids(X,idx,k)
    else:
        while True: #直到连续两次的迭代结果都是一样的，就返回
            idx = find_closest_centroids(X, init_centroids)
            centroids = compute_centroids(X,idx,k)
            if (init_centroids == centroids).all():
                break
            init_centroids = centroids

    return idx,centroids

（二）结果显示

data = sio.loadmat("ex7data2.mat")
X = data['X']

k =   # 设置聚簇中心个数为3
initial_centroids = np.array([[, ], [, ], [, ]]) #手动初始化三个聚类中心点

max_iters =
idx, centroids = run_k_means(X,initial_centroids,max_iters)
#获取各个聚簇信息
cluster_1 = X[np.where(idx==0)[0],:]
cluster_2 = X[np.where(idx==1)[0],:]
cluster_3 = X[np.where(idx==2)[0],:]

#绘制图像
plt.figure()
plt.scatter(cluster_1[:,],cluster_1[:,],c='r',marker="o")
plt.scatter(cluster_2[:,],cluster_2[:,],c='b',marker="o")
plt.scatter(cluster_3[:,],cluster_3[:,],c='g',marker="o")
plt.show()

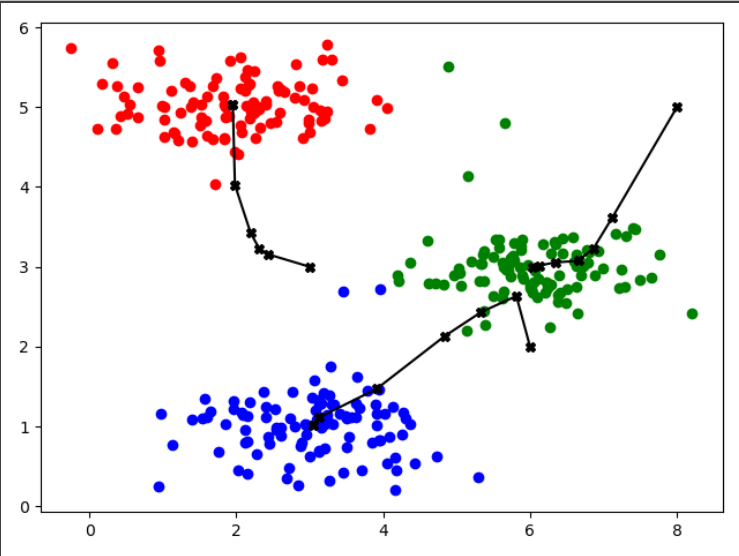
（三）改进版---绘制聚簇中心移动轨迹

def run_k_means(X,init_centroids,max_iters=):
    m,n = X.shape
    idx = np.zeros(m)
    k = init_centroids.shape[]
    centroids = init_centroids
    cent_rec = init_centroids   #记录中心移动信息

    #开始迭代
    if max_iters != :
        for i in range(max_iters):  #按迭代次数进行迭代
            idx = find_closest_centroids(X,centroids)
            centroids = compute_centroids(X,idx,k)
            cent_rec = np.append(cent_rec,centroids,axis=)  #记录中心移动信息,按列添加
    else:
        while True: #直到连续两次的迭代结果都是一样的，就返回
            idx = find_closest_centroids(X, init_centroids)
            centroids = compute_centroids(X,idx,k)
            if (init_centroids == centroids).all():
                break
            init_centroids = centroids
            cent_rec = np.append(cent_rec,centroids,axis=)  #记录中心移动信息,按列添加

    return idx,centroids,cent_rec

data = sio.loadmat("ex7data2.mat")
X = data['X']

k =   # 设置聚簇中心个数为3
initial_centroids = np.array([[, ], [, ], [, ]]) #手动初始化三个聚类中心点

max_iters =
idx, centroids, cent_rec = run_k_means(X,initial_centroids,max_iters)

#获取各个聚簇信息
cluster_1 = X[np.where(idx==)[],:]
cent_1 = cent_rec[].reshape(-,)
cluster_2 = X[np.where(idx==)[],:]
cent_2 = cent_rec[].reshape(-,)
cluster_3 = X[np.where(idx==)[],:]
cent_3 = cent_rec[].reshape(-,)

#绘制图像
plt.figure()
plt.scatter(cluster_1[:,],cluster_1[:,],c='r',marker="o")
plt.plot(np.array(cent_1[:,]),np.array(cent_1[:,]),c='black',marker="X")
plt.scatter(cluster_2[:,],cluster_2[:,],c='b',marker="o")
plt.plot(np.array(cent_2[:,]),np.array(cent_2[:,]),c='black',marker="X")
plt.scatter(cluster_3[:,],cluster_3[:,],c='g',marker="o")
plt.plot(np.array(cent_3[:,]),np.array(cent_3[:,]),c='black',marker="X")
plt.show()

五：随机初始化聚类中心函数

在运行 K-均值算法的之前，我们首先要随机初始化所有的聚类中心点。

（一）重点回顾

注意点一：

（1）应该把聚类中心的数值K设置为比训练样本数量m小的值；

（2）随机挑选K个训练样本；

（3）设定μ1,...,μk，让它们等于这K个样本。

注意点二：

避免局部最优：如果想让找到最优可能的聚类，可以尝试多次随机初始化，以此来保证能够得到一个足够好的结果，选取代价最小的一个也就是代价函数J最小的。事实证明，在聚类数K较小的情况下（2~10个），使用多次随机初始化会有较大的影响，而如果K很大的情况，多次随机初始化可能并不会有太大效果。

（二）代码实现

def kmeans_init_centroids(X,k):　　#随机获取聚类中心
    centroids = np.zeros((k,X.shape[]))

    #随机选取训练样本个数
    idx = np.random.choice(X.shape[],k)
    centroids = X[idx,:]

    return centroids

def comp_J(X,centroids,idx):    #计算代价，计算平方和，不进行开方
    # 获取各个聚簇信息
    cluster_1 = X[np.where(idx == )[], :]
    cluster_2 = X[np.where(idx == )[], :]
    cluster_3 = X[np.where(idx == )[], :]

    #计算代价
    J_1 = np.sum(np.power(cluster_1-centroids[],))
    J_2 = np.sum(np.power(cluster_2-centroids[],))
    J_3 = np.sum(np.power(cluster_3-centroids[],))

    return J_1+J_2+J_3

def kmeans_run(X,k,rand_iter,max_iters=):　　#进行多次计算代价，然后选取最小的
    min_J = -
    idx_res = np.zeros(X.shape[])
    centroids_res = np.zeros((k,X.shape[]))
    cent_rec_res = centroids_res

    for i in range(rand_iter):
        init_centroids = kmeans_init_centroids(X,k)
        idx, centroids, cent_rec = run_k_means(X,init_centroids,max_iters)
        #计算代价
        if min_J < :
            min_J = comp_J(X,centroids,idx)
        else:
            new_J = comp_J(X,centroids,idx)
            # print(new_J)
            if new_J < min_J:
                idx_res, centroids_res, cent_rec_res = idx, centroids, cent_rec
    # print(min_J)
    return idx_res, centroids_res, cent_rec_res

data = sio.loadmat("ex7data2.mat")
X = data['X']

k =   # 设置聚簇中心个数为3
rand_iter = 

max_iters =
idx, centroids, cent_rec = kmeans_run(X,k,rand_iter,max_iters)

idx, centroids, cent_rec = run_k_means(X,kmeans_init_centroids(X,k),max_iters)
# print(comp_J(X,centroids,idx))  #266.65851965491936
#获取各个聚簇信息
cluster_1 = X[np.where(idx==)[],:]
cent_1 = cent_rec[].reshape(-,)
cluster_2 = X[np.where(idx==)[],:]
cent_2 = cent_rec[].reshape(-,)
cluster_3 = X[np.where(idx==)[],:]
cent_3 = cent_rec[].reshape(-,)

#绘制图像
plt.figure()
plt.scatter(cluster_1[:,],cluster_1[:,],c='r',marker="o")
plt.plot(np.array(cent_1[:,]),np.array(cent_1[:,]),c='black',marker="X")
plt.scatter(cluster_2[:,],cluster_2[:,],c='b',marker="o")
plt.plot(np.array(cent_2[:,]),np.array(cent_2[:,]),c='black',marker="X")
plt.scatter(cluster_3[:,],cluster_3[:,],c='g',marker="o")
plt.plot(np.array(cent_3[:,]),np.array(cent_3[:,]),c='black',marker="X")
plt.show()

补充：我们可以认为每个点的特征就是x_1,x_2,而我们的聚类中心就是由x_1和x_2组成的。

--------------------------K-Means算法进行图像压缩--------------------------

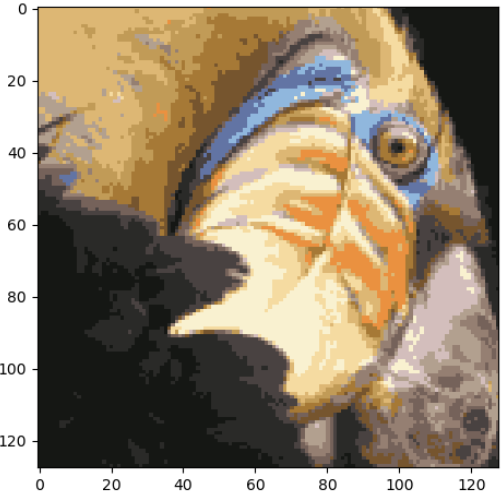
使用K-Means进行图像压缩。我们使用聚类来找到最具代表性的少数颜色，并使用聚类分配讲原始的24位颜色，映射到较低维的颜色空间

一：数据读取

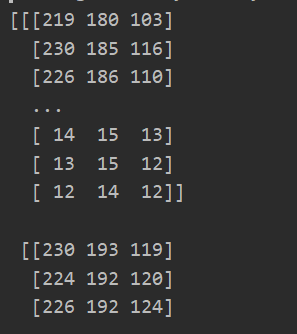
image_data = sio.loadmat("bird_small.mat")
data = image_data['A']
print(data)
print(data.shape)

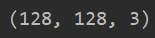
二：数据预处理

#数据归一化  因为每个数据都是0-255之间
data = data /
data = np.reshape(data,(data.shape[]*data.shape[],data.shape[]))
print(data.shape)

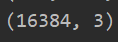
注意：我们的特征就是颜色空间三通道，所以我们后面求取的聚类中心就是我们找到的最具代表的颜色空间

三:获取我们的聚类中心（同之前）

（一）代码实现

def find_closest_centroids(X,centroids):
    m = X.shape[]
    idx = np.zeros(m)   #记录每个训练样本距离最短聚类中心最短的索引
    idx = idx.astype(int)   #因为numpy中没有int、float类型，是由系统决定是32、或者64位大小。所以我们这里手动设置位int类型，为后面做准备

    for i in range(m):
        idx[i] = np.argmin(np.sum(np.power((centroids-X[i]),),))  #先计算各个中心到该点的平方和距离，返回最小的索引

    return idx

def compute_centroids(X,idx,K):
    (m,n)=X.shape
    centroids_new = np.zeros((k,n))

    #进行更新操作，用每个聚类中心所有点的位置平均值作为新的聚类中心位置
    for i in range(K):
        centroids_new[i] = np.mean(X[np.where(idx==i)[]],)    #按列求均值

    return centroids_new

def run_k_means(X,init_centroids,max_iters=):
    m,n = X.shape
    idx = np.zeros(m)
    k = init_centroids.shape[]
    centroids = init_centroids

    #开始迭代
    if max_iters != :
        for i in range(max_iters):  #按迭代次数进行迭代
            idx = find_closest_centroids(X,centroids)
            centroids = compute_centroids(X,idx,k)
    else:
        while True: #直到连续两次的迭代结果都是一样的，就返回
            idx = find_closest_centroids(X, init_centroids)
            centroids = compute_centroids(X,idx,k)
            if (init_centroids == centroids).all():
                break
            init_centroids = centroids

    return idx,centroids

def kmeans_init_centroids(X,k):
    centroids = np.zeros((k,X.shape[]))

    #随机选取训练样本个数
    idx = np.random.choice(X.shape[],k)
    centroids = X[idx,:]

    return centroids

（二）获取压缩结果

image_data = sio.loadmat("bird_small.mat")
data = image_data['A']
#数据归一化  因为每个数据都是0-255之间
data = data /
X = np.reshape(data,(data.shape[]*data.shape[],data.shape[]))
k =
max_iters = 

#随机初始化聚类中心
init_centroids = kmeans_init_centroids(X,k)
#获取聚类中心
idx,centroids = run_k_means(X,init_centroids,max_iters)
#将所有数据点，设置归属到对应的聚类中心去
idx = find_closest_centroids(X,centroids)
#将每一个像素值与聚类结果进行匹配
X_recovered = centroids[idx,:]  #将属于一个聚类的像素，设置为聚类中心的值（统一）

print(X_recovered.shape)    #(, )

X_recovered = np.reshape(X_recovered,(data.shape[],data.shape[],data.shape[]))　　#再展开为三维数据

补充：使用索引扩展矩阵

（三）压缩结果显示

plt.figure()
plt.imshow(data)    #显示原始图像
plt.show()

plt.figure()
plt.imshow(X_recovered) #显示压缩后的图像
plt.show()

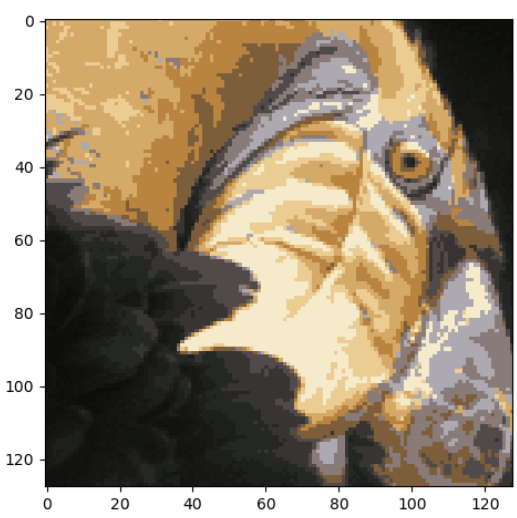
当k=6时：

四：补充使用sklearn库进行K-means算法使用

import numpy as np
import matplotlib.pyplot as plt
import scipy.io as sio
from sklearn.cluster import KMeans

image_data = sio.loadmat("bird_small.mat")
data = image_data['A']
#数据归一化  因为每个数据都是0-255之间
data = data /
X = np.reshape(data,(data.shape[]*data.shape[],data.shape[]))

model = KMeans(n_clusters=16,n_init=100,n_jobs=-1)  #n_init设置获取初始簇中心的更迭次数，防止局部最优 n_jobs设置并行（使用CPU数，-1则使用所有CPU）
model.fit(X)    #开始聚类

centroids = model.cluster_centers_  #获取聚簇中心
C = model.predict(X) #获取每个数据点的对应聚簇中心的索引

X_recovered = centroids[C].reshape((data.shape[],data.shape[],data.shape[])) #获取新的图像

plt.figure()
plt.imshow(data)    #显示原始图像
plt.show()

plt.figure()
plt.imshow(X_recovered) #显示压缩后的图像
plt.show()

参数讲解：https://blog.csdn.net/sinat_26917383/article/details/70240628