Cup HDU - 2289

题目传送门：https://vjudge.net/problem/HDU-2289

题意：有一个上口小于底部的圆台形水杯，告诉我们水的体积求水高度。

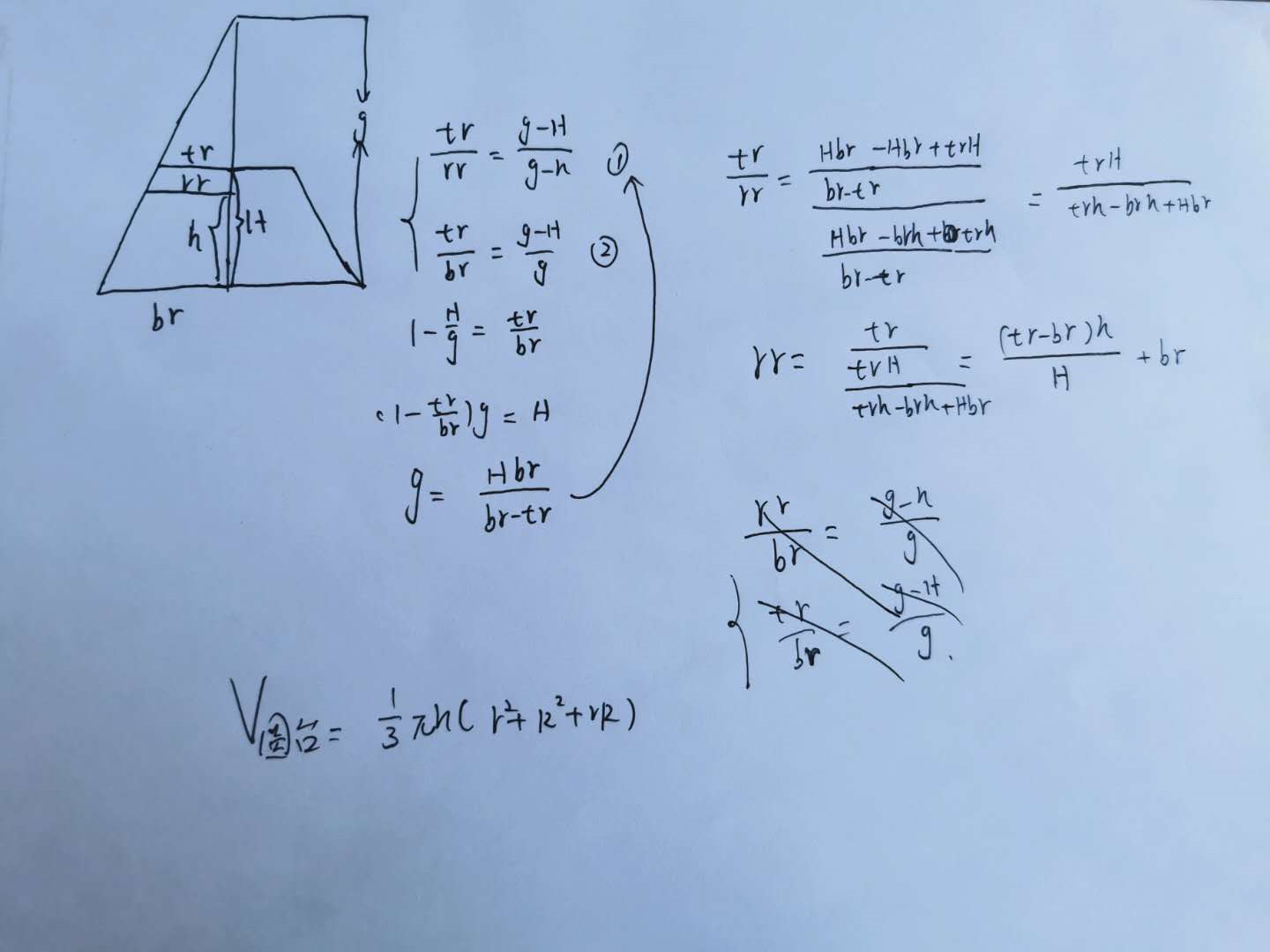
思路：利用高中数学知识求rr然后二分求h，具体化简过程见下图。

  1 //#include<bits/stdc++.h>
  2 #include<time.h>
  3 #include <set>
  4 #include <map>
  5 #include <stack>
  6 #include <cmath>
  7 #include <queue>
  8 #include <cstdio>
  9 #include <string>
 10 #include <vector>
 11 #include <cstring>
 12 #include <utility>
 13 #include <cstring>
 14 #include <iostream>
 15 #include <algorithm>
 16 #include <list>
 17 using namespace std;
 18 #define eps 1e-10
 19 #define PI acos(-1.0)
 20 #define lowbit(x) ((x)&(-x))
 21 #define zero(x) (((x)>0?(x):-(x))<eps)
 22 #define mem(s,n) memset(s,n,sizeof s);
 23 #define ios {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);}
 24 typedef long long ll;
 25 typedef unsigned long long ull;
 26 const int maxn=1e3+5;
 27 const int Inf=0x7f7f7f7f;
 28 const ll Mod=999911659;
 29 const int N=3e3+5;
 30 bool isPowerOfTwo(int n) { return n > 0 && (n & (n - 1)) == 0; }//判断一个数是不是 2 的正整数次幂
 31 int modPowerOfTwo(int x, int mod) { return x & (mod - 1); }//对 2 的非负整数次幂取模
 32 int getBit(int a, int b) { return (a >> b) & 1; }// 获取 a 的第 b 位，最低位编号为 0
 33 int Max(int a, int b) { return b & ((a - b) >> 31) | a & (~(a - b) >> 31); }// 如果 a>=b,(a-b)>>31 为 0，否则为 -1
 34 int Min(int a, int b) { return a & ((a - b) >> 31) | b & (~(a - b) >> 31); }
 35 ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
 36 ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
 37 int Abs(int n) {
 38   return (n ^ (n >> 31)) - (n >> 31);
 39   /* n>>31 取得 n 的符号，若 n 为正数，n>>31 等于 0，若 n 为负数，n>>31 等于 -1
 40      若 n 为正数 n^0=n, 数不变，若 n 为负数有 n^(-1)
 41      需要计算 n 和 -1 的补码，然后进行异或运算，
 42      结果 n 变号并且为 n 的绝对值减 1，再减去 -1 就是绝对值 */
 43 }
 44 ll binpow(ll a, ll b,ll c) {
 45   ll res = 1;
 46   while (b > 0) {
 47     if (b & 1) res = res * a%c;
 48     a = a * a%c;
 49     b >>= 1;
 50   }
 51   return res%c;
 52 }
 53 void extend_gcd(ll a,ll b,ll &x,ll &y)
 54 {
 55     if(b==0) {
 56         x=1,y=0;
 57         return;
 58     }
 59     extend_gcd(b,a%b,x,y);
 60     ll tmp=x;
 61     x=y;
 62     y=tmp-(a/b)*y;
 63 }
 64 ll mod_inverse(ll a,ll m)
 65 {
 66     ll x,y;
 67     extend_gcd(a,m,x,y);
 68     return (m+x%m)%m;
 69 }
 70 ll eulor(ll x)
 71 {
 72    ll cnt=x;
 73    ll ma=sqrt(x);
 74    for(int i=2;i<=ma;i++)
 75    {
 76     if(x%i==0) cnt=cnt/i*(i-1);
 77     while(x%i==0) x/=i;
 78    }
 79    if(x>1) cnt=cnt/x*(x-1);
 80    return cnt;
 81 }
 82 double br,tr,H,v;
 83 double getv(double h)
 84 {
 85     double rr=(tr-br)*h/H+br;
 86     return PI*h*(br*br+br*rr+rr*rr)/3;
 87 }
 88 int main()
 89 {
 90     int t;
 91     cin>>t;
 92     while(t--)
 93     {
 94         cin>>br>>tr>>H>>v;
 95        double l=0,r=H,mid;
 96        while(r-l>eps)
 97        {
 98            mid=(l+r)/2;
 99            if(fabs(getv(mid)-v)<=eps) break;
100            else if(fabs((getv(mid)))>v) r=mid;
101            else l=mid;
102        }
103        printf("%.6f\n",mid);
104     }
105     return 0;
106 }