【bzoj 4455】小星星（树型DP+容斥原理+dfs建树和计算的2种方式）

题意：给一个n个点的图和一个n个点的树，求图和树上的点一一对应的方案数。（N<=17)

解法：
1.在树的结构上进行tree DP，f[i][j]表示树上点 i 对应图上点 j 时，这个点所在子树的方案数。O(n^3)。

2.我们可以发现如果按这个定义进行DP，“一 一对应”的关系挺难保证。若枚举出全排列得到对应关系，这样就C(n,n)=n! 只能拿到暴力分；那么我们就不限制“一 一对应”而改为“一对多”的关系进行tree DP，利用容斥原理达到O(2^n)的复杂度。（P.S.至于为什么用容斥原理我也不清楚，待我弄懂之后我会再更新的。    2个月后的今天 我说：“应该不会有更新了......”≡[。。]≡）

3.这题的容斥原理应用是这样的：用二进制数枚举出每次DP有哪些数没有对应的树上的点，将所有情况下的DP方案数之和按求补集的公式来求就是“所有数都一一对应树上的点”的答案。

下图中圆圈1表示数1没有对应的点的方案数，依次类推。有颜色部分是我们要求的补集。

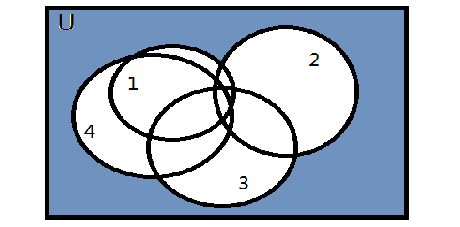
下面附上代码——

  1 #include<cstdio>
  2 #include<cstdlib>
  3 #include<cstring>
  4 #include<iostream>
  5 using namespace std;
  6
  7 typedef long long LL;
  8 const int N=20,M=400;
  9 struct node{int x,y,next;}a[2*N];
 10 int last[N],len;
 11 bool v[N][N],vis[N];
 12 LL f[N][N];
 13 int b[N],bt;
 14
 15 void add(int x,int y)
 16 {
 17     len++;
 18     a[len].x=x,a[len].y=y;
 19     a[len].next=last[x],last[x]=len;
 20 }
 21
 22 void dfs(int x,int fa)
 23 {
 24     /*for(int k=last[x];k;k=a[k].next)
 25     {
 26       int y=a[k].y;
 27       if(y==fa)continue;
 28       dfs(y,x);
 29     }
 30     for (int kk=1;kk<=bt;kk++)
 31     {
 32       int i=b[kk];
 33       f[x][i]=1;
 34       for (int k=last[x];k;k=a[k].next)
 35       {
 36         int y=a[k].y;
 37         if (y==fa) continue;
 38         LL h=0;
 39         for (int kkk=1;kkk<=bt;kkk++)
 40         {
 41           int j=b[kkk];
 42           if (v[i][j]) h+=f[y][j];
 43         }
 44         f[x][i]*=h;
 45       }
 46     }*///边建树，边不重复地DP
 47     if (vis[x]) return;
 48     for (int kk=1;kk<=bt;kk++)
 49     {
 50       int i=b[kk];
 51       f[x][i]=1;
 52       for (int k=last[x];k;k=a[k].next)
 53       {
 54         int y=a[k].y;
 55         if (y==fa) continue;
 56         dfs(y,x);
 57         vis[y]=true;
 58         LL h=0;
 59         for (int kkk=1;kkk<=bt;kkk++)
 60         {
 61           int j=b[kkk];
 62           if (v[i][j]) h+=f[y][j];
 63         }
 64         f[x][i]*=h;
 65       }
 66     }//打标记，快一点
 67 }
 68
 69 int main()
 70 {
 71     int n,m;
 72     scanf("%d%d",&n,&m);
 73     memset(v,false,sizeof(v));
 74     for (int i=1;i<=m;i++)
 75     {
 76       int x,y;
 77       scanf("%d%d",&x,&y);
 78       v[x][y]=v[y][x]=true;
 79     }
 80     memset(last,0,sizeof(last));
 81     len=0;
 82     for (int i=1;i<n;i++)
 83     {
 84       int x,y;
 85       scanf("%d%d",&x,&y);
 86       add(x,y),add(y,x);
 87     }
 88     LL ans=0;
 89     for (int i=1;i<(1<<n);i++)
 90     {
 91       bt=0;
 92       for (int j=1;j<=n;j++)
 93         if (i&(1<<(j-1))) b[++bt]=j;
 94       memset(vis,false,sizeof(vis));
 95       dfs(1,0);
 96       LL h=0;
 97       for (int j=1;j<=bt;j++)
 98         h+=f[1][b[j]];
 99       if ((n-bt)%2==0) ans+=h;//按补集
100       else ans-=h;
101     }
102     printf("%lld\n",ans);
103     return 0;
104 }