CF 1912 A NEKO's Maze Game

题目传送门

题目描述

输入

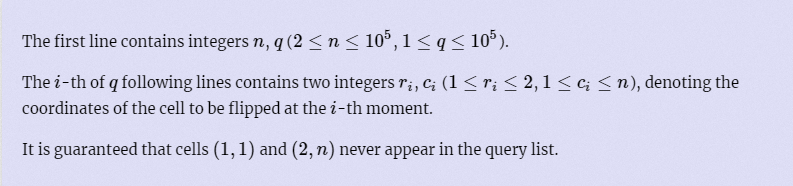
输出

样例

样例输入

样例输出

Yes
No
No
No
Yes

一句话题意：2*n的迷宫，从（1，1）出发到（2，n），初始时全部的都是地面，每次询问会把一个地面给变成熔浆，熔浆变成地面，熔浆不能通过，问是否可以走到。

分析

我们先开一个a数组存储每个方格当前的状态，0表示地面，1表示熔岩

在一个长度为n，宽度为2的迷宫中，有三种情况不能从（1，1）走到（2，n）

情况一

0	1	0	0	0
0	1	0	0	0

情况二

0	1	0	0	0
0	0	1	0	0

情况三

0	0	1	0	0
0	1	0	0	0

情况一：a[1][n]和a[2][n]同时为1

情况二：a[1][n]和a[2][n+1]同时为1 或 a[2][n]和a[1][n+1]同时为1

情况三：a[1][n]和a[2][n-1]同时为1 或 a[2][n]和a[1][n-1]同时为1

在其他情况下，总能通过别的点到达（2，n）

如果我们一个一个去枚举的话，那么1e5的数据肯定会超时

所以我们可以记录一下以上三种情况出现的次数，当次数不为0时，输出No，否则输出Yes

写代码的时候再考虑一下边界问题就可以了

代码

 #include<cstdio>
 #include<cmath>
 #include<algorithm>
 #include<iostream>
 #include<cstring>
 using namespace std;
 const int maxn=1e5+;
 int ans=;
 int a[][maxn];
 int main(){
     int n,q;
     scanf("%d%d",&n,&q);
     for(int i=;i<=q;i++){
         int aa,bb;
         scanf("%d%d",&aa,&bb);
         if(a[aa][bb]==){
             a[aa][bb]=;
             if(aa==){
                 if(a[][bb]==) ans--;
                 if(a[][bb+]== && bb+<=n) ans--;
                 if(a[][bb-]== && bb>) ans--;
             } else {
                 if(a[][bb]==) ans--;
                 if(a[][bb+]== && bb+<=n) ans--;
                 if(a[][bb-]== && bb>) ans--;
             }//如果这个点是由岩浆变成地面的话，之前算出来的ans就要更新
             //因为之前形成断路的地方现在不一定还有断路
             if(ans==) printf("Yes\n");
             else printf("No\n");
         } else {
             a[aa][bb]=;
             if(aa==){
                 if(a[][bb]==) ans++;
                 if(a[][bb+]== && bb+<=n) ans++;//bb+1<=n防止超出边界
                 if(a[][bb-]== && bb>) ans++;//bb>1防止超出边界
             } else {
                 if(a[][bb]==) ans++;
                 if(a[][bb+]== && bb+<=n) ans++;
                 if(a[][bb-]== && bb>) ans++;
             }
             //如果这个点是由地面变成岩浆的话，之前算出来的ans就要更新
             //因为之前没有断路的地方现在可能会有断路
             if(ans==) printf("Yes\n");
             else printf("No\n");
         }
     }
     return ;
 }

这个代码不是很优秀，但是比较直观

如果你已经理解的话，我们可以把代码进一步简化

优化

首先是空间上的优化，我们可以开一个2*1e5的数组，将原来的两行分别用k和！k表示，跟我们写的滚动数组方法类似

其次我们可以不必要写太多判断，有些判断合并就可以

最后我们可以删去一些不必要的头文件，再用一些位运算，使代码更加简洁高效

代码

 #include<bits/stdc++.h>
 using namespace std;
 const int maxn=1e5+;
 int a[][maxn],q,ans=,n,x,y;//ans记录不能联通的区域的个数
 int main(){
     scanf("%d%d",&n,&q);
     while(q--){
         scanf("%d%d",&x,&y);
         x--;//x--,方便以后的!运算 ,就是把原本的1和2变成了0和1
         a[x][y]^=;//改变这个位置的状态 ,1^1=0,0^1=1
         int m=a[x][y]*-;//如果是0就是可以走，那结果就要减，1的话加
         ans+=m*(a[!x][y-]+a[!x][y]+a[!x][y+]);//进行ans的累加
         if(ans==) printf("Yes\n");
         else printf("No\n");
     }
     return ;
 }

比较

时间上虽然差不多，但内存和长度减少了不少，看代码也更清晰

最重要的是，这样写思维可以提升上去，不然那么容易过了也没什么意思