PAT/简单模拟习题集（二）

B1018. 锤子剪刀布 (20)

Discription：

大家应该都会玩“锤子剪刀布”的游戏：两人同时给出手势，胜负规则如图所示：

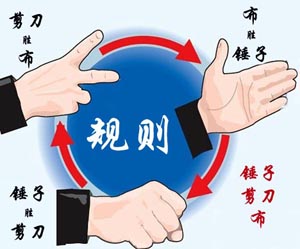
现给出两人的交锋记录，请统计双方的胜、平、负次数，并且给出双方分别出什么手势的胜算最大。

Input：

输入第1行给出正整数N（<=10⁵），即双方交锋的次数。随后N行，每行给出一次交锋的信息，即甲、乙双方同时给出的的手势。C代表“锤子”、J代表“剪刀”、B代表“布”，第1个字母代表甲方，第2个代表乙方，中间有1个空格。

Output：

输出第1、2行分别给出甲、乙的胜、平、负次数，数字间以1个空格分隔。第3行给出两个字母，分别代表甲、乙获胜次数最多的手势，中间有1个空格。如果解不唯一，则输出按字母序最小的解。

Sample Input：

10
C J
J B
C B
B B
B C
C C
C B
J B
B C
J J

Sample Output：

5 3 2
2 3 5
B B

 #include <cstdio>

 #define MaxSize 3

 int ListA[MaxSize], ListB[MaxSize], Time[MaxSize];

 int main()

 {

     //freopen("E:\\Temp\\input.txt", "r", stdin);

     int N;

     char c1, c2;

     scanf("%d", &N);

     for(int i=; i<N; i++) {

         getchar();

         scanf("%c %c", &c1, &c2);

             if(c1 == 'B') {

                 if(c2 == 'B') {

                     Time[]++;

                 } else if(c2 == 'C') {

                     Time[]++;

                     ListA[]++;

                 } else {

                     Time[]++;

                     ListB[]++;

                 }

             } else if(c1 == 'C') {

                 if(c2 == 'B') {

                     Time[]++;

                     ListB[]++;

                 } else if(c2 == 'C') {

                     Time[]++;

                 } else {

                     Time[]++;

                     ListA[]++;

                 }

             } else {

                 if(c2 == 'B') {

                     Time[]++;

                     ListA[]++;

                 } else if(c2 == 'C') {

                     Time[]++;

                     ListB[]++;

                 } else {

                     Time[]++;

                 }

             }

     }

     printf("%d %d %d\n%d %d %d\n", Time[], Time[], Time[], Time[], Time[], Time[]);

     if(ListA[] >= ListA[]) {

         if(ListA[] >= ListA[])

             printf("B ");

         else

             printf("J ");

     } else {

         if(ListA[] >= ListA[])

             printf("C ");

         else

             printf("J ");

     }

     if(ListB[] >= ListB[]) {

         if(ListB[] >= ListB[])

             printf("B\n");

         else

             printf("J\n");

     } else {

         if(ListB[] >= ListB[])

             printf("C\n");

         else

             printf("J\n");

     }

     return ;

 }

 #include <cstdio>

 int change(char c)

 {

     if(c == 'B')

         return ;

     else if(c == 'C')

         return ;

     else

         return ;

 }

 int main()

 {

     //freopen("E:\\Temp\\input.txt", "r", stdin);

     char mp[] = {'B', 'C', 'J'};

     int n;

     scanf("%d", &n);

     int times_A[] = {}, times_B[] = {};

     int hand_A[] = {}, hand_B[] = {};

     char c1, c2;

     int k1, k2;

     for(int i=; i<n; i++) {

         getchar();

         scanf("%c %c", &c1, &c2);

         k1 = change(c1);

         k2 = change(c2);

         if((k1+)% == k2) {

             times_A[]++;

             times_B[]++;

             hand_A[k1]++;

         } else if(k1 == k2) {

             times_A[]++;

             times_B[]++;

         } else {

             times_A[]++;

             times_B[]++;

             hand_B[k2]++;

         }

     }

     printf("%d %d %d\n", times_A[], times_A[], times_A[]);

     printf("%d %d %d\n", times_B[], times_B[], times_B[]);

     int id1 = , id2 = ;

     for(int i=; i<; i++) {

         if(hand_A[i] > hand_A[id1])

             id1 = i;

         if(hand_B[i] > hand_B[id2])

             id2 = i;

     }

     printf("%c %c\n", mp[id1], mp[id2]);

     return ;

 }

A1042. Shuffling Machine (20)

Description：

Shuffling is a procedure used to randomize a deck of playing cards. Because standard shuffling techniques are seen as weak, and in order to avoid "inside jobs" where employees collaborate with gamblers by performing inadequate shuffles, many casinos employ automatic shuffling machines. Your task is to simulate a shuffling machine.

The machine shuffles a deck of 54 cards according to a given random order and repeats for a given number of times. It is assumed that the initial status of a card deck is in the following order:

S1, S2, ..., S13, H1, H2, ..., H13, C1, C2, ..., C13, D1, D2, ..., D13, J1, J2

where "S" stands for "Spade", "H" for "Heart", "C" for "Club", "D" for "Diamond", and "J" for "Joker". A given order is a permutation of distinct integers in [1, 54]. If the number at the i-th position is j, it means to move the card from position i to position j. For example, suppose we only have 5 cards: S3, H5, C1, D13 and J2. Given a shuffling order {4, 2, 5, 3, 1}, the result will be: J2, H5, D13, S3, C1. If we are to repeat the shuffling again, the result will be: C1, H5, S3, J2, D13.

Input：

Each input file contains one test case. For each case, the first line contains a positive integer K (<= 20) which is the number of repeat times. Then the next line contains the given order. All the numbers in a line are separated by a space.

Output：

For each test case, print the shuffling results in one line. All the cards are separated by a space, and there must be no extra space at the end of the line.

Sample Input：

2
36 52 37 38 3 39 40 53 54 41 11 12 13 42 43 44 2 4 23 24 25 26 27 6 7 8 48 49 50 51 9 10 14 15 16 5 17 18 19 1 20 21 22 28 29 30 31 32 33 34 35 45 46 47

Sample Output：

S7 C11 C10 C12 S1 H7 H8 H9 D8 D9 S11 S12 S13 D10 D11 D12 S3 S4 S6 S10 H1 H2 C13 D2 D3 D4 H6 H3 D13 J1 J2 C1 C2 C3 C4 D1 S5 H5 H11 H12 C6 C7 C8 C9 S2 S8 S9 H10 D5 D6 D7 H4 H13 C5

 #include <cstdio>

 #define MaxSize 55

 int List1[MaxSize], List2[MaxSize], List3[MaxSize];

 int main()

 {

     //freopen("E:\\Temp\\input.txt", "r", stdin);

     int N, temp;

     scanf("%d", &N);

     for(int i=; i<MaxSize; i++) {

         List1[i] = i;

         scanf("%d", &List2[i]);

     }

     for(int i=; i<N; i++) {

         for(int j=; j<MaxSize; j++) {

             List3[List2[j]] = List1[j];

         }

         for(int k=; k<MaxSize; k++) {

             List1[k] = List3[k];

         }

     }

     for(int i=; i<MaxSize-; i++) {

         if(List1[i] > ) {

             printf("J%d ", List1[i]-);

         } else if(List1[i] > ) {

             printf("D%d ", List1[i]-);

         } else if(List1[i] > ) {

             printf("C%d ", List1[i]-);

         } else if(List1[i] > ) {

             printf("H%d ", List1[i]-);

         } else {

             printf("S%d ", List1[i]);

         }

     }

     if(List1[MaxSize-] > ) {

         printf("J%d\n", List1[MaxSize-]-);

     } else if(List1[MaxSize-] > ) {

         printf("D%d\n", List1[MaxSize-]-);

     } else if(List1[MaxSize-] > ) {

         printf("C%d\n", List1[MaxSize-]-);

     } else if(List1[MaxSize-] > ) {

         printf("H%d\n", List1[MaxSize-]-);

     } else {

         printf("S%d\n", List1[MaxSize-]);

     }

     return ;

 }

 #include <cstdio>

 const int N = ;

 char mp[] = {'S', 'H', 'C', 'D', 'J'};

 int start[N], end[N], next[N];

 int main()

 {

     //freopen("E:\\Temp\\input.txt", "r", stdin);

     int K;

     scanf("%d", &K);

     for(int i=; i<=N; i++)

         start[i] = i;

     for(int i=; i<=N; i++)

         scanf("%d", &next[i]);

     for(int step = ; step < K; step++) {

         for(int i=; i<=N; i++)

             end[next[i]] = start[i];

         for(int i=; i<=N; i++)

             start[i] = end[i];

     }

     for(int i=; i<=N; i++) {

         if(i != )

             printf(" ");

         start[i]--;

         printf("%c%d", mp[start[i]/], start[i]%+);

     }

     return ;

 }

A1046.Shortest Distance (20)

Description：

The task is really simple: given N exits on a highway which forms a simple cycle, you are supposed to tell the shortest distance between any pair of exits.

Input：

Each input file contains one test case. For each case, the first line contains an integer N (in [3, 10⁵]), followed by N integer distances D₁ D₂ ... D_N, where D_i is the distance between the i-th and the (i+1)-st exits, and D_N is between the N-th and the 1st exits. All the numbers in a line are separated by a space. The second line gives a positive integer M (<=10⁴), with M lines follow, each contains a pair of exit numbers, provided that the exits are numbered from 1 to N. It is guaranteed that the total round trip distance is no more than 10⁷.

Output：

For each test case, print your results in M lines, each contains the shortest distance between the corresponding given pair of exits.

Sample Input：

5 1 2 4 14 9
3
1 3
2 5
4 1

Sample Output：

 #include <cstdio>

 #include <algorithm>

 using namespace std;

 const int MAXN = ;

 int dis[MAXN], A[MAXN];

 int main()

 {

     int sum = , query, n, left, right;

     scanf("%d", &n);

     for(int i=; i<=n; i++) {

         scanf("%d", &A[i]);

         sum += A[i];

         dis[i] = sum;

     }

     scanf("%d", &query);

     for(int i=; i<query; i++) {

         scanf("%d%d", &left, &right);

         if(left > right)

             swap(left, right);

         int temp = dis[right-]-dis[left-];

         printf("%d\n", min(temp, sum-temp));

     }

     return ;

 }

A1065. A+B and C (64bit) (20)

Description：

Given three integers A, B and C in [-2⁶³, 2⁶³], you are supposed to tell whether A+B > C.

Input：

The first line of the input gives the positive number of test cases, T (<=10). Then T test cases follow, each consists of a single line containing three integers A, B and C, separated by single spaces.

Ouput：

For each test case, output in one line "Case #X: true" if A+B>C, or "Case #X: false" otherwise, where X is the case number (starting from 1).

Sample Input：

3
1 2 3
2 3 4
9223372036854775807 -9223372036854775808 0

Output：

Case #1: false
Case #2: true
Case #3: false

 #include <cstdio>

 int main()

 {

     //freopen("E:\\Temp\\input.txt", "r", stdin);

     int T, tcase = ;

     scanf("%d", &T);

     while(T--) {

         long long a, b, c;

         scanf("%lld%lld%lld", &a, &b, &c);

         long long res = a+b;

         bool flag;

         if(a> && b> && res<)

             flag = true;

         else if(a< && b< && res>=)

             flag = false;

         else if(res > c)

             flag = true;

         else

             flag = false;

         if(flag == true)

             printf("Case #%d: true\n", tcase++);

         else

             printf("Case #%d: false\n", tcase++);

     }

     return ;

 }

B1010. 一元多项式求导 (25)

Description：

设计函数求一元多项式的导数。（注：xⁿ（n为整数）的一阶导数为n*x^n-1。）

Input：

以指数递降方式输入多项式非零项系数和指数（绝对值均为不超过1000的整数）。数字间以空格分隔。

Output：

以与输入相同的格式输出导数多项式非零项的系数和指数。数字间以空格分隔，但结尾不能有多余空格。注意“零多项式”的指数和系数都是0，但是表示为“0 0”。

Sample Input：

3 4 -5 2 6 1 -2 0

Sample Output：

12 3 -10 1 6 0

 #include <cstdio>

 int main()

 {

     //freopen("E:\\Temp\\input.txt", "r", stdin);

     int a[] = {};

     int k, e, counter = ;

     while(scanf("%d%d", &k, &e) != EOF) {

         a[e] = k;

     }

     a[] = ;

     for(int i=; i<=; ++i) {

         a[i-] = a[i]*i;

         a[i] = ;

         if(a[i-] != )

             counter++;

     }

     if(counter == )

         printf("0 0\n");

     else {

         for(int i=; i>=; --i) {

             if(a[i] != ) {

                 printf("%d %d", a[i], i);

                 counter--;

                 if(counter != )

                     printf(" ");

             }

         }

     }

     return ;

 }

A1002. A+B for Polynomials (25)

Description：

This time, you are supposed to find A+B where A and B are two polynomials.

Input：

Each input file contains one test case. Each case occupies 2 lines, and each line contains the information of a polynomial: K N1 a_N1 N2 a_N2 ... NK a_NK, where K is the number of nonzero terms in the polynomial, Ni and a_Ni (i=1, 2, ..., K) are the exponents and coefficients, respectively. It is given that 1 <= K <= 10，0 <= NK < ... < N2 < N1 <=1000.

Output：

For each test case you should output the sum of A and B in one line, with the same format as the input. Notice that there must be NO extra space at the end of each line. Please be accurate to 1 decimal place.

Sample Input：

2 1 2.4 0 3.2
2 2 1.5 1 0.5

Sample Output：

3 2 1.5 1 2.9 0 3.2

 #include <cstdio>

 #define MaxSize 1010

 double List[MaxSize];

 int main()

 {

     //freopen("E:\\Temp\\input.txt", "r", stdin);

     int K, expon, counter = ;

     double coef;

     scanf("%d", &K);

     for(int i=; i<K; ++i) {

         scanf("%d %lf", &expon, &coef);

         List[expon] += coef;

     }

     scanf("%d", &K);

     for(int i=; i<K; ++i) {

         scanf("%d %lf", &expon, &coef);

         List[expon] += coef;

     }

     for(int i=; i<MaxSize; ++i) {

         if(List[i] != )

             ++counter;

     }

     printf("%d", counter);

     for(int i=MaxSize-; i>=; --i) {

         if(List[i] != ) {

             printf(" %d %.1f", i, List[i]);

         }

     }

     return ;

 }

A1009. Product of Polynomials (25)

Description：

This time, you are supposed to find A*B where A and B are two polynomials.

Input：

Output：

For each test case you should output the product of A and B in one line, with the same format as the input. Notice that there must be NO extra space at the end of each line. Please be accurate up to 1 decimal place.

Sample Input：

2 1 2.4 0 3.2
2 2 1.5 1 0.5

Sample Output：

3 3 3.6 2 6.0 1 1.6

 #include <cstdio>

 #define MaxSize 2010

 double List1[MaxSize], List2[MaxSize];

 int main()

 {

     //freopen("E:\\Temp\\input.txt", "r", stdin);

     int K, expon, counter = ;

     double coef;

     scanf("%d", &K);

     for(int i=; i<K; ++i) {

         scanf("%d %lf", &expon, &coef);

         List1[expon] += coef;

     }

     scanf("%d", &K);

     for(int i=; i<K; ++i) {

         scanf("%d %lf", &expon, &coef);

         for(int j=; j<MaxSize; j++)

             List2[expon+j] += List1[j]*coef;

     }

     for(int i=; i<MaxSize; ++i) {

         if(List2[i] != )

             ++counter;

     }

     printf("%d", counter);

     for(int i=MaxSize-; i>=; --i) {

         if(List2[i] != )

             printf(" %d %.1f", i, List2[i]);

     }

     return ;

 }

 #include <cstdio>

 struct Poly {

     int exp;

     double cof;

 }poly[];

 double ans[];

 int main()

 {

     int n, m, number = ;

     scanf("%d", &n);

     for(int i=; i<n; ++i)

         scanf("%d %lf", &poly[i].exp, &poly[i].cof);

     scanf("%d", &m);

     for(int i=; i<m; ++i) {

         int exp;

         double cof;

         scanf("%d %lf", &exp, &cof);

         for(int j=; j<n; j++)

             ans[exp+poly[j].exp] += (cof*poly[j].cof);

     }

     for(int i=; i<=; ++i) {

         if(ans[i] != )

             ++number;

     }

     printf("%d", number);

     for(int i=; i>=; --i) {

         if(ans[i] != )

             printf(" %d %.1f", i, ans[i]);

     }

     return ;

 }

PAT/简单模拟习题集（二）的更多相关文章

PAT/简单模拟习题集（一）
B1001.害死人不偿命的(3n+1)猜想 (15) Description: 卡拉兹(Callatz)猜想: 对任何一个自然数n,如果它是偶数,那么把它砍掉一半:如果它是奇数,那么把(3n+1)砍掉 ...
java web学习总结(二十二) -------------------简单模拟SpringMVC
在Spring MVC中,将一个普通的java类标注上Controller注解之后,再将类中的方法使用RequestMapping注解标注,那么这个普通的java类就够处理Web请求,示例代码如下: ...
JavaWeb学习总结(四十九)——简单模拟Sping MVC
在Spring MVC中,将一个普通的java类标注上Controller注解之后,再将类中的方法使用RequestMapping注解标注,那么这个普通的java类就够处理Web请求,示例代码如下: ...
(hdu step 8.1.6)士兵队列训练问题(数据结构，简单模拟——第一次每2个去掉1个,第二次每3个去掉1个.知道队伍中的人数<=3，输出剩下的人 )
题目: 士兵队列训练问题 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total ...
spring之mvc原理分析及简单模拟实现
在之前的一篇博客中已经简单的实现了spring的IOC和DI功能,本文将在之前的基础上实现mvc功能. 一什么是MVC MVC简单的说就是一种软件实现的设计模式,将整个系统进行分层,M(model ...
C++笔记（7）——一些模拟题：简单模拟、查找元素、图形输出、日期处理、进制转换、字符串处理
以下内容基本来自<算法笔记>,作者为胡凡,建议直接买书看,我这里只是摘抄部分当笔记,不完整的. 简单模拟就是一类"题目怎么说你就怎么做"的题目.这类题目不涉及算法,只 ...
sort回调的简单模拟
本来是准备讲CPP中的std::sort,但因为最近Java用得多,不知怎么的便习惯性走Java角度看问题了,所以这篇文章看起来估计会有点奇怪... 一.简单模拟sort回调 std::sort函数本 ...
WPF简单模拟QQ登录背景动画
介绍之所以说是简单模拟,是因为我不知道QQ登录背景动画是怎么实现的.这里是通过一些办法把它简化了,做成了类似的效果效果图大体思路首先把背景看成是一个4行8列的点的阵距,X轴Y轴都是距离70.把 ...
Linux 内核链表的简单模拟（2）
接上一篇Linux 内核链表的简单模拟(1) 第五章:Linux内核链表的遍历 /** * list_for_each - iterate over a list * @pos: the & ...

随机推荐

HTTP 错误 403.14–Forbidden错误解决
运行环境:开发环境:Windows7旗舰版64bit.VisualStudio2008 With SP1.ArcEngine10.0.NetFrameWork4.0.IIS7和C#开发语言. 问题描述 ...
HR开发 SuccessFactors与HCM数据映射
SuccessFactors Employee Central ----->> HCM 增强点 ES_PAOCF_EC_TOOLS HCM ----->> SuccessFac ...
引用模板中的类型时，切记要加上typename声明！！
如题,发现实际操作中太容易忘记了,导致一些莫名其妙的编译错误,故在此记录!
Linux常用命令笔记一
笔记1:查看ubuntu是32位还是64位的方法及其版本号查看ubuntu是64还是32的命令如下: uname -m 如果是i386到i686,那就是32位系统:如果是x86_64 ,那就是64系 ...
Ubuntu 16 安装odoo10 实录
安装Ubuntu 16,省略安装时,默认用户名为 odoo ubuntu 16开始使用 systemd 管理服务,但是systemd 兼容 sysv init 脚本下载 odoo源码从 htt ...
ASP.NET c# textbox 正则表达式文本框只允许输入数字（验证控件RegularExpressionValidator ）
<input type="text" name="test" onKeyUp="test1.value=(this.value=this.val ...
ZOJ3774_Power of Fibonacci
求fibonacci数列前N个数的K次方和. 通项公式:F[n]=((1+sqrt(5))/sqrt(5)-(1-sqrt(5))/sqrt(5))/sqrt(5). 有点乱,不过由于可以保证最后的结 ...
Three ways to set specific DeviceFamily XAML Views in UWP
Three ways to set specific DeviceFamily XAML Views in UWP http://igrali.com/2015/08/02/three-ways-to ...
Android应用程序Monkey测试
Monkey是Android SDK中附带的一个测试工具:Monkey用于进行压力测试,软件开发人员结合monkey打印日志和系统日志,解决测试中出现的问题. Monkey测试的特点:所有事件都是随机 ...
51nod 1428 活动安排问题(优先队列)
1428 活动安排问题首先按照开始时间从小到大排序. 其实只要维护一个结束时间的最小堆,每次比较开始时间和堆中最小时间的大小,如果比它大就放入堆中并且时间就要变成当前任务的结束时间, 否则就要新开一 ...

PAT/简单模拟习题集（二）

PAT/简单模拟习题集（二）的更多相关文章

随机推荐

热门专题