常见的DP优化类型

常见的DP优化类型

1单调队列直接优化

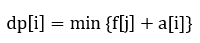
如果a[i]单调增的话，显然可以用减单调队列直接存f[j]进行优化。

2斜率不等式

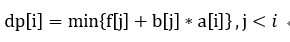
即实现转移方程中的i,j分离。b单调减，a单调增（可选）。

令：

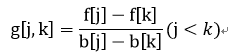
在队首，如果g[j,k]>=-a[i]，那么j优于k，而且以后j也优于k，因此k可以重队列中直接删去。在队尾，如果x<y<z,且g[x,y]<=g[y,z]，也就是说只要y优于x一定可以得出z优于y的，我们就删去y。

经过队尾的筛选，我们在队列中得到的是一个斜率递减的下凸包，每次寻找从上往下被-a[i]斜率的线所扫到的第一个点，a[i]单调的话通过队首的维护我们可以在均摊O(1)的时间内找到这个点。值得注意的是，即使a[i]不单调，我们仍然可以通过二分在O(log n)的时间内找到转移点。

高维的场合和低维并没有区别。只要使用斜率和单调队列优化，一定可以降一维。高维时可以没有j<i的限制，这时我们理解成若干条b[j]*x+f[j]的直线形成一个下凸包求值器，然后带入一个a[i]作为x计算得的结果就是答案，时间是O(nlogn)。

3下凸包求值器(CF-455E)

这是一种很奇怪的情况。有些时候，问题可以转化成给定一堆直线K[i]*X+B[i]，每次询问选择连续的一段[a..b]和一个x，求最小值。

做法是构造一个下凸包求值器，实现对给定x求值和合并两个功能，内部实现是按K排好序的线段序列。然后线段树每个节点维护一个求值器。这样可以在O(nlognlogn)的时间内解决问题。

4分治优化

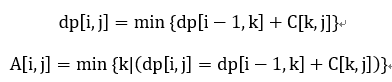
元素的分组合并问题通常拥有以上的形式。优化的条件是A[i,j]的单调性，也就是说A[i,j]<=A[i,j+1]。也即要求C[k,j]满足四边形不等式C[a,c]+C[b,d]<=C[a,d]+C[b,c] 。（含义是：越晚并入新元素，并入的组尺寸越小，其额外代价越小。这里四边形不等式已经是充分条件了，不需要区间单调）

优化的伪代码如下：

compute(i,l,r,ol,or)

1. 令m=(l+r)>>1

2. 寻找k=ol..or,使得dp[i,m]=dp[i-1,k]+C[k,m]最小

3. 如果l==r，返回。否则执行compute(i,l,m-1,ol,k);compute(i,m+1,r,k,or);

5四边形不等式

四边形不等式优化应用于区间DP：

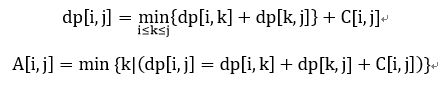
要求C[i,j]满足四边形不等式C[a,c]+C[b,d]<=C[a,d]+C[b,c]和区间单调性C[b,c]<=C[a,d]。注意这里的C不在转移方程的内部，而是一个定值。

满足上件的前提下，有A[i,j-1]<=A[i,j]<=A[i+1,j]（关键条件），因此可以优化。优化方法为以|i-j|的递增顺序DP，同时记录各个A[i,j]值，枚举时在A[i,j-1]和A[i+1,j]的区间卡内枚举。

6矩阵优化

一眼能看出来就是快速幂。多为期望或概率DP。

7线段树优化

通常是有不确定的强制转移的场合。如FAFU1231。

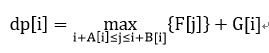
此时因A[i],B[i]欠缺单调性，单调队列的使用受到限制，用线段树即可解决。如斜率优化中掺杂此种限制，则同上3.