BZOJ 1855 股票交易 - 单调队列优化dp

传送门

题目分析：

\(f[i][j]\)表示第i天，手中拥有j份股票的最优利润。

• 如果不买也不卖，那么$$f[i][j] = f[i-1][j]$$
• 如果买入，那么$$f[i][j] = max{f[i - w - 1][k] - A_p*(j - k)} (j - as + 1 \le k \le j)$$由于是从小的更新大的，所以顺序
• 如果卖出，那么$$f[i][j] = max{f[i - w - 1][k] + B_p*(k - j)} (j \le k \le j + bs - 1)$$由于是从大更新小的，所以倒序
  
  现在已经得到了一个\(n^3\)转移的方法，现在来考虑如何优化成\(n^2\)。
  
  
  
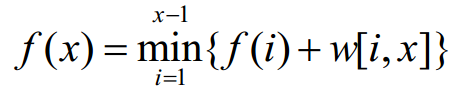
  形如这样的方程，具有决策单调性，可以使用单调队列优化。将上面推得的后两个方程整理得

\[f[i][j] = max\{(f[i - w - 1][k] + A_p * k) - A_p * j\}
\]

\[f[i][j] = max\{(f[i - w - 1][k] + B_p * k) - B_p *j)\}
\]

中间括号前的用单调队列维护单调性，每次插入时更新决策。

code

#include<bits/stdc++.h>
using namespace std;
const int N = 2005, OO = 0x3f3f3f3f;
int n, w, maxp;
int f[N][N], ans;
typedef pair<int, int> P;
P que[N];
struct node{
	int ap, bp, as, bs;
}d[N];

int main(){
	scanf("%d%d%d", &n, &maxp, &w);
	for(register int i = 1; i <= n; i++)
		scanf("%d%d%d%d", &d[i].ap, &d[i].bp, &d[i].as, &d[i].bs);
	memset(f, -OO, sizeof f);
	for(register int i = 1; i <= n; i++){
		for(register int j = 0; j <= d[i].as; j++) f[i][j] = -d[i].ap * j;   //初始化为只买股票
		for(register int j = 0; j <= maxp; j++) f[i][j] = max(f[i][j], f[i - 1][j]);
		if(i - w - 1 >= 0){
			register int head = 1, tail = 0;
			for(register int j = 0; j <= maxp; j++){     //从小的转移，顺序
				while(head <= tail && que[head].first < j - d[i].as) head++;
				while(head <= tail && que[tail].second <= f[i - w - 1][j] + d[i].ap * j) tail--;
				que[++tail] = P(j, f[i - w - 1][j] + d[i].ap * j);
				if(head <= tail) f[i][j] = max(f[i][j], que[head].second - d[i].ap * j);
			}
			head = 1, tail = 0;
//			for(int j = 0; j <= maxp; j++){             //错误
			for(register int j = maxp; j >= 0; j--){    //从大的转移，倒序
				while(head <= tail && que[head].first > j + d[i].bs) head++;
				while(head <= tail && que[tail].second <= f[i - w - 1][j] + d[i].bp * j) tail--;
				que[++tail] = P(j, f[i - w - 1][j] + d[i].bp * j);
				if(head <= tail) f[i][j] = max(f[i][j], que[head].second - d[i].bp * j);
			}
		}
	}
	printf("%d", f[n][0]);
	return 0;
}