umi 调试

最近在umi.  设置一个layout字段， 结果左边菜单栏就出现了。 很神奇。 决定对这个库一探究竟。

我是一个喜欢看底层库的人，网上所有的启动方式都是yarn或者npm start 启动服务。然后在浏览器运行调试的。 这个调试的是前端。

我想调试的是后端。 通过跟踪，发现其实

yarn start  调用的是 umi dev

umi  是一个软连接到umi.js的文件

#!/usr/bin/env node

const resolveCwd = require('resolve-cwd');

const { name, bin } = require('../package.json');
const localCLI = resolveCwd.silent(`${name}/${bin['umi']}`);
const b = !process.env.USE_GLOBAL_UMI && localCLI && localCLI !== __filename;
if (b) {
  const debug = require('@umijs/utils').createDebug('umi:cli');
  debug('Using local install of umi');
  console.log(`localCLI:${localCLI}`);
  require(localCLI);
} else {
  require('../lib/cli');
}

也就是其实执行的umi/lib/cli.js文件,  关键部分代码

_asyncToGenerator(function* () {
  try {
    switch (args._[0]) {
      case 'dev':
        const child = (0, _fork.default)({
          scriptPath: require.resolve('./forkedDev')
        }); // ref:
        // http://nodejs.cn/api/process/signal_events.html

        process.on('SIGINT', () => {
          child.kill('SIGINT');
        });
        process.on('SIGTERM', () => {
          child.kill('SIGTERM');
        });
        break;

也就是fork的forkedDev文件

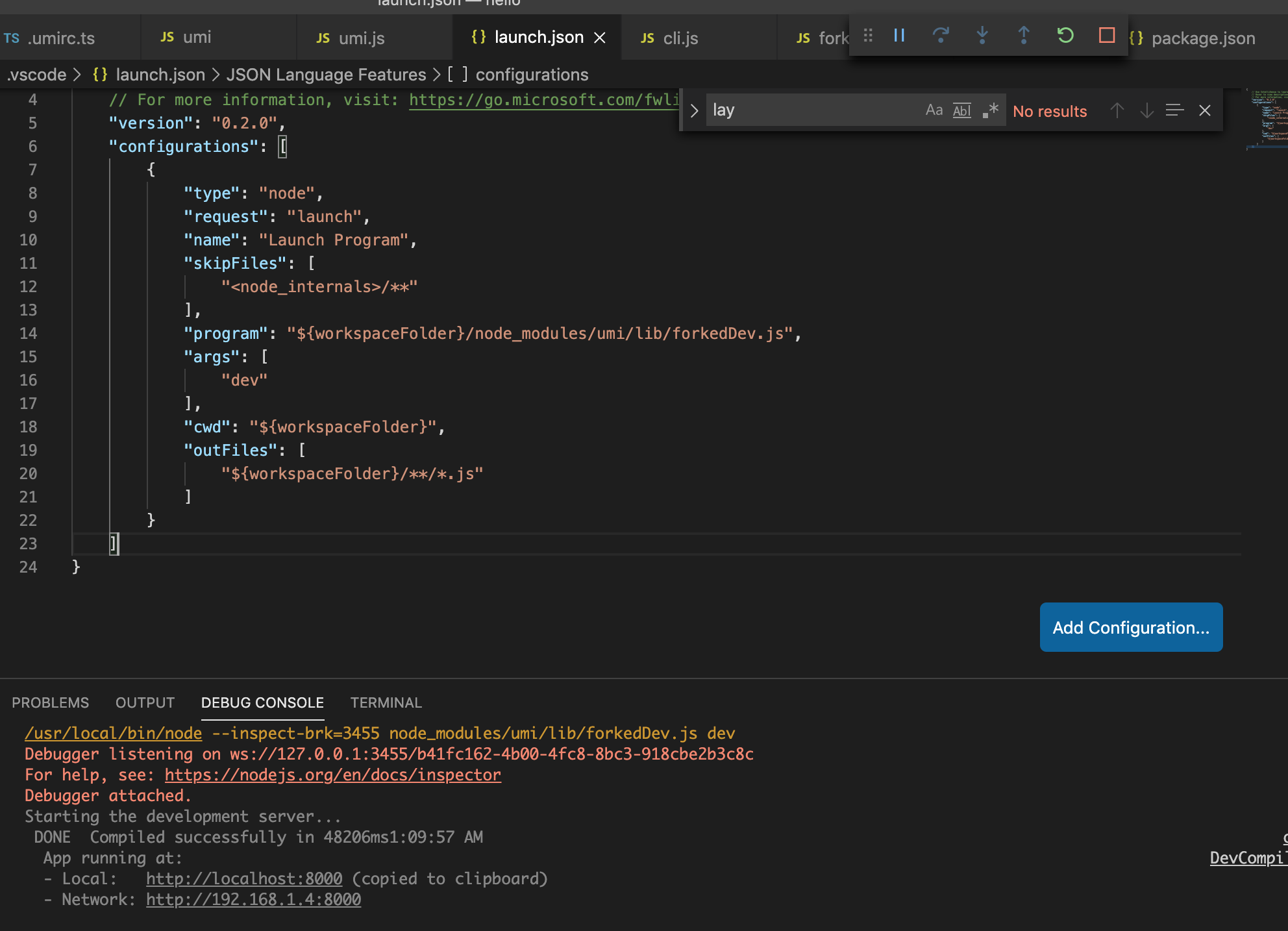
于是就有了vscode的调试配置文件。launch.json

{
    // Use IntelliSense to learn about possible attributes.
    // Hover to view descriptions of existing attributes.
    // For more information, visit: https://go.microsoft.com/fwlink/?linkid=830387
    "version": "0.2.0",
    "configurations": [
        {
            "type": "node",
            "request": "launch",
            "name": "Launch Program",
            "skipFiles": [
                "<node_internals>/**"
            ],
            "program": "${workspaceFolder}/node_modules/umi/lib/forkedDev.js",
            "args": [
                "dev"
            ],
            "cwd": "${workspaceFolder}",
            "outFiles": [
                "${workspaceFolder}/**/*.js"
            ]
        }
    ]
}

　　可以调试umi服务端了。