差分数组&&定义&&使用方法&&与线段树的区别

**1.定义**
对于一个有n个元素的数组a[n]，我们令a[i]-a[i-1]=d[i],且d[1]=a[1]-0=a[1];那么我们将d[i]称为**差分数组**---即记录数组中的每项元素与前一项的差值

**2.性质**
(1)计算数组a各项的值（数组下标从1开始，a[0]=0）
例如a[3]=d[3]+d[2]+d[1]
=（a[3]-a[2]）+（a[2]-a[1]）+（a[1]-a[0]）
=a[3]

(2)统计d数组的前缀和sum数组
什么是前缀和？前缀和顾名思义就是**前面i个数的总和**
sum[i]=d[1]+d[2]+....d[i]=a[1]+a[2]-a[1]+.....a[i]-a[i-1]=a[i]；

**3.用法**
（1）快速处理区间加减操作
每次在区间[l,r]增减x只需要令d[l]+x,d[r+1]-x，就可以保证[l,r]增加了x，而对[1,l-1]和[r+1,n]无影响。复杂度则是O(n)的。这样我们不必对区间内每一个数进行处理，只需处理两个差分后的数即可.

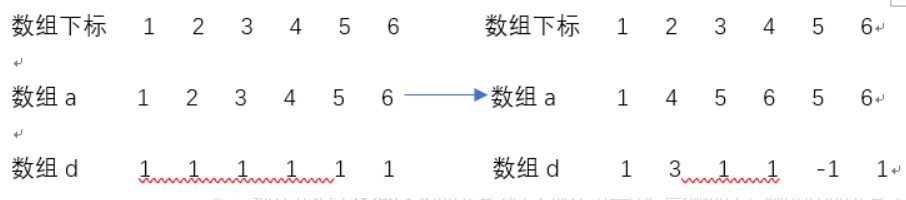
现在我们令区间[2,4]的元素都+2,那么第一个受影响的差分数组中的元素为d[2],因为d[2]=a[2]-a[1],a[2]是区间内第一个变化的元素，所以**第一个受影响**的差分数组元素是d[2],同理最后一个受影响的是d[5],即d[r+1]（你看a[4]+2，d[5]=a[5]-a[4]的值变小了）
我们令d[2]+2,令d[5]-2,就相当于对整个区间的元素进行了+2操作，避免了对数组a所有元素进行操作。那么为什么不用对差分数组d[3],d[4]进行修改呢，因为区间内的元素同时都加上同样的数字，***所以d[3],d[4]计算后仍然是不变的***
**那么我们就可以得到a[2]=sum[2]=d[1]+d[2]=4;a[4]=sum[4]=1+3+1+1=6;a[5]=sum[5]=1+3+1+1-1=5;**
(2)**询问区间和问题**
区间[L,R]的和为sum[R]-sum[L-1];
**ps:这里的sum数组和前面的差分数组的前缀和数组不是一个东西，这里代表区间和，例如sum[3]=a[1]+a[2]+a[3]**
**4.和线段树的区别**
差分数组：
更新时间复杂度 O(1)
查询时间复杂度 O(n)
线段树 ：
更新时间复杂度 O(logn)
查询时间复杂度 O(logn)
建树时间复杂度O(n)
因此，差分数组适用于多次更新，常量次查询，数据范围在**1e7**以内的情况；线段树适用于多次更新，多次查询，数据范围在**1e5**以内的情况。
下面例题的要求比较低，两种数据结构都可以用。
but如果改动一下要求：
1、数据范围不是1e5而是1e7，只能用差分数组。
2、不是一次查询而是多次查询，只能用线段树。

相关问题：
[Color the ball HDU - 1556 ](https://vjudge.net/problem/HDU-1556)
问题描述：
N个气球排成一排，从左到右依次编号为1,2,3....N.每次给定2个整数a b(a <= b),lele便为骑上他的“小飞鸽"牌电动车从气球a开始到气球b依次给每个气球涂一次颜色。但是N次以后lele已经忘记了第I个气球已经涂过几次颜色了，你能帮他算出每个气球被涂过几次颜色吗？
每个测试实例第一行为一个整数N,(N <= 100000).接下来的N行，每行包括2个整数a b(1 <= a <= b <= N)。
当N = 0，输入结束。
每个测试实例输出一行，包括N个整数，第I个数代表第I个气球总共被涂色的次数。
Sample Input
3
1 1
2 2
3 3
3
1 1
1 2
1 3
0
Sample Output
1 1 1
3 2 1
区间修改查询问题一般会想到用线段树或者树状数组来做，但是这题的特点就是多次修改，最后只有一次查询，属于离线查询，即**完成修改后再查询**，因此可以用到差分数组.

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 #include<cstring>
 using namespace std;
 ;
 int d[maxn],sum[maxn];
 int main()
 {
 　　ios_base::sync_with_stdio(); cin.tie(); cout.tie();
 　　int n;
 while(cin>>n){
 　　)break;
 　　memset(d,,sizeof(d));
,sizeof(sum));
 　　int l,r;
 　　;i<=n;i++){
 　　　　cin>>l>>r;//在一个区间内加x，只需要在差分数组上面d[l]+x,d[r+1]-x就可以了
 　　　　d[l]+=;
 　　　　d[r+]-=;
 　　}
 　　;i<=n;i++){
 　　　　sum[i]=sum[i-]+d[i];
 　　}
 　　;i<n;i++)cout<<sum[i]<<" ";
 　　　　cout<<sum[n]<<endl;
 　　}

 ;
 }

参考博客 :
https://www.cnblogs.com/COLIN-LIGHTNING/p/8436624.html
https://www.cnblogs.com/robin1998/p/6863402.html
https://blog.csdn.net/Nothing_but_Fight/article/details/90340695#commentsedit