BAPC K题 Keep Him Inside

Problem Statement：

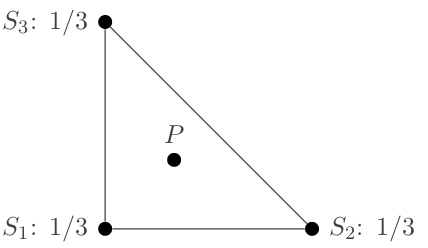
As a result of a long-standing war between the Sorcerers and the Orcs, you have been assigned as officer of one of the prison blocks. Recently the leader of the Orcs has been captured and placed inside a special cell. It works as follows: the cell is a convex polygon with at every vertex a guard tower in which a Sorcerer is placed.

Thanks to the recent agreement between the Sorcerers and Orcs, called the Beneficial Activities for Prisoners in Cells, the leader of the Orcs should be able to move around freely in his cell. You do not want your prisoner to escape, so you order the sorcerers to work together on a containment spell. If done right, this creates a magical aura around the prisoner that will prevent him from escaping.

In order for the containment spell to work, all Sorcerers need to channel a certain fraction of their maximum power into the spell such that two things hold:

• The spell needs to be perfectly balanced: the sum of the fractions of power over all Sorcerers must equal 1.
• The centre of the spell should coincide with the prisoner. This means that the average of the positions of Sorcerers, weighted by the fraction of power they are channeling, should be the location of the prisoner.

Given the layout of the cell and the location of the prisoner, assign a fraction of power each

Sorcerer should spend so that the containment spell works.

Input

• The first line contains 3 ≤ n ≤ 10，the number of Sorcerers in guard towers and two

  integers -10⁴ ≤ x,y ≤ 10⁴, the coordinates of the prisoner.

• Then follow n lines, each of which contains two integers -10⁴ ≤ x,y ≤ 10⁴ , the coordinates of a Sorcerer.

It is guaranteed that the locations are given in counter clockwise order and form a strictly convex polygon, i.e. no three points lie on a line. The prisoner is located strictly inside the polygon.

Output

• Output n lines where the ith line contains a floating point number between 0 and 1inclusive: the fraction of power that the ith Sorcerer should use for the containment spell to work.

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e4+;
ll xa,xb,xc,ya,yb,yc,px,py;
double a,b,c,ans[maxn];
int n;
struct node //用来记录巫师所在点的坐标
{
ll x,y;
}no[];
int main()
{
cin >> n >> px >> py;   //px,py表示P点的坐标
for(int i =  ; i < n ; i++)
cin >> no[i].x >> no[i].y;
xc = no[].x,yc = no[].y;
xb = no[].x,yb = no[].y;
px -= xc,py -= yc;
xb -= xc,yb -= yc;
for(int i =  ; i < n ; i++)
{
xa = xb,ya = yb;
xb = no[i].x,yb = no[i].y;
xb -= xc,yb -= yc;
double f = xb*ya - xa*yb;//表示上述公式中a，b前面的系数
a = (xb*py - px*yb)/f;
b = (px*ya - py*xa)/f;
c =  - a - b;
if(a >=  && b >=  && c >= )//要保证计算出的权值全为正，并记录在ans中
{
ans[] = c; //c对应的是x3也就是这里的xc，对应点的下标为0
ans[i-] = a; //a对应的是x1也就是这里的xa，对应点的下标为i-1
ans[i] = b; //b对应的是x2也就是这里的xb，对应点的下标为i
}
}
for(int i =  ; i < n ; i++)
cout << setprecision() << ans[i] << endl;
return ;
}