关联规则之Aprior算法

关联规则挖掘在电商、零售、大气物理、生物医学已经有了广泛的应用，本篇文章将介绍一些基本知识和Aprori算法。

　啤酒与尿布的故事已经成为了关联规则挖掘的经典案例，还有人专门出了一本书《啤酒与尿布》，虽然说这个故事是哈弗商学院杜撰出来的，但确实能很好的解释关联规则挖掘的原理。我们这里以一个超市购物篮迷你数据集来解释关联规则挖掘的基本概念：

TID	Items
T1	{牛奶,面包}
T2	{面包,尿布,啤酒,鸡蛋}
T3	{牛奶,尿布,啤酒,可乐}
T4	{面包,牛奶,尿布,啤酒}
T5	{面包,牛奶,尿布,可乐}

　一、关联规则、自信度、自持度的定义 　　表中的每一行代表一次购买清单（注意你购买十盒牛奶也只计一次，即只记录某个商品的出现与否）。数据记录的所有项的集合称为总项集，上表中的总项集S={牛奶,面包,尿布,啤酒,鸡蛋,可乐}。

　　关联规则就是有关联的规则，形式是这样定义的：两个不相交的非空集合X、Y，如果有X-->Y，就说X-->Y是一条关联规则。举个例子，在上面的表中，我们发现购买啤酒就一定会购买尿布，{啤酒}-->{尿布}就是一条关联规则。关联规则的强度用支持度(support)和自信度(confidence)来描述，

　　支持度的定义：support(X-->Y) = |X交Y|/N=集合X与集合Y中的项在一条记录中同时出现的次数/数据记录的个数。例如：support({啤酒}-->{尿布}) = 啤酒和尿布同时出现的次数/数据记录数 = 3/5=60%。

　　自信度的定义：confidence(X-->Y) = |X交Y|/|X| = 集合X与集合Y中的项在一条记录中同时出现的次数/集合X出现的个数 。例如：confidence({啤酒}-->{尿布}) = 啤酒和尿布同时出现的次数/啤酒出现的次数=3/3=100%;confidence({尿布}-->{啤酒}) = 啤酒和尿布同时出现的次数/尿布出现的次数 = 3/4 = 75%。

　　这里定义的支持度和自信度都是相对的支持度和自信度，不是绝对支持度，绝对支持度abs_support = 数据记录数N*support。

　　支持度和自信度越高，说明规则越强，关联规则挖掘就是挖掘出满足一定强度的规则。

二、关联规则挖掘的定义与步骤

　　关联规则挖掘的定义：给定一个交易数据集T，找出其中所有支持度support >= min_support、自信度confidence >= min_confidence的关联规则。

　　有一个简单而粗鲁的方法可以找出所需要的规则，那就是穷举项集的所有组合，并测试每个组合是否满足条件，一个元素个数为n的项集的组合个数为2^n-1(除去空集)，所需要的时间复杂度明显为O(2^N)，对于普通的超市，其商品的项集数也在1万以上，用指数时间复杂度的算法不能在可接受的时间内解决问题。怎样快速挖出满足条件的关联规则是关联挖掘的需要解决的主要问题。

　　仔细想一下，我们会发现对于{啤酒-->尿布}，{尿布-->啤酒}这两个规则的支持度实际上只需要计算{尿布，啤酒}的支持度，即它们交集的支持度。于是我们把关联规则挖掘分两步进行：

　　1）生成频繁项集

　　这一阶段找出所有满足最小支持度的项集，找出的这些项集称为频繁项集。

　　2）生成规则

　　在上一步产生的频繁项集的基础上生成满足最小自信度的规则，产生的规则称为强规则。

　　关联规则挖掘所花费的时间主要是在生成频繁项集上，因为找出的频繁项集往往不会很多，利用频繁项集生成规则也就不会花太多的时间，而生成频繁项集需要测试很多的备选项集，如果不加优化，所需的时间是O(2^N)。

三、Apriori定律

　　为了减少频繁项集的生成时间，我们应该尽早的消除一些完全不可能是频繁项集的集合，Apriori的两条定律就是干这事的。

　　Apriori定律1)：如果一个集合是频繁项集，则它的所有子集都是频繁项集。举例：假设一个集合{A,B}是频繁项集，即A、B同时出现在一条记录的次数大于等于最小支持度min_support，则它的子集{A},{B}出现次数必定大于等于min_support，即它的子集都是频繁项集。

　　Apriori定律2)：如果一个集合不是频繁项集，则它的所有超集都不是频繁项集。举例：假设集合{A}不是频繁项集，即A出现的次数小于min_support，则它的任何超集如{A,B}出现的次数必定小于min_support，因此其超集必定也不是频繁项集。

　　利用这两条定律，我们抛掉很多的候选项集，Apriori算法就是利用这两个定理来实现快速挖掘频繁项集的。

四、Apriori算法

　　Apriori是由a priori合并而来的，它的意思是后面的是在前面的基础上推出来的，即先验推导，怎么个先验法，其实就是二级频繁项集是在一级频繁项集的基础上产生的，三级频繁项集是在二级频繁项集的基础上产生的，以此类推。

　　Apriori算法属于候选消除算法，是一个生成候选集、消除不满足条件的候选集、并不断循环直到不再产生候选集的过程。

　　

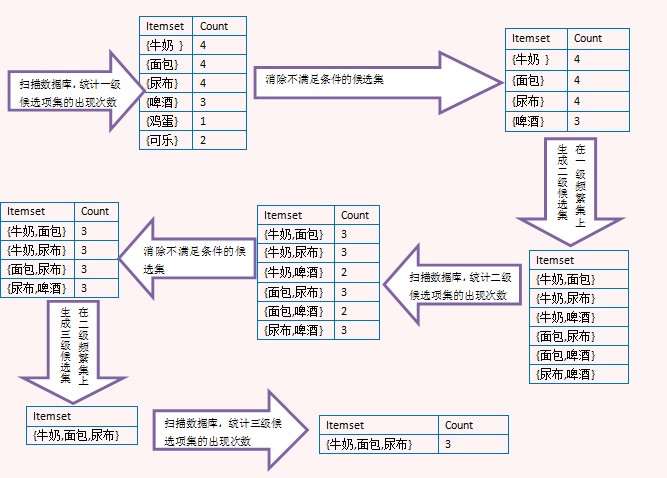
　　上面的图演示了Apriori算法的过程，注意看由二级频繁项集生成三级候选项集时，没有{牛奶,面包,啤酒}，那是因为{面包,啤酒}不是二级频繁项集，这里利用了Apriori定理。最后生成三级频繁项集后，没有更高一级的候选项集，因此整个算法结束，{牛奶,面包,尿布}是最大频繁子集。

　　算法的思想知道了，这里也就不上伪代码了，我认为理解了算法的思想后，子集去构思实现才能理解更深刻，这里贴一下我的关键代码：

 public static void main(String[] args) {
         // TODO Auto-generated method stub
         record = getRecord();// 获取原始数据记录
         List<List<String>> cItemset = findFirstCandidate();// 获取第一次的备选集
         List<List<String>> lItemset = getSupportedItemset(cItemset);// 获取备选集cItemset满足支持的集合

         while (endTag != true) {// 只要能继续挖掘
             List<List<String>> ckItemset = getNextCandidate(lItemset);// 获取第下一次的备选集
             List<List<String>> lkItemset = getSupportedItemset(ckItemset);// 获取备选集cItemset满足支持的集合
             getConfidencedItemset(lkItemset, lItemset, dkCountMap, dCountMap);// 获取备选集cItemset满足置信度的集合
             if (confItemset.size() != 0)// 满足置信度的集合不为空
                 printConfItemset(confItemset);// 打印满足置信度的集合
             confItemset.clear();// 清空置信度的集合
             cItemset = ckItemset;// 保存数据，为下次循环迭代准备
             lItemset = lkItemset;
             dCountMap.clear();
             dCountMap.putAll(dkCountMap);
         }

　　如果想看完整的代码，可以查看我的github，数据集的格式跟本文所述的略有不通，但不影响对算法的理解。

　　下一篇将介绍效率更高的算法--FP-Grow算法。

参考文档：http://www.cnblogs.com/fengfenggirl/p/associate_apriori.html