Python开发【数据结构】：算法（二）

堆排序

1、—树与二叉树简介

树是一种数据结构比如：目录结构

树是一种可以递归定义的数据结构

树是由n个节点组成的集合：

如果n=0，那这是一棵空树；
如果n>0，那存在1个节点作为树的根节点，其他节点可以分为m个集合，每个集合本身又是一棵树；

一些概念

根节点、
叶子节点
树的深度（高度）
树的度
孩子节点/父节点
子树

示图：

2、二叉树

二叉树：度不超过2的树（节点最多有两个叉）

示图：

3、两种特殊二叉树

满二叉树
完全二叉树

示图：

4、二叉树的存储方式

链式存储方式
顺序存储方式（列表）

示图：

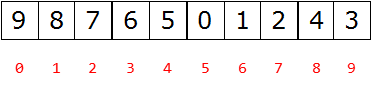
父节点和左孩子节点的编号下标有什么关系？

0-1 1-3 2-5 3-7 4-9
i ~ 2i+1

父节点和右孩子节点的编号下标有什么关系？

0-2 1-4 2-6 3-8 4-10
i – 2i+2

5、堆

堆：

大根堆：一棵完全二叉树，满足任一节点都比其孩子节点大
小根堆：一棵完全二叉树，满足任一节点都比其孩子节点小

大根堆：

小根堆：

6、堆排序过程

建立堆
得到堆顶元素，
为最大元素去掉堆顶，将堆最后一个元素放到堆顶，此时可通过一次调整重新使堆有序。
堆顶元素为第二大元素
重复步骤3，直到堆变空

7、构造堆

def sift(data,low,high):

    #low 要调整范围的根节点

    #high 整个data的最后一个节点

    i = low

    j = 2 * i  + 1  #左孩子

    tmp = data[i]  #去出跟节点

    while j <= high:   #左孩子在列表里面，表明i有孩子

        if j+1 <= high and data[j] < data[j+1]:      #如果有右孩子并且右孩子比左孩子大

            j = j + 1

        if data[j] > tmp:

            data[i] = data[j]

            i = j

            j = 2 *i +1

        else:

            break

    data[i] = tmp

def heap_sort(data):

    n = len(data)

    for i  in range(n//2-1,-1,-1):      # n//2-1 固定用法

        sift(data,i,n-1)                # 构造堆

8、堆排序

完整代码：

import time

import random

def call_time(func):

    def inner(*args,**kwargs):

        t1 = time.time()

        re = func(*args,**kwargs)

        t2 = time.time()

        print('Time cost:',func.__name__,t2-t1)

        return re

    return inner

def sift(data,low,high):

    #low 要调整范围的根节点

    #high 整个data的最后一个节点

    i = low

    j = 2 * i  + 1  #左孩子

    tmp = data[i]  #去出跟节点

    while j <= high:   #左孩子在列表里面，表明i有孩子

        if j+1 <= high and data[j] < data[j+1]:      #如果有右孩子并且右孩子比左孩子大

            j = j + 1

        if data[j] > tmp:

            data[i] = data[j]

            i = j

            j = 2 *i +1

        else:

            break

    data[i] = tmp

@call_time

def heap_sort(data):

    n = len(data)

    for i  in range(n//2-1,-1,-1):      # n//2-1 固定用法

        sift(data,i,n-1)                # 构造堆

    for i in range(n):              # 循环n次每次出一个数

        data[0],data[n-1-i] = data[n-1-i],data[0]

        sift(data,0,n-1-i-1)

data = list(range(10000))

random.shuffle(data)

heap_sort(data)

# Time cost: heap_sort 0.08801126480102539

时间复杂度：O(nlogn)

归并排序

将两段有序列表，将其合并为一个有序列表

例：

[2,5,7,8,91,3,4,6]

思路:

分解：将列表越分越小，直至分成一个元素

一个元素是有序的

合并：将两个有序列表归并，列表越来越大

代码：

import time

import random

def call_time(func):

    def inner(*args,**kwargs):

        t1 = time.time()

        re = func(*args,**kwargs)

        t2 = time.time()

        print('Time cost:',func.__name__,t2-t1)

        return re

    return inner

def merge(li, low, mid, high):

    i = low

    j = mid + 1

    ltmp = []

    while i <= mid and j <= high:

        if li[i] < li[j]:

            ltmp.append(li[i])

            i += 1

        else:

            ltmp.append(li[j])

            j += 1

    while i <= mid:

        ltmp.append(li[i])

        i += 1

    while j <= high:

        ltmp.append(li[j])

        j += 1

    li[low:high+1] = ltmp

def _mergesort(li, low, high):

    if low < high:

        mid = (low + high) // 2

        _mergesort(li,low, mid)

        _mergesort(li, mid+1, high)

        merge(li, low, mid, high)

@call_time

def mergesort(li):

    _mergesort(li, 0, len(li) - 1)

data = list(range(10000))

random.shuffle(data)

mergesort(data)

# Time cost: mergesort 0.0835103988647461

时间复杂度：O(nlogn)　　

希尔排序

希尔排序是一种分组插入排序算法。

首先取一个整数d1=n/2，将元素分为d1个组，每组相邻量元素之间距离为d1，在各组内进行直接插入排序；

取第二个整数d2=d1/2，重复上述分组排序过程，直到di=1，即所有元素在同一组内进行直接插入排序。

希尔排序每趟并不使某些元素有序，而是使整体数据越来越接近有序；最后一趟排序使得所有数据有序

代码：

import time

import random

def call_time(func):

    def inner(*args,**kwargs):

        t1 = time.time()

        re = func(*args,**kwargs)

        t2 = time.time()

        print('Time cost:',func.__name__,t2-t1)

        return re

    return inner

@call_time

def shell_sort(li):

    gap = len(li) // 2

    while gap >= 1:

        for i in range(gap, len(li)):

            tmp = li[i]

            j = i - gap

            while j >= 0 and tmp < li[j]:

                li[j + gap] = li[j]

                j -= gap

            li[j + gap] = tmp

        gap = gap // 2

data = list(range(10000))

random.shuffle(data)

shell_sort(data)

# Time cost: shell_sort 0.1275160312652588

时间复杂度：O(nlogn)

快速排序、堆排序、归并排序对比：

三种排序算法的时间复杂度都是O(nlogn)

一般情况下，就运行时间而言：

快速排序 < 归并排序 < 堆排序

三种排序算法的缺点：

快速排序：极端情况下排序效率低
归并排序：需要额外的内存开销
堆排序：在快的排序算法中相对较慢

比较时间：

quick_sort(data1)    # 快排

heap_sort(data2)     # 堆排

mergesort(data3)     # 归排

sys_sort(data4)        #系统自带

# Time cost: quick_sort 0.053006649017333984

# Time cost: heap_sort 0.08601117134094238

# Time cost: mergesort 0.08000993728637695

# Time cost: sys_sort 0.004500627517700195

视图：

第二十八章