[NOIP2008]双栈排序 【二分图 + 模拟】

题目描述

Tom最近在研究一个有趣的排序问题。如图所示，通过2个栈S1和S2，Tom希望借助以下4种操作实现将输入序列升序排序。

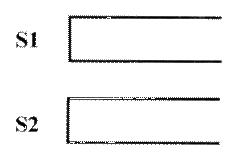
操作a

如果输入序列不为空，将第一个元素压入栈S1

操作b

如果栈S1不为空，将S1栈顶元素弹出至输出序列

操作c

如果输入序列不为空，将第一个元素压入栈S2

操作d

如果栈S2不为空，将S2栈顶元素弹出至输出序列

如果一个1~n的排列P可以通过一系列操作使得输出序列为1，2，…，(n-1)，n，Tom就称P是一个“可双栈排序排列”。例如(1,3,2,4)就是一个“可双栈排序序列”，而(2,3,4,1)不是。下图描述了一个将(1,3,2,4)排序的操作序列：<a,c,c,b,a,d,d,b>

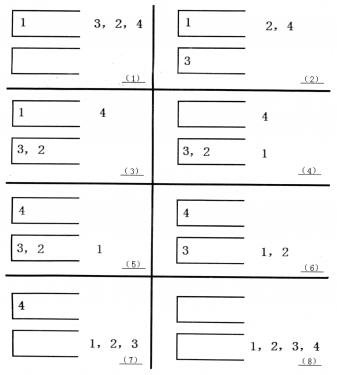
当然，这样的操作序列有可能有几个，对于上例(1,3,2,4)，<a,c,c,b,a,d,d,b>是另外一个可行的操作序列。Tom希望知道其中字典序最小的操作序列是什么。

输入输出格式

输入格式：

输入文件twostack.in的第一行是一个整数n。

第二行有n个用空格隔开的正整数，构成一个1~n的排列。

输出格式：

输出文件twostack.out共一行，如果输入的排列不是“可双栈排序排列”，输出数字0；否则输出字典序最小的操作序列，每两个操作之间用空格隔开，行尾没有空格。

输入输出样例

输入样例#1：

【输入样例1】
4
1 3 2 4
【输入样例2】
4
2 3 4 1
【输入样例3】
3
2 3 1

输出样例#1：

【输出样例1】
a b a a b b a b
【输出样例2】
0
【输出样例3】
a c a b b d

说明

30%的数据满足： n<=10

50%的数据满足： n<=50

100%的数据满足： n<=1000

题解

本蒟蒻刚开始就陷入了贪心的思维，结果30分。。WA

为什么会这样呢？按照贪心的思维，对于当前元素，优先考虑扔进s1，扔不进再考虑弹出s1，弹不出再考虑扔进s2，再考虑弹出s2，还弹不出就无解

看起来很完美= =，实际上暗藏漏洞——这个算法会将一些可行的情况判为无解

因为当你将一个元素扔进s1时，当前是最优了，但这个元素会对之后的元素产生影响，这个是没有考虑进去的，所以这个时候有可能扔进s2才可能有解

具体怎么做呢？

想想，对于扔进同一个栈的两个数A[i] < A[j] 且 i < j，，在j扔进去之前，i一定已经弹出来了，这个时候如果j后面如果还存在这比A[i]小的数，说明A[i]此时不应弹出来，这就形成矛盾了，所以这样的情况i与j不能同时存在于一个栈中

即对于所有i < j && A[i] < A[j],若存在k > j && A[k] < A[i]，则i和j不在同一栈中

由这个关系我们可以利用二分图求解：

对于所有不能存在与同一栈的元素之间连边，对二分图进行一次二分染色【优先染1号色，即入s1栈】，如果染色成功，则有解，且每个数改进哪一个栈也已经确定

最后就是模拟，题目说这是一个1~n的排列= =【一开始没看到弄了好久】，所以我们记录下当前应该弹出哪一个数，

对于进s1的数，能进则进，不能进就弹

对于进s2的数，进之前先看看s1能不能弹【即s1栈顶是不是当前该弹出的数】，再进行s2的操作：能进则进，否则就弹

最后就解出来啦~~

#include<iostream>
#include<cstdio>
#include<cstring>
#include<stack>
#include<algorithm>
#define LL long long int
using namespace std;
const int maxn = 1005,maxm = 100005,INF = 2000000000;

inline int read(){
	int out = 0,flag = 1;char c = getchar();
	while (c < 48 || c > 57) {if (c == '-') flag = -1;c = getchar();}
	while (c >= 48 &&c <= 57) {out = out * 10 + c - 48;c = getchar();}
	return out * flag;
}

int N,A[maxn],Min[maxn],color[maxn];

struct node{
	int v,id;
}e[maxn];

inline bool operator < (const node& a,const node& b){
	return a.v < b.v;
}

int head[maxn],nedge = 0;
struct EDGE{
	int to,next;
}edge[maxm];

inline void build(int u,int v){
	edge[nedge] = (EDGE) {v,head[u]};
	head[u] = nedge++;
	edge[nedge] = (EDGE) {u,head[v]};
	head[v] = nedge++;
}

void init(){
	fill(head,head + maxn,-1);
	N = read();
	for (int i = 1; i <= N; i++){
		e[i].v = A[i] = read();
		e[i].id = i;
	}
	Min[N + 1] = INF;
	for (int i = N; i > 0; i--) Min[i] = min(A[i],Min[i + 1]);
}

bool flag = true;

void dfs(int u,int c){
	color[u] = c;
	int to;
	for (int k = head[u]; k != -1; k = edge[k].next)
		if (!color[to = edge[k].to]){
			dfs(to,((c - 1) ^ 1) + 1);
			if (!flag) return;
		}else if (color[to] == color[u]){
			flag = false;
			return;
		}
}

void Build(){
	for (int i = 1; i <= N; i++)
		for (int j = i + 1; j <= N; j++)
			if (A[i] < A[j] && A[i] > Min[j + 1])
				build(i,j);
	for (int i = 1; i <= N; i++){
		if (!color[i]){
			dfs(i,1);
			if (!flag) return;
		}
	}
}

const char *alpha = "abcd";
int ans[2 * maxn],ansi = 0;
stack<int> s[2];

void solve(){
	int cnt = 1;
	for (int i = 1; i <= N; i++){
		if (color[i] == 1){
			s[0].push(A[i]);
			ans[++ansi] = 0;
		}else {
			s[1].push(A[i]);
			ans[++ansi] = 2;
		}
		while (!s[0].empty() && s[0].top() == cnt){
			s[0].pop();
			ans[++ansi] = 1;
			cnt++;
		}
		while (!s[1].empty() && s[1].top() == cnt){
			s[1].pop();
			ans[++ansi] = 3;
			cnt++;
		}
	}
	while (!s[0].empty() || !s[1].empty()){
		if (!s[0].empty() && s[0].top() == cnt){
			s[0].pop();
			ans[++ansi] = 1;
			cnt++;
		}
		if (!s[1].empty() && s[1].top() == cnt){
			s[1].pop();
			ans[++ansi] = 3;
			cnt++;
		}
	}
}

int main(){
	init();
	Build();
	if (!flag) cout<<0<<endl;
	else {
		/*for (int i = 1; i <= N; i++) printf("%d ",color[i]);
		cout<<endl;*/
		solve();
		printf("%c",alpha[ans[1]]);
		for (int i = 2; i <= ansi; i++)
			printf(" %c",alpha[ans[i]]);
		printf("\n");
	}
	return 0;
}