模反元素 RSA Euler's totient function

https://baike.baidu.com/item/模反元素/20417595

如果两个正整数a和n互质，那么一定可以找到整数b，使得 ab-1 被n整除，或者说ab被n除的余数是1。这时，b就叫做a的“模反元素”

中文名 模反元素 外文名modulo multiplicative inverse 同义词 模逆元素

如果两个正整数a和n互质，那么一定可以找到整数b，使得 ab-1 被n整除，或者说ab被n除的余数是1。

这时，b就叫做a对模数n的“模反元素”。比如，3和11互质，那么3的模反元素就是4，因为 (3 × 4)-1 可以被11整除。显然，模反元素不止一个， 4加减11的整数倍都是3的模反元素 {…,-18,-7,4,15,26,…}，即如果b是a的模反元素，则 b+kn 都是a的模反元素。

欧拉定理可以用来证明模反元素必然存在。

可以看到，a的 φ(n)-1 次方，就是a对模数n的模反元素。

 

 RSA (cryptosystem) - Wikipedia https://en.wikipedia.org/wiki/RSA_(cryptosystem)

 

算法4步骤

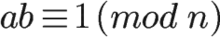
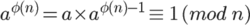
The RSA algorithm involves four steps: key generation, key distribution, encryption and decryption.

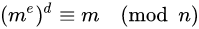
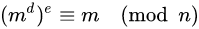
Euler's totient function - Wikipedia https://en.wikipedia.org/wiki/Euler%27s_totient_function

 

The first thousand values of φ(n). The points on the top line represent φ(p) when p is a prime number, which is p − 1.^[1]

In number theory, Euler's totient function counts the positive integers up to a given integer n that are relatively prime to n. It is written using the Greek letter phi as φ(n) or ϕ(n), and may also be called Euler's phi function. It can be defined more formally as the number of integers k in the range 1 ≤ k ≤ n for which the greatest common divisor gcd(n, k) is equal to 1.^[2][3] The integers k of this form are sometimes referred to as totatives of n.

For example, the totatives of n = 9 are the six numbers 1, 2, 4, 5, 7 and 8. They are all relatively prime to 9, but the other three numbers in this range, 3, 6, and 9 are not, because gcd(9, 3) = gcd(9, 6) = 3 and gcd(9, 9) = 9. Therefore, φ(9) = 6. As another example, φ(1) = 1 since for n = 1 the only integer in the range from 1 to n is 1 itself, and gcd(1, 1) = 1.

Euler's totient function is a multiplicative function, meaning that if two numbers m and n are relatively prime, then φ(mn) = φ(m)φ(n).^[4][5] This function gives the order of the multiplicative group of integers modulo n (the group of units of the ring ℤ/nℤ).^[6] It also plays a key role in the definition of the RSA encryption system.

1>
phi函数
phi(N)为小于正整数N的与N互质的正整数的个数
phi(10)=4
2>
欧拉定理
m(a^phi(n),n)=1
3>
应用
m(7^phi(10),10)=1
==>m(7^4,10)=1
7^222=(7^4)^55*7^2
==>m(7^222,10)=m(1^55,10)*m(7^2,10)=9

Carmichael number - Wikipedia https://en.wikipedia.org/wiki/Carmichael_number

In number theory, a Carmichael number is a composite number   which satisfies the modular arithmetic congruence relation:

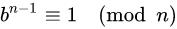
561=3*11*17
m(561-1,3-1)=m(561-1,11-1)=m(561-1,17-1)
1105=5*13*17
m(1105-1,5-1)=m(1105-1,13-1)=m(1105-1,17-1)

In number theory, the Carmichael function associates to every positive integer n a positive integer , defined as the smallest positive integer m such that

  for every integer a between 1 and n that is coprime to n.

https://baike.baidu.com/item/欧拉函数/1944850?fr=aladdin

欧拉函数

在数论，对正整数n，欧拉函数是小于n的正整数中与n互质的数的数目（φ(1)=1）。此函数以其首名研究者欧拉命名(Euler's totient function)，它又称为Euler's totient function、φ函数、欧拉商数等。 例如φ(8)=4，因为1,3,5,7均和8互质。 从欧拉函数引伸出来在环论方面的事实和拉格朗日定理构成了欧拉定理的证明。