堆排序原理及其js实现

图文来源：https://www.cnblogs.com/chengxiao/p/6129630.html

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。首先简单了解下堆结构。堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。首先简单了解下堆结构。

堆

　　堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。如下图：

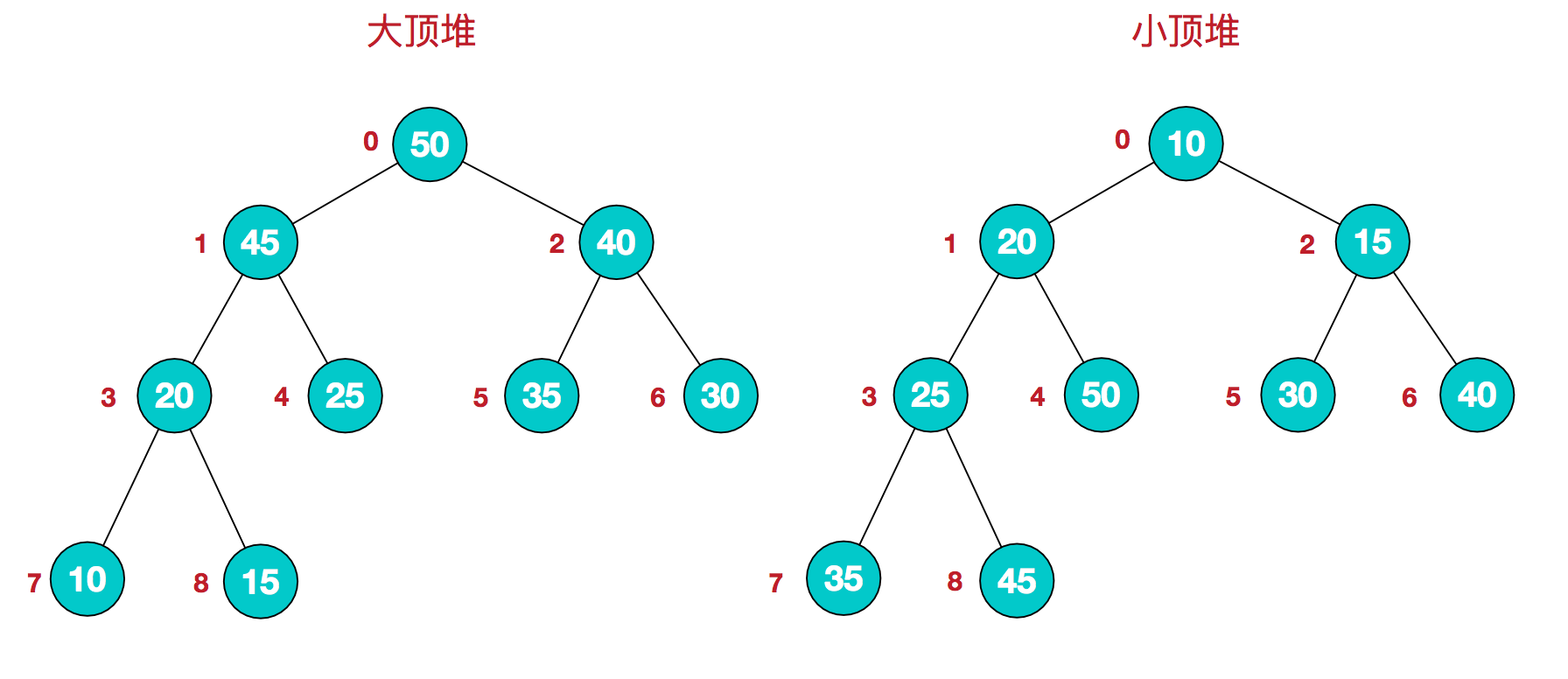
同时，我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子

该数组从逻辑上讲就是一个堆结构，我们用简单的公式来描述一下堆的定义就是：

大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]  

小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]  

接下来，我们来看看堆排序的基本思想及基本步骤：

堆排序基本思想及步骤

堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了

步骤一 构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。

　　a.假设给定无序序列结构如下

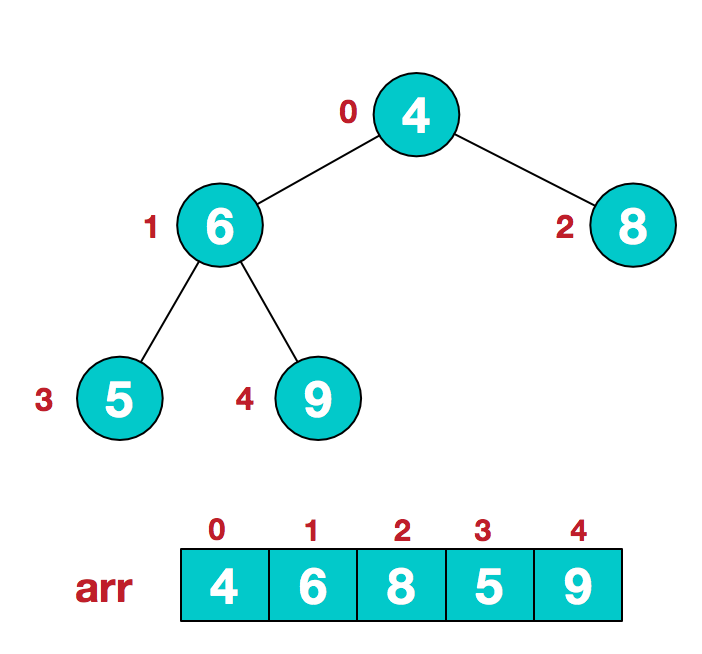
2.此时我们从最后一个非叶子结点开始（叶结点自然不用调整，第一个非叶子结点 arr.length/2-1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整。

3.

找到第二个非叶节点4，由于[4,9,8]中9元素最大，4和9交换。

这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。

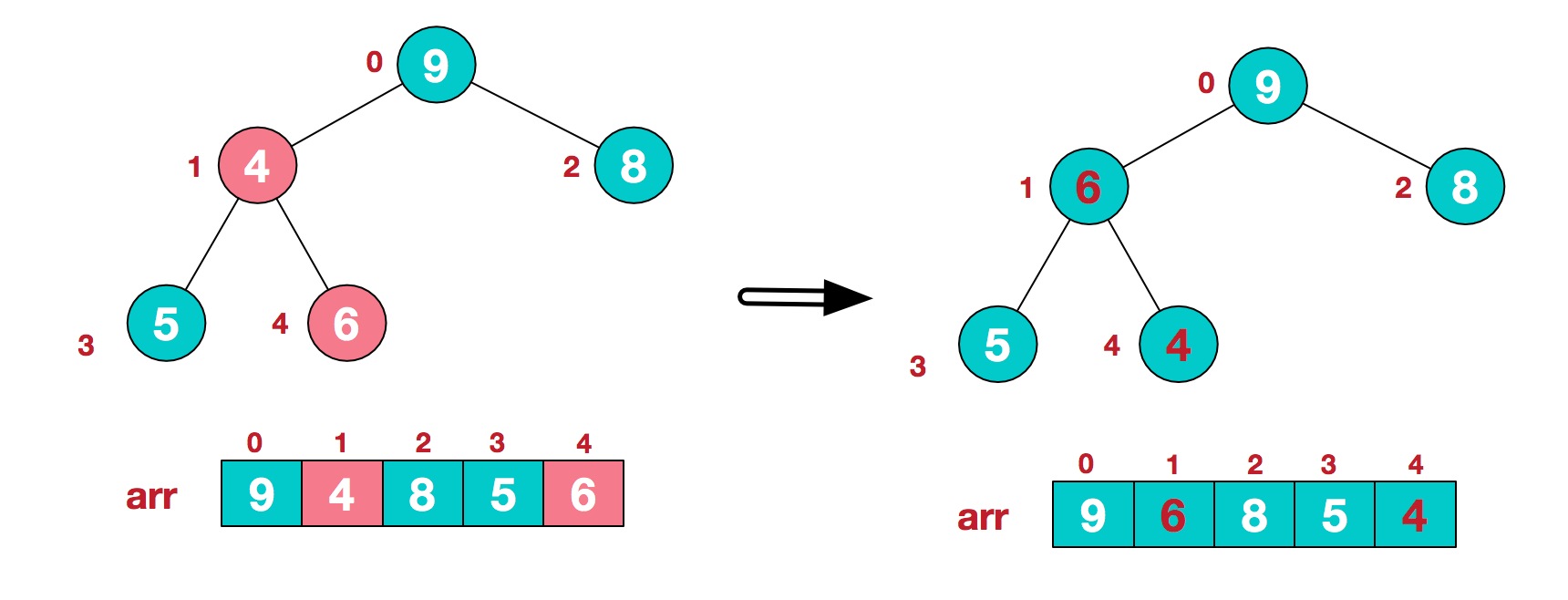
此时，我们就将一个无需序列构造成了一个大顶堆。

步骤二 将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。

a.将堆顶元素9和末尾元素4进行交换

b.重新调整结构，使其继续满足堆定义

c.再将堆顶元素8与末尾元素5进行交换，得到第二大元素8.

后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序

再简单总结下堆排序的基本思路：

　　a.将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;

　　b.将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;

　　c.重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

算法稳定性

堆排序是一种不稳定的排序方法。

因为在堆的调整过程中，关键字进行比较和交换所走的是该结点到叶子结点的一条路径，

因此对于相同的关键字就可能出现排在后面的关键字被交换到前面来的情况。

js代码实现堆排序

let dat=[1,5, 8, 10, 3, 2, 18, 17, 9];
        //生成大顶堆
        function adjustHeap(arr,i,len){
            //将当前值保存
            var temp=arr[i];
            //从i结点的左子结点开始，也就是2i+1处开始
            for(var j=2*i+1;j<len;j=2*j+1){
            //如果左子结点小于右子结点，j指向右子结点
            if((j+1<len)&&arr[j]<arr[j+1]){
                j++;
            }
                //如果子节点大于父节点，将子节点值赋给父节点（不用进行交换）值和索引都赋值
                if(arr[j]>temp){
                    arr[i]=arr[j];
                    i=j;
                }else{
                    break;
                }
            }
            arr[i]=temp;      //将temp值放到最终的位置

        }
        function heapSort(data) {
        //构造大顶堆
        //此时我们从最后一个非叶子结点开始,叶结点自然不用调整
        ////从第一个非叶子结点从下至上，从右至左调整结构
        for(var i=Math.floor(data.length/2-1);i>=0;i--){
            adjustHeap(data,i,data.length);
        }
      // console.log(data);
      //交换堆顶元素与末尾元素；不算最后一个元素，重新调整堆
      for(var k=data.length-1;k>0;k--){
        //将堆顶元素与末尾元素进行交换
        [data[0],data[k]]=[data[k],data[0]];
         // console.log(data);
         //不算最后一个元素，重新对堆进行调整
         adjustHeap(data,0,k);
//此处不用向上面调整一样for循环，因为此处只需要调整顶点，其他点已在上一步调整好，从顶点再往下调整，
     }
     return data;
}
var sortedData=heapSort(dat);
console.log(sortedData);