题解报告：poj 1113 Wall（凸包）

Description

Once upon a time there was a greedy King who ordered his chief Architect to build a wall around the King's castle. The King was so greedy, that he would not listen to his Architect's proposals to build a beautiful brick wall with a perfect shape and nice tall towers. Instead, he ordered to build the wall around the whole castle using the least amount of stone and labor, but demanded that the wall should not come closer to the castle than a certain distance. If the King finds that the Architect has used more resources to build the wall than it was absolutely necessary to satisfy those requirements, then the Architect will loose his head. Moreover, he demanded Architect to introduce at once a plan of the wall listing the exact amount of resources that are needed to build the wall.

Your task is to help poor Architect to save his head, by writing a program that will find the minimum possible length of the wall that he could build around the castle to satisfy King's requirements.
The task is somewhat simplified by the fact, that the King's castle has a polygonal shape and is situated on a flat ground. The Architect has already established a Cartesian coordinate system and has precisely measured the coordinates of all castle's vertices in feet.

Input

The first line of the input file contains two integer numbers N and L separated by a space. N (3 <= N <= 1000) is the number of vertices in the King's castle, and L (1 <= L <= 1000) is the minimal number of feet that King allows for the wall to come close to the castle.
Next N lines describe coordinates of castle's vertices in a clockwise order. Each line contains two integer numbers Xi and Yi separated by a space (-10000 <= Xi, Yi <= 10000) that represent the coordinates of ith vertex. All vertices are different and the sides of the castle do not intersect anywhere except for vertices.

Output

Write to the output file the single number that represents the minimal possible length of the wall in feet that could be built around the castle to satisfy King's requirements. You must present the integer number of feet to the King, because the floating numbers are not invented yet. However, you must round the result in such a way, that it is accurate to 8 inches (1 foot is equal to 12 inches), since the King will not tolerate larger error in the estimates.

Sample Input

Sample Output

Hint

结果四舍五入就可以了

解题思路：题意其实就是在一个凸包外建立一座围墙，要求围墙到凸包(城堡)的最小距离为L，求此围墙的最小总长度。公式：围墙的最小总长度=凸包周长+一个以L为半径的圆周长。证明：假设顺时针给出4个点A、B、C、D（都是凸包的顶点）组成一个凸四边形ABCD。不妨过A点作AE、AF分别垂直于AB、AD，过B点作BG、BH分别垂直于AB、BC......过A点以L为半径作一段弧连到AF，同理使GH成为一段弧。显然EG平行且等于AB......对其他顶点进行同样的操作后，可得出围墙的最小值=四边形的周长+四个顶点对应的弧长（半径都为L）之和。如图所示：

推广到任意凸多边形，每段圆弧都是以凸包上每个对应的顶点为圆心，给定的L为半径，与相邻两条边的切线之间的一段圆弧。每段圆弧的两条半径的夹角与凸包内对应的内角互补。设凸包上有n个顶点,则组成了n个圆周角，总角度数为360°*n=2*180°*n，凸包(凸多边形)的内角和为180°*(n-2)，作了2*n条垂线，那么所有垂角之和为2*n*90°=180°*n，因此所有小圆弧对应的圆心角之和为2*180°*n-180°*(n-2)-180°*n=360°（为一个以L为半径的圆）。综上所述，围墙的最小总长度=凸包周长+一个以L为半径的圆周长。

AC代码(63ms)：Graham-scan算法：时间复杂度为0(nlogn)。

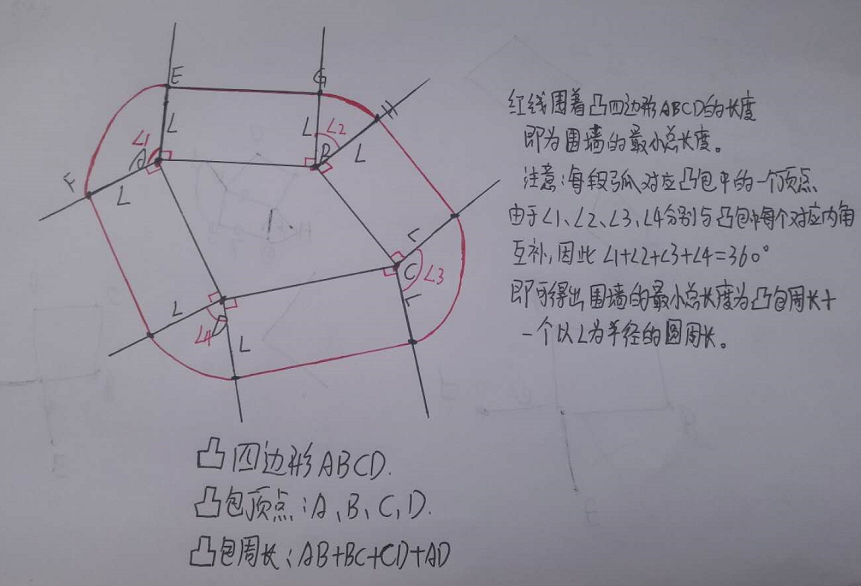
 #include<iostream>

 #include<string.h>

 #include<algorithm>

 #include<cstdio>

 #include<cmath>

 using namespace std;

 const int maxn=;

 const double PI=acos(-1.0);

 struct node{int x,y;};

 node vex[maxn];

 node stackk[maxn];

 bool cmp1(node a,node b){

     if(a.y==b.y)return a.x<b.x;

     else return a.y<b.y;

 }

 bool cmp2(node a,node b){

     double A=atan2(a.y-stackk[].y,a.x-stackk[].x);

     double B=atan2(b.y-stackk[].y,b.x-stackk[].x);

     if(A!=B)return A<B;

     else return a.x<b.x;

 }

 int cross(node p0,node p1,node p2){

     return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);

 }

 double dis(node a,node b){

     return sqrt((a.x-b.x)*(a.x-b.x)*1.0+(a.y-b.y)*(a.y-b.y));

 }

 int main(){

     int n,l;

     while(~scanf("%d%d",&n,&l)){

         for(int i=;i<n;++i)//输入t个点

             scanf("%d%d",&vex[i].x,&vex[i].y);

         memset(stackk,,sizeof(stackk));

         sort(vex,vex+n,cmp1);

         stackk[]=vex[];

         sort(vex+,vex+n,cmp2);

         stackk[]=vex[];

         int top=;

         for(int i=;i<n;++i){

             while(top>&&cross(stackk[top-],stackk[top],vex[i])<=)top--;

             stackk[++top]=vex[i];

         }

         double s=;

         for(int i=;i<=top;++i)

             s+=dis(stackk[i-],stackk[i]);

         s+=dis(stackk[top],vex[]);

         s+=*PI*l;//加上圆的周长

         printf("%d\n",(int)(s+0.5));//四舍五入

     }

     return ;

 }

AC代码二(32ms)：Andrew算法：时间复杂度为O(nlogn)，但比Graham-scan算法还快！

 #include<iostream>

 #include<string.h>

 #include<algorithm>

 #include<cstdio>

 #include<cmath>

 using namespace std;

 const int maxn=;

 const double PI=acos(-1.0);

 struct node{int x,y;}vex[maxn],stackk[maxn];

 bool cmp(node a,node b){//坐标排序

     return ((a.y<b.y)||(a.y==b.y&&a.x<b.x));

 }

 int cross(node p0,node p1,node p2){

     return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);

 }

 double dis(node a,node b){

     return sqrt((a.x-b.x)*(a.x-b.x)*1.0+(a.y-b.y)*(a.y-b.y));

 }

 int main(){

     int n,l;

     while(~scanf("%d%d",&n,&l)){

         for(int i=;i<n;++i)

             scanf("%d%d",&vex[i].x,&vex[i].y);

         memset(stackk,,sizeof(stackk));

         sort(vex,vex+n,cmp);

         int top=-;

         for(int i=;i<n;++i){//构造凸包下侧

             while(top>&&cross(stackk[top-],stackk[top],vex[i])<=)top--;

             stackk[++top]=vex[i];

         }

         for(int i=n-,k=top;i>=;--i){//构造凸包上侧

             while(top>k&&cross(stackk[top-],stackk[top],vex[i])<=)top--;

             stackk[++top]=vex[i];

         }

         double s=;

         for(int i=;i<=top;++i)//计算凸包周长

             s+=dis(stackk[i-],stackk[i]);

         s+=*PI*l;

         printf("%d\n",(int)(s+0.5));

     }

     return ;

 }