Leetcode 335.路径交叉

路径交叉

给定一个含有 n 个正数的数组 x。从点 (0,0) 开始，先向北移动 x[0] 米，然后向西移动 x[1] 米，向南移动 x[2] 米，向东移动 x[3] 米，持续移动。也就是说，每次移动后你的方位会发生逆时针变化。

编写一个 O(1) 空间复杂度的一趟扫描算法，判断你所经过的路径是否相交。

示例 1:

输入: [2,1,1,2]

输出: true

解释: 路径交叉了

示例 2:

输入: [1,2,3,4]

输出: false

解释: 路径没有相交

示例 3:

输入: [1,1,1,1]

输出: true

解释: 路径相交了

相交的情况只有以下三种情况：

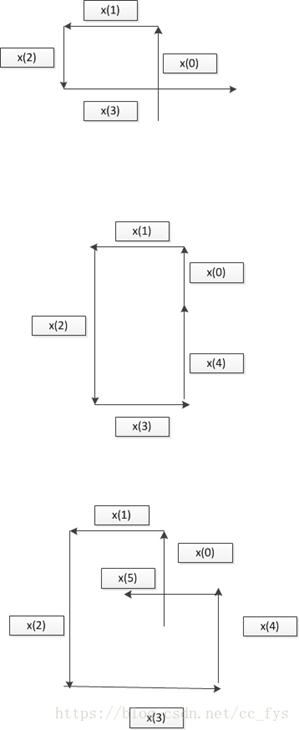
情况1：

X(3)和x(0)相交，需满足条件x(2)<=x(0)且x(3)>=x(1)

情况2：

X(4)和x(0)相交，需满足条件x(1)=x(3)且x(4)+x(0)>=x(2)

情况3：

X(5)和x(0)相交，需满足条件x(2)>x(0)且x(3)>x(1)且x(4)<x(2)且x(3)>x(1)且x(5)+x(1)>=x(3)且x(4)+x(0)>=x(2)

 class Solution {
     public boolean isSelfCrossing(int[] x) {
         for(int i=3;i<x.length;i++){
             if(x[i]>=x[i-2]&&x[i-3]>=x[i-1]){
                 return true;
             }
             if(i>=4&&x[i-1]==x[i-3]&&x[i]>=x[i-2]-x[i-4]){
                 return true;
             }
             if(i>=5&&x[i-2]>=x[i-4]&&x[i-3]>=x[i-1]&&x[i-1]>=x[i-3]-x[i-5]&&x[i]>=x[i-2]-x[i-4]){
                 return true;
             }
         }
         return false;
     }
 }