Go -- LRU算法(缓存淘汰算法)(转)

1. LRU
1.1. 原理

LRU（Least recently used，最近最少使用）算法根据数据的历史访问记录来进行淘汰数据，其核心思想是“如果数据最近被访问过，那么将来被访问的几率也更高”。

1.2. 实现

最常见的实现是使用一个链表保存缓存数据，详细算法实现如下：

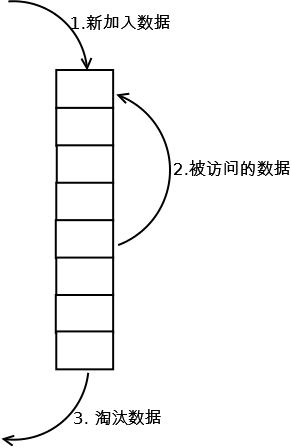
1. 新数据插入到链表头部；

2. 每当缓存命中（即缓存数据被访问），则将数据移到链表头部；

3. 当链表满的时候，将链表尾部的数据丢弃。

1.3. 分析

【命中率】

当存在热点数据时，LRU的效率很好，但偶发性的、周期性的批量操作会导致LRU命中率急剧下降，缓存污染情况比较严重。

【复杂度】

实现简单。

【代价】

命中时需要遍历链表，找到命中的数据块索引，然后需要将数据移到头部。

2. LRU-K（描述有误，请勿参考）

2.1. 原理

LRU-K中的K代表最近使用的次数，因此LRU可以认为是LRU-1。LRU-K的主要目的是为了解决LRU算法“缓存污染”的问题，其核心思想是将“最近使用过1次”的判断标准扩展为“最近使用过K次”。

2.2. 实现

相比LRU，LRU-K需要多维护一个队列，用于记录所有缓存数据被访问的历史。只有当数据的访问次数达到K次的时候，才将数据放入缓存。当需要淘汰数据时，LRU-K会淘汰第K次访问时间距当前时间最大的数据。详细实现如下：

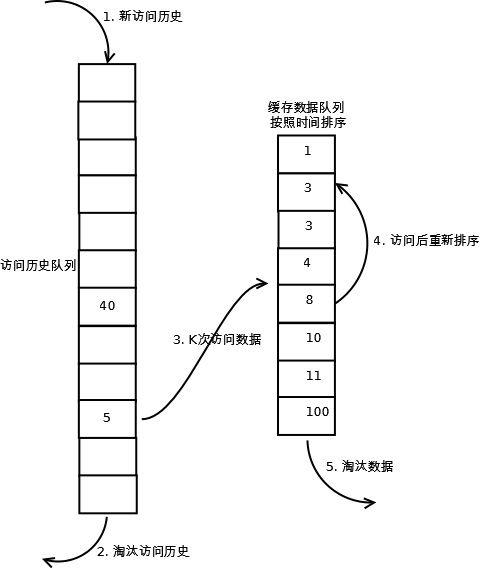
1. 数据第一次被访问，加入到访问历史列表；

2. 如果数据在访问历史列表里后没有达到K次访问，则按照一定规则（FIFO，LRU）淘汰；

3. 当访问历史队列中的数据访问次数达到K次后，将数据索引从历史队列删除，将数据移到缓存队列中，并缓存此数据，缓存队列重新按照时间排序；

4. 缓存数据队列中被再次访问后，重新排序；

5. 需要淘汰数据时，淘汰缓存队列中排在末尾的数据，即：淘汰“倒数第K次访问离现在最久”的数据。

LRU-K具有LRU的优点，同时能够避免LRU的缺点，实际应用中LRU-2是综合各种因素后最优的选择，LRU-3或者更大的K值命中率会高，但适应性差，需要大量的数据访问才能将历史访问记录清除掉。

2.3. 分析

【命中率】

LRU-K降低了“缓存污染”带来的问题，命中率比LRU要高。

【复杂度】

LRU-K队列是一个优先级队列，算法复杂度和代价比较高。

【代价】

由于LRU-K还需要记录那些被访问过、但还没有放入缓存的对象，因此内存消耗会比LRU要多；当数据量很大的时候，内存消耗会比较可观。

LRU-K需要基于时间进行排序（可以需要淘汰时再排序，也可以即时排序），CPU消耗比LRU要高。

3. Two queues（2Q）

3.1. 原理

Two queues（以下使用2Q代替）算法类似于LRU-2，不同点在于2Q将LRU-2算法中的访问历史队列（注意这不是缓存数据的）改为一个FIFO缓存队列，即：2Q算法有两个缓存队列，一个是FIFO队列，一个是LRU队列。

3.2. 实现

当数据第一次访问时，2Q算法将数据缓存在FIFO队列里面，当数据第二次被访问时，则将数据从FIFO队列移到LRU队列里面，两个队列各自按照自己的方法淘汰数据。详细实现如下：

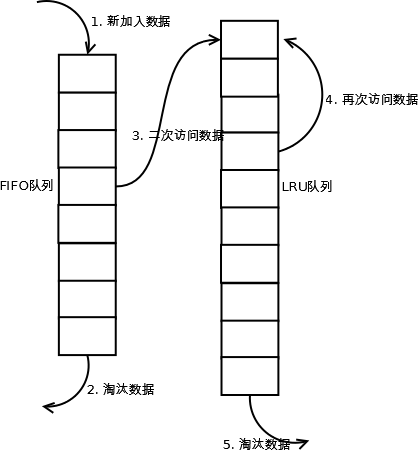
1. 新访问的数据插入到FIFO队列；

2. 如果数据在FIFO队列中一直没有被再次访问，则最终按照FIFO规则淘汰；

3. 如果数据在FIFO队列中被再次访问，则将数据移到LRU队列头部；

4. 如果数据在LRU队列再次被访问，则将数据移到LRU队列头部；

5. LRU队列淘汰末尾的数据。

注：上图中FIFO队列比LRU队列短，但并不代表这是算法要求，实际应用中两者比例没有硬性规定。

3.3. 分析

【命中率】

2Q算法的命中率要高于LRU。

【复杂度】

需要两个队列，但两个队列本身都比较简单。

【代价】

FIFO和LRU的代价之和。

2Q算法和LRU-2算法命中率类似，内存消耗也比较接近，但对于最后缓存的数据来说，2Q会减少一次从原始存储读取数据或者计算数据的操作。

4. Multi Queue（MQ）

4.1. 原理

MQ算法根据访问频率将数据划分为多个队列，不同的队列具有不同的访问优先级，其核心思想是：优先缓存访问次数多的数据。

4.2. 实现

MQ算法将缓存划分为多个LRU队列，每个队列对应不同的访问优先级。访问优先级是根据访问次数计算出来的，例如

详细的算法结构图如下，Q0，Q1....Qk代表不同的优先级队列，Q-history代表从缓存中淘汰数据，但记录了数据的索引和引用次数的队列：

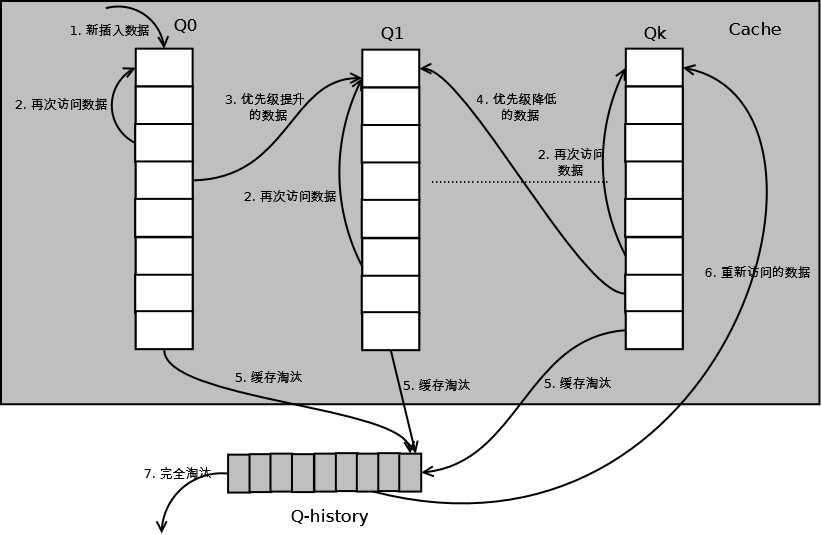
如上图，算法详细描述如下：

1. 新插入的数据放入Q0；

2. 每个队列按照LRU管理数据；

3. 当数据的访问次数达到一定次数，需要提升优先级时，将数据从当前队列删除，加入到高一级队列的头部；

4. 为了防止高优先级数据永远不被淘汰，当数据在指定的时间里访问没有被访问时，需要降低优先级，将数据从当前队列删除，加入到低一级的队列头部；

5. 需要淘汰数据时，从最低一级队列开始按照LRU淘汰；每个队列淘汰数据时，将数据从缓存中删除，将数据索引加入Q-history头部；

6. 如果数据在Q-history中被重新访问，则重新计算其优先级，移到目标队列的头部；

7. Q-history按照LRU淘汰数据的索引。

4.3. 分析

【命中率】

MQ降低了“缓存污染”带来的问题，命中率比LRU要高。

【复杂度】

MQ需要维护多个队列，且需要维护每个数据的访问时间，复杂度比LRU高。

【代价】

MQ需要记录每个数据的访问时间，需要定时扫描所有队列，代价比LRU要高。

注：虽然MQ的队列看起来数量比较多，但由于所有队列之和受限于缓存容量的大小，因此这里多个队列长度之和和一个LRU队列是一样的，因此队列扫描性能也相近。

5. LRU类算法对比

由于不同的访问模型导致命中率变化较大，此处对比仅基于理论定性分析，不做定量分析。

对比点	对比
命中率	LRU-2 > MQ(2) > 2Q > LRU
复杂度	LRU-2 > MQ(2) > 2Q > LRU
代价	LRU-2  > MQ(2) > 2Q > LRU

实际应用中需要根据业务的需求和对数据的访问情况进行选择，并不是命中率越高越好。例如：虽然LRU看起来命中率会低一些，且存在”缓存污染“的问题，但由于其简单和代价小，实际应用中反而应用更多。