Codeforces Round #626 (Div. 2)

Contest Info

Solved	A	B	C	D	E	F
4/6	O	Ø	Ø	Ø	Ø	-

O 在比赛中通过
Ø 赛后通过
! 尝试了但是失败了
- 没有尝试

Solutions

B.Count Subrectangles

题意：

给出$a$和$b$两个数列，构造一个矩阵$c$，使得$c_{i,j}=a_i∗b_j$，求矩阵$c$中有多少个面积为$k$的小矩阵里的值全为$1$

思路：

我们对面积为$k$的矩形边长进行枚举，即遍历$k$的所有因子（只用枚举到$sqrt(k)$，否则会超时）

表示在$a$数组有$ i $个连续的$1$，那么如果在$b$数组里有$ k/i $个连续的$1$，形成的矩形面积就是$k$。计算出$a$数组中符合条件的个数乘以$b$数组中符合条件的个数，然后把每个因子下的都加起来就是答案

根据矩阵$c$的构造原理可知，每一行相邻元素的连续性由$b$决定，每一列的连续性由$a$决定，因此我们可以先做下预处理

#include <cstdio>

#include <cstring>

#include <algorithm>

#include <cmath>

#define ll long long

using namespace std;

const int maxn = 4e4+100;

int n, m, k;

ll ans, cnta[maxn], cntb[maxn];

void cal(int num, ll *cnt){

    int tmp, now = 0;

    for(int i = 1; i <= num; i++){

        scanf("%d", &tmp);

        if(tmp==1) now++;

        else{

            for(int j = 1; j <= now; j++) cnt[j] += now-j+1;

            now = 0;

        }

    }

    for(int j = 1; j <= now; j++) cnt[j] += now-j+1;

}

int main(){

    scanf("%d%d%d", &n, &m, &k);

    cal(n, cnta), cal(m, cntb);

    for(int i = 1; i <= sqrt(k); i++){

        if(k%i!=0) continue;

        if(i<=n&&k/i<=m) ans += cnta[i]*cntb[k/i];

        if(i!=k/i&&i<=m&&k/i<=n) ans += cntb[i]*cnta[k/i];

    }

    printf("%lld", ans);

}

C.Unusual Competitions

题意：

给定一个括号序列，每次可以选择一个区间$[l,r]$来重排，耗时$r−l+1$，求最少需要多少时间使其变得正常（左右括号完全匹配）

思路：

假如我们把$($看作$1$，$)$看作$-1$，那么对于一段长度为$n$的合法的括号序列，对于$[1,i](i\in [1,n))$的前缀和一定是大与$0$的

那么什么时候重排呢？

一段不合法的括号序列左括号的数量等于右括号时

比赛的时候我是只想到左括号数量等于右括号的时候重排，但是对于不合法的状态没有进行有效的判断，其实就是出现前缀和小于0的情况就可以认为当前这段左右括号相等的序号是不合法的

#include <cstdio>

#include <cstring>

#include <algorithm>

using namespace std;

const int maxn = 1e6+100;

int n, top, ans, cnt[1010];

char a[maxn], sta[maxn];

int main(){

    scanf("%d%s", &n, a+1);

    if(n%2==1) return !printf("-1");

    for(int i = 1; i <= n; i++){

        if(sta[top]=='('&&a[i]==')') top--, cnt['(']--;

        else {

            sta[++top] = a[i], cnt[a[i]]++;

        }

        if(cnt['(']==cnt[')']&&top==cnt['(']+cnt[')']){

            ans += top;

            top = cnt['('] = cnt[')'] = 0;

        }

    }

    if(top==0) printf("%d", ans);

    else printf("-1");

}

(WA)

#include <cstdio>

#include <cstring>

#include <algorithm>

using namespace std;

const int maxn = 1e6+100;

int n, ans, last, sum;

char a[maxn];

int main(){

    scanf("%d%s", &n, a+1);

    for(int i = 1; i <= n; i++){

        int tmp = sum;

        a[i]=='(' ? sum++ : sum--;

        if(sum==0&&tmp>0) last = i;

        else if(sum==0&&tmp<0) ans += i-last, last = i;

    }

    if(last==n) printf("%d", ans);

    else printf("-1");

}

/*

8

)))()(((

*/

//Despired by LoveXJH

(AC)

D.Present

题意：

给定大小为$n$的$a$数组，求下面式子的结果：

　　　　　　　　　　　　　　　　$$(a_1 + a_2) \oplus (a_1 + a_3) \oplus \ldots \oplus (a_1 + a_n) \\ \oplus (a_2 + a_3) \oplus \ldots \oplus (a_2 + a_n) \\ \ldots \\ \oplus (a_{n-1} + a_n) \\$$

思路：

有关位运算的题目我们可以考虑按位处理

因为两个元素的和$<=2e7$，而$2e7$小于$2^{25}$，因此结果最多是$25$位。我们考虑答案中每一位$ans[k]$的值$(0\leq k\leq 24)$

显然，$a_i$中仅有$0～k$位会对第$k$位有影响，因此对数组$a$全部对$2^(k+1)$取模，得到数组$b$，对$b$按升序排序。

这样，$0\leq b_i\leq 2^{k+1}-1$，两个$b_i$的和$\leq 2^{k+2}-2$。要使得和的第$k$位为$1$，和的范围应该为$[ 2^k , 2^{k+1}-1 ] $（区间1）或者$ [ 2^k+2^{k+1} , 2^{k+2}-2] $（区间2）。

枚举$b_i$，对两个区间可分别得到另一个和$b_i$相加的元素$b_j$的范围大小，利用二分查找$b_j$的区间，从而得到$b_j$的个数$num$。枚举完之后$num\%2=1$的话，答案中的第$k$位便是$1$。

#include <cstdio>

#include <cstring>

#include <algorithm>

using namespace std;

const int maxn = 4e5+100;

int n, ans;

int a[maxn], b[maxn], p[26];

int cal(int k){

    for(int i = 1; i <= n; i++) b[i] = a[i]%(1<<(k+1));

    sort(b+1, b+1+n);

    int res = 0;

    for(int i = 1; i <= n; i++){

        int x = b[i];

        res += upper_bound(b+i+1, b+1+n, p[k+1]-1-x)-lower_bound(b+i+1, b+1+n, p[k]-x);

        res += upper_bound(b+i+1, b+1+n, p[k+2]-2-x)-lower_bound(b+i+1, b+1+n, p[k+1]+p[k]-x);

    }

    return res%2;

}

int main(){

    scanf("%d", &n);

    for(int i = 1; i <= n; i++) scanf("%d", &a[i]);

    for(int i = 0; i <= 26; i++) p[i] = 1<<i;

    for(int i = 0; i <= 24; i++)

        if(cal(i)) ans += 1<<i;

    printf("%d", ans);

}

这样的时间复杂度是$O(n \log n \log C)$，假如我们不用二分排序而是基数排序的话，我能把复杂度降至$O(n \log C)$

E.Instant Noodles

题意：

在一个$2n$个节点，$m$条边的二分图中，右边部分每个节点有一个权值

构建一个左边节点的子集$S$，所有和这些子集有边的右边节点构成点集$N(S)$，$N(S)$的所有节点权值和为$F(S)$

求所有$F(S)$的最大公约数

思路：

首先我们观察发现可以进行缩点

给右边点分类，如果两个点的边集相同，那么他们属于一类

边集相同的意思是，他们所连接的左边节点的数量和类型一模一样属于相同类的节点权值相加

如下图所示：

→

其实$F(S)$所包含的点我们可以用维恩图来表示：

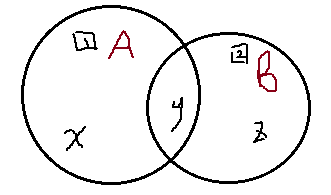
我们要求的答案便是$gcd(A, B, A\bigcup B )$，但是最终我们可以转化成$gcd(x, y, z)$.

因为$gcd$有下列性质 $gcd(a, b, c)=gcd(a, gcd(b,c))$ and $gca(a+b, a)=gcd(a+b, b)=gcd(a, b)$

利用这些性质和数学归纳法，很容易能把这个推向$N(S)$（子集个数）更多时候的情况，即最后求所有权值的最大公因数

这里我们可以直接用$vector$进行$hash$：

#include <cstdio>

#include <cstring>

#include <algorithm>

#include <vector>

#include <map>

#define ll long long

#define pb push_back

using namespace std;

const int maxn = 5e5+100;

int T, n, m, u, v;

ll c[maxn];

vector<int> g[maxn];

ll gcd(ll a, ll b){

    return b ? gcd(b, a%b) : a;

}

int main(){

    scanf("%d", &T);

    while(T--){

        scanf("%d%d", &n, &m);

        for(int i = 1; i <= n; i++){

            scanf("%lld", &c[i]);

            g[i].clear();

        }

        for(int i = 1; i <= m; i++){

            scanf("%d%d", &u, &v);

            g[v].pb(u);

        }

        map<vector<int>, ll> mp;

        for(int i = 1; i <= n; i++){

            if(!g[i].size()) continue;

            sort(g[i].begin(), g[i].end());

            mp[g[i]] += c[i];

        }

        ll ans = 0;

        for(auto i : mp)

            ans = gcd(ans, i.second);

        printf("%lld\n", ans);

    }

}

//Isipired by AC__hunter

也可以选择合适的哈希函数，这里提供一种，至于为什么正确我也不知道

将$1-maxn$每一位的数字对应一个数（$e.g. 1331^i$）那么这串$vector$就$hash$为所有数字的对应值之和

Refence:

https://codeforces.ml/blog/entry/74148

https://www.cnblogs.com/FrankChen831X/p/12442160.html?utm_source=tuicool

https://www.cnblogs.com/carcar/p/12442211.html

https://www.cnblogs.com/lilibuxiangtle/p/12436420.html

https://www.cnblogs.com/Kanoon/p/12464330.html