matlab数字图像简单的加密方法

图像加密的重要性可想而知，每个人都会有自己的小秘密，通过图像加密的方法可以保护自己的照片等的安全。

一般情况下，图像加密可以分为以下几个步骤：

1.选择图像加密算法

2.根据算法获取秘钥

3.根据保存的秘钥解密

图像加密的处理方式多为对图像中的像素点进行处理，有的处理方式不改变灰度直方图的信息（易破解），然后更高级的处理方式使得原来的灰度直方图信息也发生改变（比如变得均衡化了）。

下面介绍自己亲自测试的2种图像加密算法：

1.行列像素点置乱方法，该方法将原图中的像素信息进行了重新排布——置乱。通过一一对应的关系可以恢复原来的图像，此时的秘钥即为行列变换的映射向量Mchange和Nchange。

简单的MATLAB程序如下：

clc,clear all,close all
Lena = imread('Lena512.bmp');
figure;imshow(Lena)
title('原图')
[M,N]   = size(Lena);
Rm      = randsample(M,M)';
Mchange = [1:1:M;Rm];
Rn      = randsample(N,N)';
Nchange = [1:1:N;Rn];

%打乱行顺序
Lena (Mchange(1,:),:) = Lena (Mchange(2,:),:);
figure;imshow(Lena)
title('行加密后图像')
%打乱列顺序
Lena (:,Nchange(1,:)) = Lena (:,Nchange(2,:));
figure;imshow(Lena)
title('列加密后图像')
%列变换还原
Lena (:,Nchange(2,:)) = Lena (:,Nchange(1,:));
figure;imshow(Lena)
title('列解密后图像')
%行变换还原
Lena (Mchange(2,:),:) = Lena (Mchange(1,:),:);
figure;imshow(Lena)
title('解密后图像')

2.基于混沌的图像加密方法，产生2个Logistic混沌序列，改造2个Logistic,得到两个y序列，由yl和y2序列对原图像进行值替代加密。秘钥为混沌系统的初始状态值。

可参考的MATLAB程序如下：

%加密方法，混沌序列
clc,clear all,close all
A=imread('Lena512.bmp'); 
imshow(A); title('原图') 
[M,N]=size(A);%原始图像A的尺寸一MxN 
u1=4;u2=4;x1(1)=0.2;x2(1)=0.7; 
sumA=sum(sum(A));  
k=mod(sumA,256)*1.0/255; 
x1(1)=(x1(1)+k)/2; x2(1)=(x2(1)+k)/2;  
y1(1)=(1/3.1415926)*asin(sqrt(x1(1))); 
y2(1)=(1/3.1415926)*asin(sqrt(x2(1)));  
for i=1:1:M*N-1 %产生2个Logistic混沌序列   
    x1(i+1)=u1*x1(i)*(1-x1(i));   
    x2(i+1)=u2*x2(i)*(1-x2(i)); 
end
for i=1:1:M*N  %改造2个Logistic,得到两个y序列
      y1(i)=(1/3.1415926)*asin(sqrt(x1(i)));   
      y2(i)=(1/3.1415926)*asin(sqrt(x2(i))); 
end
n=1;  
for i=1:1:M   %由yl和y2序列对原图像进行值替代加密     
    for j=1:1:N        
        if mod(n,1)==0           
            k(n)=mod(floor(y1(n)*10^15),256);       
        else
            k(n)=mod(floor(y2(n)*10^15),256);       
        end
        A1(i,j)=bitxor(A(i,j),k(n));  %得到加密像素      
        n=n+1;     
    end
end
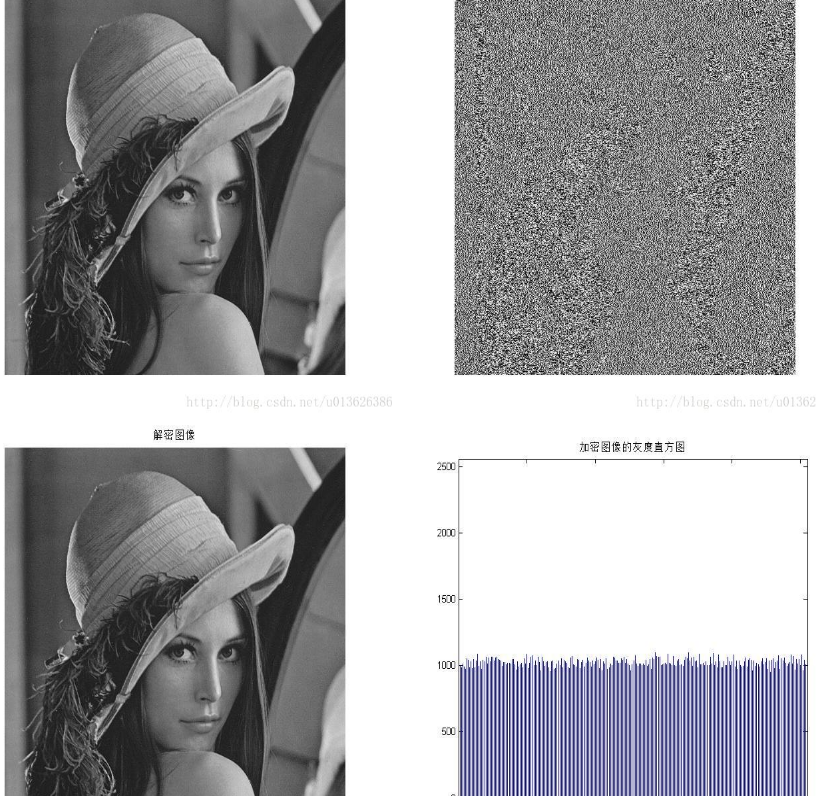
figure,imshow(A1);title('混沌加密图像')  %输出得到的加密图像 
n=1;  
for i=1:1:M     
    for j=1:1:N          
        if mod(n,1)==0             
            k(n)=mod(floor(y1(n)*10^15),256);         
        else
            k(n)=mod(floor(y2(n)*10^15),256);         
        end
        A2(i,j)=bitxor(A1(i,j),k(n));  %得到加密像素      
        n=n+1;     
    end
end
figure,imshow(A2);title('解密图像')  %输出得到的解密图像

---------------------
作者：清风徐行
来源：CSDN
原文：https://blog.csdn.net/u013626386/article/details/39736611
版权声明：本文为博主原创文章，转载请附上博文链接！