狄利克雷卷积 & 莫比乌斯反演

积性函数与完全积性函数

积性函数

若一个数论函数\(f\)满足当\(gcd(n,m)=1\)时，\(f(nm)=f(n)f(m)\)

则称\(f\)为积性函数

一些常见的积性函数

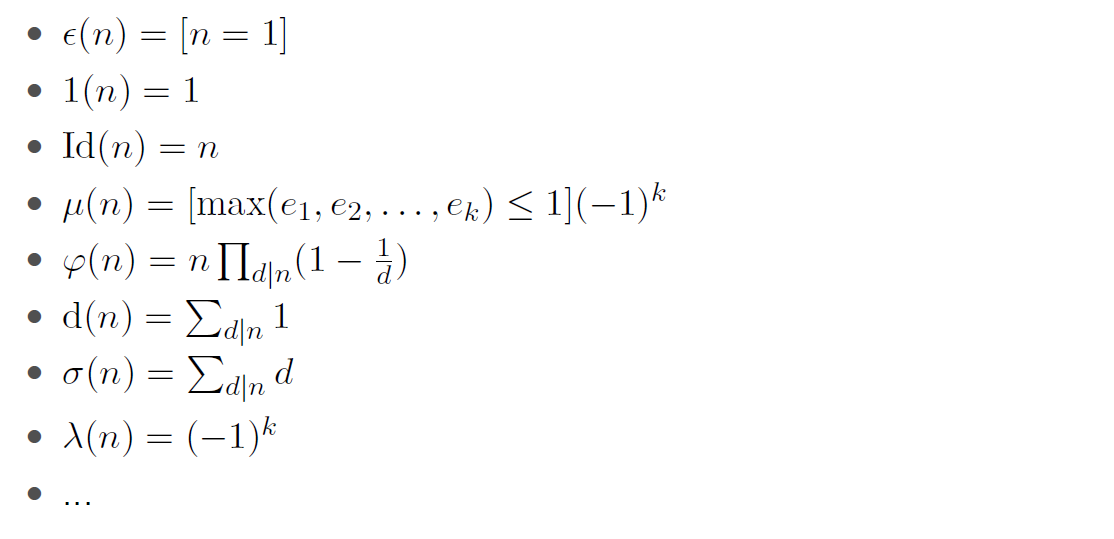
完全积性函数

若一个积性函数函数\(f\)满足当\(gcd(n,m)\ne1\)时，也有\(f(nm)=f(n)f(m)\)

则称\(f\)为完全积性函数

狄利克雷卷积

定义两个数论函数的狄利克雷卷积\(*\)

若\(t=f*g\)

\[t(n)=\sum\limits_{i|n}f(i)g(\frac{n}{i})
\]

等价于

\[t(n)=\sum\limits_{ij=n}f(i)g(j)
\]

狄利克雷卷积有以下性质(两个数论函数相等，是指两个函数的每一项都相等)：

1. 交换律 \(f*g=g*f\)
2. 结合律 \(f*(g*h)=(f*g)*h\)
3. 分配律 \(f*h+g*h=(f+g)*h\)
4. 没有名字\((xf)*g=x(f*g)\)
5. 单位元\(\epsilon*f=f\) ，其中\(\epsilon(n)=[n==1]\)
6. 逆元:对于每一个\(f(1)≠0\)的函数\(f\)，都有\(f∗g=ϵ\)

讨论一下第六个结论，如何求一个函数的逆呢？

只需要定义

\[g(n)=\frac{1}{f(1)}\left([n==1]-\sum\limits_{i|n,i\ne1}f(i)g(\frac{n}{i})\right)
\]

这样的话

\[\sum\limits_{i|n}f(i)g(\frac{n}{i})=f(1)g(n)+\sum\limits_{i|n,i\ne1}f(i)g(\frac{n}{i})=[n==1]
\]

几种比较常见的卷积关系：

\(\mu*1=\epsilon\) 【莫比乌斯反演】【\(\mu\)与\(1\)互为逆元】

\(\varphi*1=Id\)

\(\varphi=Id*\mu\)

\(d=1*1\)

\(1=\mu*d\)

莫比乌斯反演

我们定义\(1\)的逆是\(\mu\)

这样的话，如果\(g=f∗1\)，就有\(f=f∗1∗\mu=g∗\mu\)

换句话说，就是

\[g(n)=\sum\limits_{d|n}f(d)\Leftrightarrow f(n)=\sum\limits_{d|n}\mu(\frac{n}{d})g(d)
\]

也可以这样子

\[g(d)=\sum\limits_{d|n}f(n)\Leftrightarrow f(d)=\sum\limits_{d|n}\mu(\frac{n}{d})*g(n)
\]