martini-新分子的参数化

http://jerkwin.github.io/2016/10/10/Martini%E5%AE%9E%E4%BE%8B%E6%95%99%E7%A8%8BMol/

对新分子的参数化可以分为两种情况，一种是基于已知片段对新分子进行参数化，一种是基于全原子力场模拟对新分子进行参数化。

基于已知片段对新分子进行参数化：为一个含有已知片段, 但尚未被描述过的新分子构建Martini拓扑。

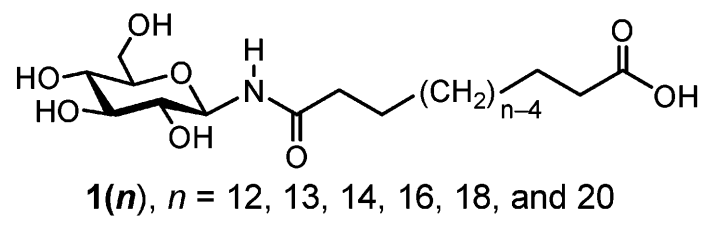
图1 非对称”流星锤”脂分子族, 大亲水端葡萄糖通过烷烃链与小亲水端连接

首先, 将图1中的分子拆分为若干个合理的基本组成单元, 该过程有时会被称为(从原子描述到粗粒级描述的)映射(mapping). 如果你熟悉Martini力场中已有的脂质和蛋白质模型, 并考虑到各个分子片段的化学本性, 那么会很自然地把含有十二烷连接臂的”流星锤”分子粗粒化为8个珠子(图1, n=12时). 你可以通过画图来辅助实现这个想法, 把需要粗粒化成一个珠子的所有原子圈在一起, 并写下珠子类型。我们给将要Martini化的”流星锤”分子起个新名字GDAL(glucose-dodecane-acid-lipid)。

你需要给GDAL写一个拓扑文件, 可以自己从头开始写, 也可以在其他分子拓扑文件的基础上进行改造, GCER分子的拓扑文件就是一个很好的选择. GCER自身只是连接到脂酰基的头基的名字, 如果去检索Martini力场官网提供的脂分子的拓扑文件, 我们会发现一个名为DPGS的带有两条脂肪链尾巴的糖脂分子. 接下来我们将以DPGS的拓扑文件为模板, 其.itp文件部分内容如下:

 1 [ moleculetype ]

 2 DPGS               1

 3 [ atoms ]

 4  1          P4    1    DPGS     C1     1         0        72.0000

 5  2          P1    1    DPGS     C2     2         0        72.0000

 6  3          P1    1    DPGS     C3     3         0        72.0000

 7  4          P1    1    DPGS    AM1     4         0        72.0000

 8  5          P5    1    DPGS    AM2     5         0        72.0000

 9  6          C3    1    DPGS    D1A     6         0        72.0000 ; corrected (C3 instead of C1), oct 2013

10  7          C1    1    DPGS    C2A     7         0        72.0000

11  8          C1    1    DPGS    C3A     8         0        72.0000

12  9          C1    1    DPGS    C4A     9         0        72.0000

13 10          C1    1    DPGS    C1B    10         0        72.0000

14 11          C1    1    DPGS    C2B    11         0        72.0000

15 12          C1    1    DPGS    C3B    12         0        72.0000

16 13          C1    1    DPGS    C4B    13         0        72.0000

根据 1) 其他脂类分子的一般映射规则 2) DPGS分子.itp文件中的成键规则 3) 图2所展示信息, 不难猜测, DPGS分子.itp文件中, 1-3号珠子代表葡萄糖环, 4号珠子代表甘油部分, 5号珠子代表酰胺基团, 其他珠子代表脂肪链尾端. 如果据此编写GDAL分子的.itp文件, 5号珠子应该和3号珠子相连, 而不是与DPGS中一样, 和4号珠子相连, 然后脂肪链尾端(10-13号珠子) 应该与5号珠子相连. 由于GDAL是十二烷连接臂(连接臂占用12/4=3个珠子), 原来的13号珠子应该修改为羧酸末端. 按照上述方式对原DPGS分子的.itp文件进行修改, 我们会发现, 除了13号珠子外, 其他珠子的设定均不用改动. 根据2007年发表的Martini力场论文, 13号珠子应该从C1改为P3类型(论文中P3代表乙酸). 综上所述, GDAL分子.itp文件编写过程如下:

复制一份DPGS分子的.itp文件, 将DPGS替换为GDAL;
去除4, 6, 7, 8, 9号珠子, 将13号珠子的类型从C1修改为P3
把[ bonds ], [ angles ]和[ dihedrals ]中所有涉及4, 6, 7, 8, 9号珠子的条目都删去
对剩余珠子重新进行编号, 即原5号珠子改为4号, 原10号珠子改为5号, 以此类推, 其他成键参数部分会自动保持不变.

如此修改完成后, 仍有一个地方需要修改, 即涉及4号酰胺基团珠子(原5号珠子)的成键参数, 包括环-酰胺的键长, 环-酰胺-烷烃的键角. 这些参数要设为合理值. 酰胺基团整体非常刚性, 因此以其为顶点的键角应接近180°, 且具有高的力常数; 参与成环的珠子与酰胺基团珠子成键的键长可参考蛋白质中骨架粒子-骨架粒子的键长. 你可以从已发表的Martini力场相关论文中查找这些信息.

有了拓扑文件之后, 你还可以直接下载DPGS的坐标文件, 删去4, 6, 7, 8, 9号珠子, 使用它做真空中的能量最小化, 然后利用得到的坐标随机地部分填充空的模拟盒子. 可以再向盒子中添加水分子, 10%的水分子可修改成抗冻水, 然后就可按照脂质教程的步骤进行自组装模拟了.

基于全原子力场模拟对新分子进行参数化

构建过程高度依赖于分子的化学结构以及与其相关的(实验)数据. 我们将使用一个小分子甲苯作为示例分子来讲述该过程. 甲苯的全原子拓扑是已知的, 其水-辛醇分配系数(logP)为2.73(数据来自http://dx.doi.org/10.1021/ci050282s).

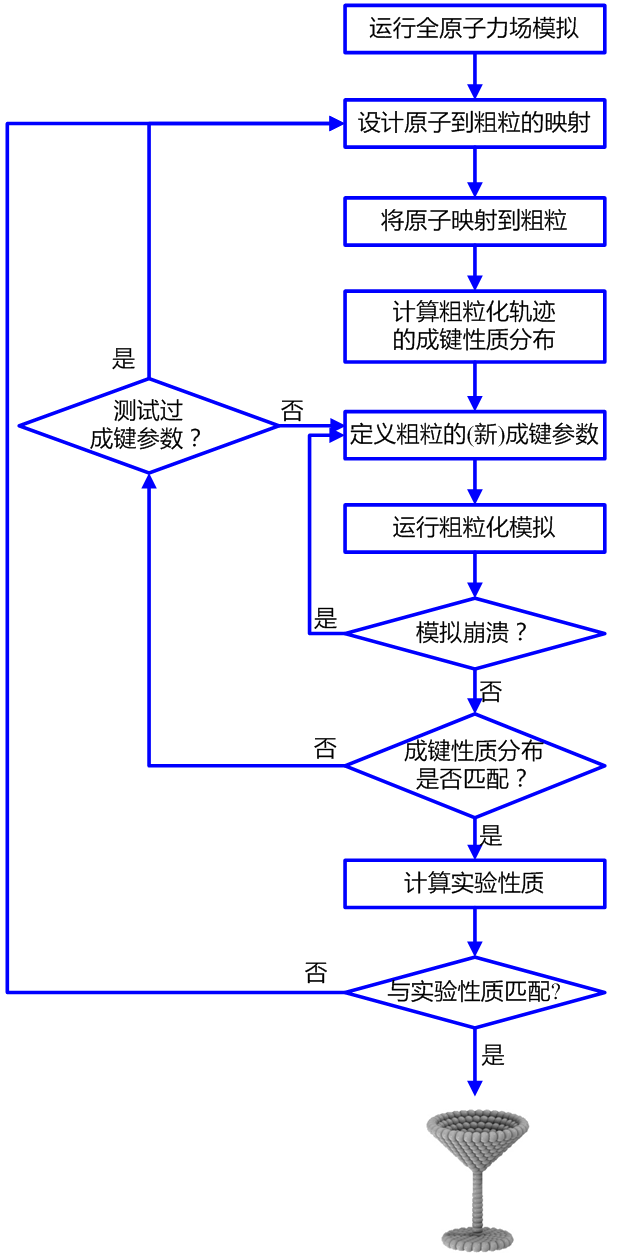
1) 根据全原子力场模拟生成原子的参考数据

对新分子进行可靠的Martini化是基于其在溶液中的全原子力场模拟数据来开展的. 我们自己做Martini化通常基于Gromos力场, 但你也可以自由选择任何力场. 如果没有拓扑文件, 你可以基于ATB或GAFF力场自己来构建一个(这一步的工作量可能也很大)。溶剂的选择很重要: 要Martini化的分子在极性或无极性疏水溶剂中的表现可能会有所不同, 构建的粗粒化模型可能无法两者兼顾. 选择与你做粗粒化模拟时的环境匹配的溶剂, 如果极性和非极性环境都很重要, 那么只能妥协, 选择表现最好的一个.

你可以输入下面的命令进行甲苯的模拟:

1 grompp -f gromos.mdp -c gromos.gro -p gromos.top -o gromos

2 mdrun -v -deffnm gromos

2) 选择原子到粗粒化珠子的映射

此步是粗粒化的核心步骤, 需要依靠你的经验, 化学知识以及不断试错. 推荐的做法是: 把分子结构画在纸上, 复制10次, 然后像小学生画画那样尝试不同的映射方法. 该过程没有规律可循, 但我可以提供一些建议:

你必须使用原始Martini论文表3中的珠子类型, 找到与表3所提供的示例片段相匹配的亚分子结构. 先别考虑键/键角/二面角等问题.
以4个重原子为一组, 对分子结构进行区域划分. 对于平面或环状结构, 或4个重原子分组原则不适用时, 使用S型珠子. 要知道S型珠子与常规珠子相比只是半径小些, 两者的(水-辛烷)相分配自由能是一样的. 举例来说, SC3珠子和C3珠子在P4溶剂(水)中的表现一模一样.
不要使用部分电荷(partial charge). Martini珠子要么带整数电荷, 要么呈电中性(强烈离域化电荷除外, 如金属配体). 如果带电荷, 使用Q类型的珠子.
参考现有的Martini拓扑结构. 你可能需要粗粒化原始Martini论文表3中未提及的亚分子结构, 也许已经有人做过相关工作, 比如蛋白质, 糖类等.
注意分子的对称性, 对同一种亚分子结构使用相同的珠子类型.

3) 对全原子力场模拟轨迹的粗粒化

依据你刚才建立的映射规则, 把在步骤1)中开展的全原子模拟转换为粗粒的模拟. 方法有很多种, 你可以使用转换工具或initram.sh脚本. 不过我认为最简单的方法是, 创建一个GROMACS索引文件, 每一索引组代表一个珠子, 包含该珠子映射原子的编号. 写完索引文件后运行如下命令:

seq 0 2 | g_traj -f gromos.xtc -s gromos.gro -oxt mapped.xtc -n mapping.ndx -com -ng 3

点击下载相应的文件: mapping.ndx

命令中, -ng 3表示索引分组(即珠子个数)有3个, 如果命令前端不加seq 0 2, 你需要挨个输入3个索引分组的名称. 你可以打开我写的索引文件mapping.ndx, 看看是如何对甲苯分子进行映射的.

4) 输出粗粒化轨迹中的键长/键角分布

再去看看你在步骤2)中绘制的映射图, 确定这些珠子之间的成键关系(键, 约束, 键角, 正常和异常二面角). 键长/键角等信息可以从步骤3)中得到的粗粒化轨迹文件(mapped.xtc)中提取. 你可以再制作一个名为bonded.ndx的索引文件, [bonds]下两个珠子一行, [angles]下三个珠子一行, [dihedrals]下四个珠子一行. 使用g_bond来获取键长信息, g_angle来获取键角和二面角信息.

g_bond -f mapped.xtc -n bonded.ndx -noaver -d

g_angle -f mapped.xtc -n bonded.ndx -ov angles.xvg -type angle -all

点击下载相应的文件: bonded.ndx

根据g_angle命令生成的angles.xvg文件可以绘制键角的分布直方图(angles.xvg文件第一列y值是三个键角的平均值, 可舍弃), 你可以使用g_analyze命令:

g_analyze -f angles.xvg -dist angledistr.xvg -bw 1

某些情况下, 仅仅计算键角分布的平均值和标准差就足够了, 然而键角分布可能存在双峰, 最明智的选择是绘制分布图观察下, 可使用xmgrace命令来完成:

xmgrace -nxy -dist angledistr.xvg

一些注意事项: 如果你的分子被周期性边界条件分成两半, 你可能会得到诡异的键长分布结果. 此种情况下, 可首先用trjconv -pbc whole处理一下全原子力场的模拟轨迹, 然后再进行映射. 另一点需要注意的是, 在执行上文中的g_bond命令时, 每条键长的平均值和标准差会存储在bonds.log文件里, 而distance.xvg存储的是所有键长平均后的分布情况. 若想得到每条键长的分布情况, 要么为每一条键单独运行一次g_bond命令, 要么参见后文提供的方法. 一旦你有了CG.tpr文件, 即可在g_bond命令中使用, 从而可以直接比较二者的键长分布.

5) 制作粗粒化分子的`.itp`文件

尽管你可以对已有的.itp文件进行复制粘贴(通常是为了保持文件格式正确), 大部分情况下, 编写.itp文件的工作还是要手动完成的. 你的.itp文件中(可能)将包括以下几项:

[moleculetype]: 一行即可, 包括分子的名字和键合近邻的排除数. Martini力场下, 键合近邻的排除数为1.
[atoms]: 每个珠子一行, 信息包括珠子编号, 珠子类型, 残基编号, 残基名称, 珠子名称, 电荷组编号以及电荷. 对小分子, 残基编号和残基名称和粗粒化之前一样. 珠子名称可自定义. 在Martini力场中, 每个珠子的电荷都有自己的电荷组, 带电量可以为1, 0和-1. 珠子质量已经预定义好了, 在.itp文件中不予注明.
[bonds]: 每条键一行, 信息包括珠子1, 珠子2, 键型、键长和力常数. 在Martini力场中, 键型为1. 键长可采用步骤4)中所获得的平均值. 力常数应该根据键长分布的宽度来调整: 窄峰用大的力常数, 宽峰用小的力常数.
[constraints] [angles] [dihedrals] 正确格式参见GROMACS手册.

6) 创建粗粒化模拟

从mapped.xtc文件中提取出一帧, 使用与全原子模拟相同的溶剂(粗粒化的)癸烷重新溶剂化. 创建一个.top文件(里面应包含Martini力场的.itp文件, 新创建的粗粒化分子的.itp文件, 并添加正确的分子和溶剂个数). 创建一个Martini力场适用的.mdp文件, 可参考官网上的示例. 在正式开始粗粒化模拟之前, 最好先进行能量最小化, 然后用小的时间步长(如5 fs)跑几千步, 让分子弛豫一下. 除此之外, 你还需要.itp文件, .itp文件以及.itp文件. 最好新建一个文件夹来运行粗粒化模拟.

grompp -f em.mdp -c martini.gro -p martini.top -o em

mdrun -v -deffnm em

grompp -f relax.mdp -c em.gro -p martini.top -o relax

mdrun -v -deffnm relax

grompp -f md.mdp -c relax.gro -p martini.top -o md

mdrun -v -deffnm md

点击下载相应的文件: em.mdp, martini.gro, martini.top, relax.mdp, md.mdp

模拟结束后, 重新提取键长和键角. 你仍然可以使用步骤4)中那个索引文件.

g_bond -f md.xtc -s md.tpr -n bonded.ndx -noaverdist -d bonds_martini.xvg

g_angle -f md.xtc -n bonded.ndx -ov angles_martini.xvg -type angle -all

注意和在步骤4)中执行g_bond命令时有什么不同. 这里你使用了-s md.tpr和-noaverdist.

7) 优化CG成键参数

步骤6)可能会有两种结果: 模拟顺利进行, 你得到了键长和键角分布; 模拟崩溃. 如果模拟顺利, 你可以对从步骤6)和步骤4)中获得的分布进行比较, 有必要的话, 回到步骤5)调整.itp中的参数以得到更好的分布. 如果步骤6)中得到的分布峰比较宽, 意味着你需要增大力常数; 如果平均值整体有所偏移, 意味着你需要做相应的回调; 诸如此类. 如果模拟崩溃, 你同样需要返回步骤5), 此行目的是让分子更稳定. 可行的方法有: 减小力常数: 去除不必要的二面角, 将约束(constraint)改变为键或反之. 导致系统不稳定的常见因素有:

如果在4个珠子之间定义了正常二面角(proper dihedral), 且其中3个珠子之间的夹角非常大(接近180°), 这会导致非常严重的波动, 进而导致体系崩溃. 此种情况下, 可取消该二面角, 或使用特殊类型二面角.
如果分子具有环状结构, 粗粒化的珠子可能会连接成三角形. 如果在这些珠子之间设置了约束, LINCS算法可能会失效.
a, b, c三个珠子用既短又弱的键线性连接, b会被a和c排除在外. 如果a, c强烈吸引对方, 其中之一会与b重合.

反复调整直到你对结果满意后, 进入最后一步.

8) 与实验结果比较

两相分配自由能固然是一个好的评估指标(我们目前正在编写一个教程, 主要讲解针对Martini分子如何有效地计算此参数), 但对于纯的液态体系, 密度也可以用来评估. 此外, 任何实验数据都可以用来评估.